[codevs]1250斐波那契数列<矩阵乘法&快速幂>

题目描述 Description

定义：f0=f1=1, fn=fn-1+fn-2(n>=2)。{fi}称为Fibonacci数列。

输入n，求fn mod q。其中1<=q<=30000。

输入描述 Input Description

第一行一个数T(1<=T<=10000)。

以下T行，每行两个数，n，q(n<=109, 1<=q<=30000)

输出描述 Output Description

文件包含T行，每行对应一个答案。

样例输入 Sample Input

3

6 2

7 3

7 11

样例输出 Sample Output

1

0

10

数据范围及提示 Data Size & Hint

1<=T<=10000

n<=109, 1<=q<=30000

感谢：这道题卡了一天，最后发现自己是被坑了，我一直以为斐波那契数列f0=0,f1=f2=1,结果这是f0=f1=1;

　　好吧这只是我智障了，我还是来说说矩阵怎么做吧

　　首先矩阵乘法的定义：

　　　　　　　　　　　　　　　

　　A和B两个矩阵乘出来是

　　　　　　　　　　

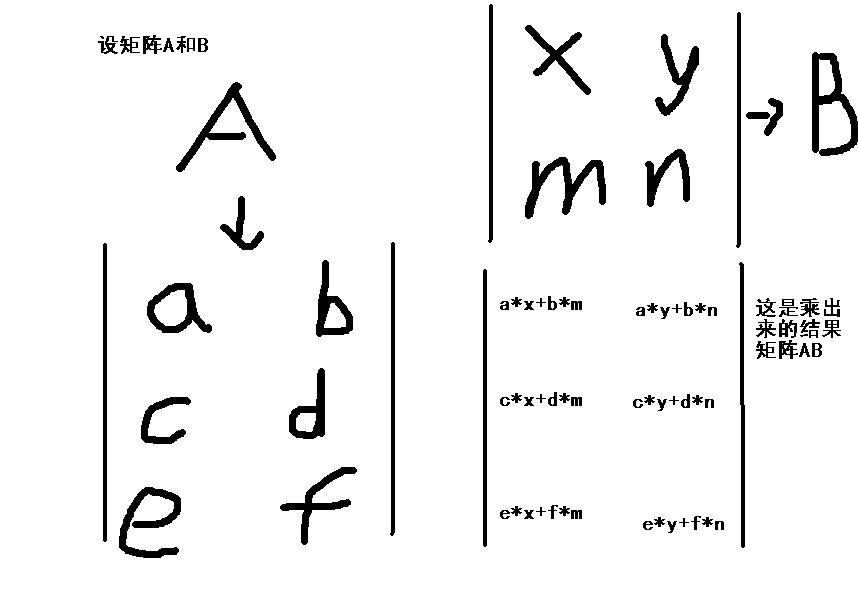
　　知道矩阵是怎么样乘后就可以来解决这道题，我们定义一个初始矩阵和单位矩阵

　　

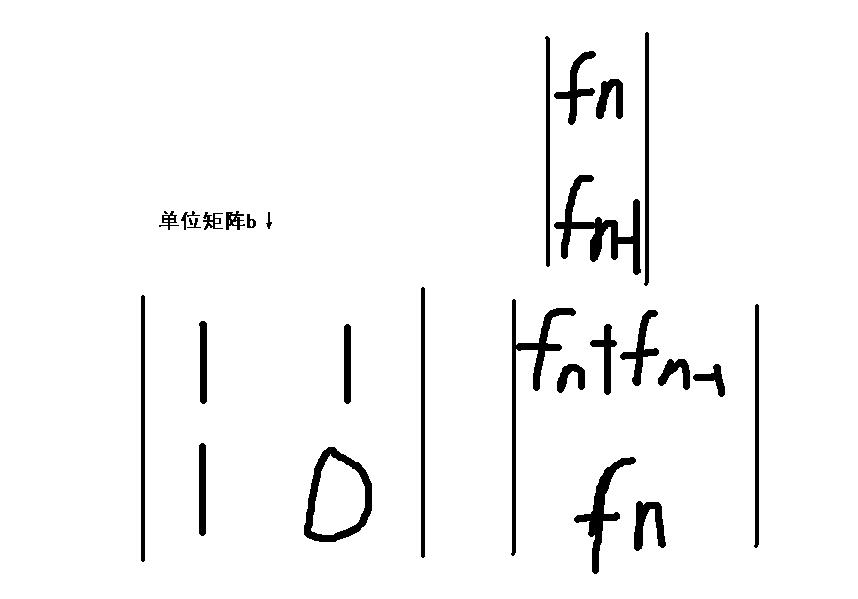
　　而fn+fn-1=fn+1，所以这就是这道题的关键了

　　例如我要求f6 就要用初识矩阵*b^5，而初识矩阵ans[1][1]=f1=1,ans[1][2]=f0=1

　　当数据比较大的时候这个b^n-1次方可能就会爆，所以这又要用到快速幂

　　然后我们来看个快速幂模板

//求a^b %c
void done(int a,int b,int c)
{
    ans=1;
    while(b)
    {
       if(b&)
         ans=(ans*a)%c;
       a=(a*a)%c;
       b>>=;
    }        

}

有了这两个知识，我们就可以实现矩阵快速幂了

　　代码如下：

 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 #include<iostream>
 using namespace std;

 long long  ans[][],c[][],b[][];
 long long n,m,t;

 void dod(int n)
 {
     while(n)
     {
     if(n&)//判断n的奇偶性
     {
         for(int i=;i<=;i++)
          for(int j=;j<=;j++)
          {
              for(int k=;k<=;k++)
              c[i][j]=(c[i][j]+ans[k][j]*b[i][k])%m;//这个地方的i,j，k建议画图分析
          }
         for(int i=;i<=;i++)
           for(int j=;j<=;j++)
          {
              ans[i][j]=c[i][j];
              c[i][j]=;
          }
     }
     for(int i=;i<=;i++)
         for(int j=;j<=;j++)
          {
              for(int k=;k<=;k++)
              c[i][j]=(c[i][j]+b[i][k]*b[k][j])%m;
          }
         for(int i=;i<=;i++)
          for(int j=;j<=;j++)
          {
              b[i][j]=c[i][j];
              c[i][j]=;
          }
     n>>=;

     }

 }

 int main()
 {
     cin>>t;
     while(t--)
     {
         scanf("%lld%lld",&n,&m);
         b[][]=b[][]=b[][]=;
         ans[][]=ans[][]=;
         b[][]=;
         n--;//fn只需要初识矩阵*b^n-1
         dod(n);
         printf("%lld\n",ans[][]%m);
     }

 }

讲题略水，如有错误，望诸位大佬指出