概率图模型之EM算法

一、EM算法概述

EM算法（Expectation Maximization Algorithm，期望极大算法）是一种迭代算法，用于求解含有隐变量的概率模型参数的极大似然估计（MLE）或极大后验概率估计（MAP）。EM算法是一种比较通用的参数估计算法，被广泛用于朴素贝叶斯、GMM（高斯混合模型）、K-means（K均值聚类）和HMM（隐马尔科夫模型）的参数估计。

隐变量是指不能被直接观察到，但是对系统的状态和能被观察到的变量存在影响的变量，比如经典的三硬币模型中，能被观察到的变量是在某次实验中，先后丢两枚硬币的最终结果，比如1或0（1表示正面朝上，0表示背面朝上），而隐变量是第一枚硬币抛掷后的结果（假设是别人抛的，我们不能看到抛第一枚硬币的结果）。用HMM进行词性标注时，可以观察到的变量是词语，而隐变量是每个词的词性。

二、EM算法的迭代步骤

用Y表示可观测随机变量的数据，Z表示隐随机变量的数据，则Y和Z的数据合起来称为完全数据，而单独的观测数据Y称为不完全数据。

给定观测数据Y，θ为需要估计的参数。假设Y和Z的联合概率分布为P(Y, Z|θ)，那么完全数据的对数似然函数是logP(Y, Z|θ)；假设Y的概率分布为P(Y| θ)，那么不完全数据Y的对数似然函数是L(θ)=logP(Y|θ)。

EM算法的目标是什么呢？EM算法的目标是通过迭代，求不完全数据的对数似然函数L(θ)=logP(Y, Z|θ)的极大似然估计，这可以转化为求完全数据的对数似然函数logP(Y, Z|θ)的期望的极大似然估计。

EM算法迭代的步骤如下：

输入：观测变量数据Y，隐变量数据Z，联合分布P(Y, Z|θ)，条件分布P(Z|Y,θ)；

输出：模型参数θ。

1、选择参数的初始值 θ⁽⁰⁾，开始迭代；

2、E步：求期望。记第i次迭代后参数 θ的估计值为θ⁽ⁱ⁾，在第i+1次迭代时，计算完全数据的对数似然函数logP(Y, Z|θ)的期望。

这个期望的完整表述非常长：在给定观测数据Y和第i轮迭代的参数θ⁽ⁱ⁾时，完全数据的对数似然函数logP(Y, Z|θ)的期望，计算期望的概率是隐随机变量数据Z的条件概率分布P(Z|Y, θ⁽ⁱ⁾)。我们把这个期望称为Q函数。

一般我们求期望是用n个样本的概率分布去求，而这里是用隐随机变量数据Z的条件概率分布去求。（在三硬币模型中，这个Z的条件概率分布是抛掷第一枚硬币得到正面或反面的概率：Z∈｛正面，反面｝，P(Z=正面|Y, θ⁽ⁱ⁾)=π，P(Z=反面|Y, θ⁽ⁱ⁾)=1-π。）

3、M步：求极大。求使得Q(θ ,θ⁽ⁱ⁾)极大化的θ，确定第i+1次迭代的参数估计值θ⁽ⁱ⁺¹⁾。

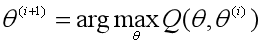
4、重复第2步和第3步，直到收敛而停止迭代。停止迭代的条件是，对于较小的正数ε₁、ε₂，满足：

其中，函数Q(θ ,θ⁽ⁱ⁾)是EM算法的核心，是完全数据的对数似然函数logP(Y, Z|θ)的期望，我们把求不完全数据的对数似然函数L(θ)=logP(Y, Z|θ)的极大似然估计的问题，转化为求Q函数的极大化问题

三、EM算法的推导

（一）Jensen不等式

EM算法的推导需要用到Jensen不等式，一般以凸函数为例来介绍Jensen不等式。

设f(x)是一个定义域在实数集上的函数，如果在x∈R上满足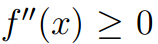，那么称f(x)为凸函数，进一步如果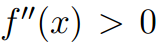对于所有的x都成立，那么f(x)为严格凸函数。假设X是随机变量，那么凸函数的Jensen不等式定义为：

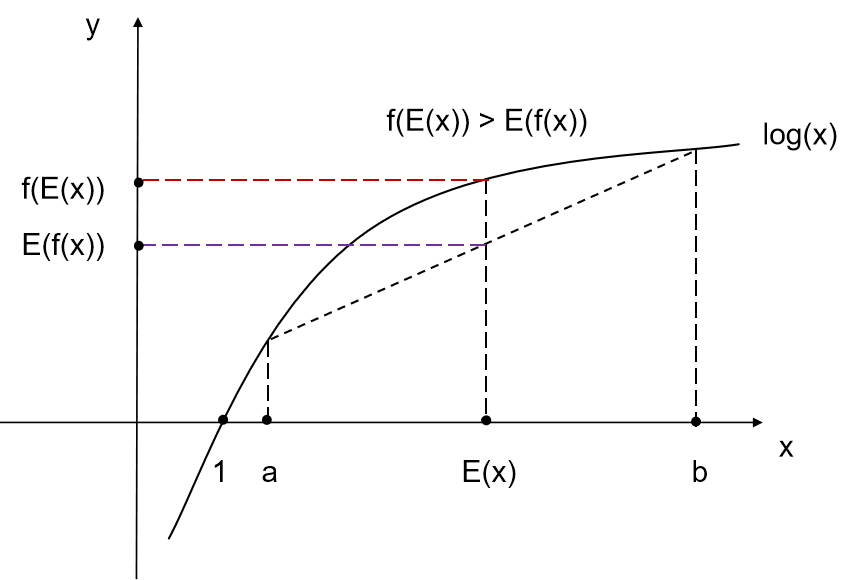
从下图中可以非常直观地理解这个不等式。

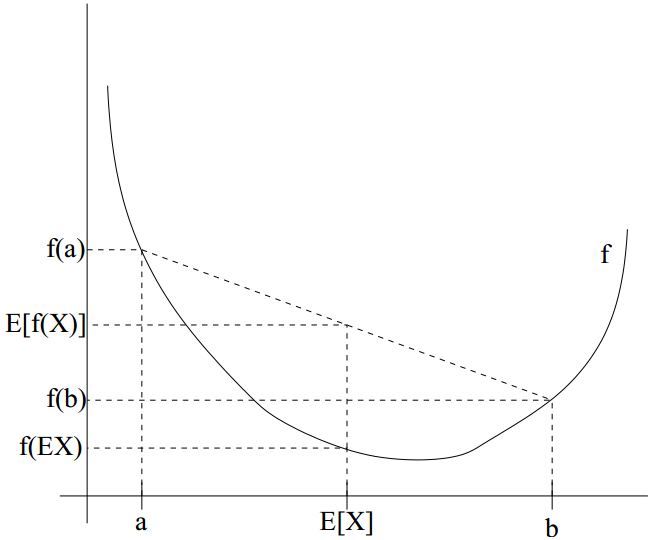
而凹函数的Jensen不等式的不等号方向相反。EM算法中的对数似然函数log(x)的二阶导数为（-1/x²）< 0，底数取自然对数e，那么不等号方向与上面凸函数的相反。EM算法中的Jensen不等式的公式和图如下：

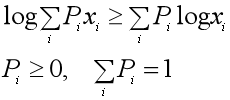
（二） EM算法的推导

EM算法是用Q函数的极大化，来近似实现对不完全数据Y的对数似然函数的极大似然估计，下面我们从不完全数据Y的对数似然函数的极大似然估计问题来导出EM算法。

1、原始目标：对于含有隐变量的概率模型，极大化不完全数据Y关于参数θ的对数似然函数，即极大化：

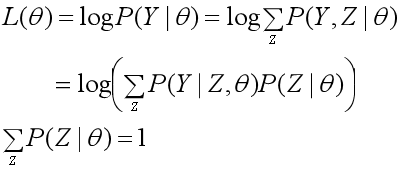
2、假设在第i次迭代后参数θ的估计值是θ⁽ⁱ⁾，EM算法就是让新的估计值θ使L(θ)增加，即L(θ)>L(θ⁽ⁱ⁾)，并逐步逼近极大值。为此，计算二者的差：

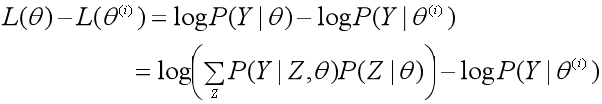
3、用Jensen不等式得到差值的下界：

于是L(θ)的下界为：

4、选择下一个参数θ⁽ⁱ⁺¹⁾，极大化L(θ)的下界B(θ, θ⁽ⁱ⁾)：

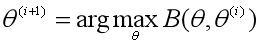
省略掉对参数极大化而言是常数的项，就得到了极大化Q函数Q(θ, θ⁽ⁱ⁾)的表达式：

于是我们得到了第i+1次迭代时的Q函数：

5、不断求解下界的极大化或者说Q函数的极大化，来逼近对数似然函数L(θ)=logP(Y|θ)的极大化。

四、EM算法收敛性的证明

证明EM算法会收敛，其实就是证明不完全数据Y的对数似然函数L(θ)=logP(Y|θ)是单调递增的，即L(θ⁽ⁱ⁺¹⁾) ≥ L(θ⁽ⁱ⁾)，而且有上界，那么必然会收敛到一个值。而P(Y|θ)作为概率的乘积，必然小于1，有上界，所以EM算法的收敛性也就是证明Y的似然函数P(Y|θ)是单调递增的，即P(Y|θ⁽ⁱ⁺¹⁾) ≥ P(Y|θ⁽ⁱ⁾)。于是有以下的证明。

1、定理：设L(θ)=logP(Y|θ)是观测数据Y的对数似然函数，θ⁽ⁱ⁾（i=1,2,...,n）是EM算法得到的参数估计序列，L(θ⁽ⁱ⁾)为对应的对数似然函数序列，则L(θ⁽ⁱ⁾)=logP(Y|θ⁽ⁱ⁾)必定会收敛到某一值L^*。

2、证明思路：只要证明log(x)是单调递增函数（以e为底），且x有上界即可。在EM算法中，P(Y|θ)是有上界的，又log(x)单调递增，因此只要证明P(Y|θ)是单调递增的。

3、证明观测数据Y的似然函数P(Y|θ)是单调递增的，即P(Y|θ⁽ⁱ⁺¹⁾) ≥ P(Y|θ⁽ⁱ⁾)：

由于：

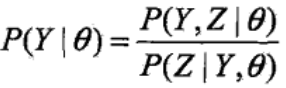
取对数得到：

已知Q函数为：

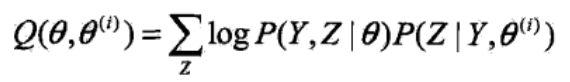
再构造一个H函数：

由：

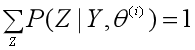
于是对数似然函数可以写成：

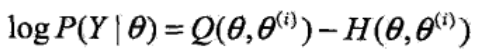
分别取θ为θ⁽ⁱ⁾、θ⁽ⁱ⁺¹⁾，让对数似然函数相减，有：

对于等式右端的第一项，由于θ⁽ⁱ⁺¹⁾是使Q(θ, θ⁽ⁱ⁺¹⁾)达到极大所得到的，所以有：

再看等式右端的第二项，同样运用Jensen不等式：

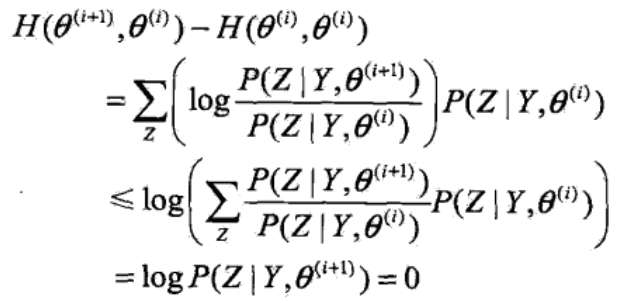
于是得到：

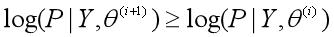
参考资料：

1、李航：《统计学习方法》

2、CS229：《The EM algorithm 》