BZOJ4650 [NOI2016]优秀的拆分【后缀数组】

题目

如果一个字符串可以被拆分为 AABBAABB 的形式，其中 AA 和 BB 是任意非空字符串，则我们称该字符串的这种拆

分是优秀的。例如，对于字符串 aabaabaa，如果令 A=aabA=aab，B=aB=a，我们就找到了这个字符串拆分成 AABBA

ABB 的一种方式。一个字符串可能没有优秀的拆分，也可能存在不止一种优秀的拆分。比如我们令 A=aA=a，B=baa

B=baa，也可以用 AABBAABB 表示出上述字符串；但是，字符串 abaabaa 就没有优秀的拆分。现在给出一个长度为

nn 的字符串 SS，我们需要求出，在它所有子串的所有拆分方式中，优秀拆分的总个数。这里的子串是指字符串

中连续的一段。以下事项需要注意：出现在不同位置的相同子串，我们认为是不同的子串，它们的优秀拆分均会被

记入答案。在一个拆分中，允许出现 A=BA=B。例如 cccc 存在拆分 A=B=cA=B=c。字符串本身也是它的一个子串。

输入格式

每个输入文件包含多组数据。输入文件的第一行只有一个整数 TT，表示数据的组数。保证 1≤T≤101≤T≤10。接

下来 TT 行，每行包含一个仅由英文小写字母构成的字符串 SS，意义如题所述。

输出格式

输出 TT 行，每行包含一个整数，表示字符串 SS 所有子串的所有拆分中，总共有多少个是优秀的拆分。

输入样例

aabbbb

cccccc

aabaabaabaa

bbaabaababaaba

输出样例

提示

我们用 S[i,j]S[i,j] 表示字符串 SS 第 ii 个字符到第 jj 个字符的子串（从 11 开始计数）。第一组数据中，

共有 33 个子串存在优秀的拆分：S[1,4]=aabbS[1,4]=aabb，优秀的拆分为 A=aA=a，B=bB=b；S[3,6]=bbbbS[3,6]

=bbbb，优秀的拆分为 A=bA=b，B=bB=b；S[1,6]=aabbbbS[1,6]=aabbbb，优秀的拆分为 A=aA=a，B=bbB=bb。而剩

下的子串不存在优秀的拆分，所以第一组数据的答案是 33。第二组数据中，有两类，总共 44 个子串存在优秀的

拆分：对于子串 S[1,4]=S[2,5]=S[3,6]=ccccS[1,4]=S[2,5]=S[3,6]=cccc，它们优秀的拆分相同，均为 A=cA=c，

B=cB=c，但由于这些子串位置不同，因此要计算 33 次；对于子串 S[1,6]=ccccccS[1,6]=cccccc，它优秀的拆分

有 22 种：A=cA=c，B=ccB=cc 和 A=ccA=cc，B=cB=c，它们是相同子串的不同拆分，也都要计入答案。所以第二组

数据的答案是 3+2=53+2=5。第三组数据中，S[1,8]S[1,8] 和 S[4,11]S[4,11] 各有 22 种优秀的拆分，其中 S[1

,8]S[1,8] 是问题描述中的例子，所以答案是 2+2=42+2=4。第四组数据中，S[1,4]S[1,4]，S[6,11]S[6,11]，S[7

,12]S[7,12]，S[2,11]S[2,11]，S[1,8]S[1,8] 各有 11 种优秀的拆分，S[3,14]S[3,14] 有 22 种优秀的拆分，

所以答案是 5+2=75+2=7。

题解

我们设$f[i]$为以$i$为结尾的$AA$串的数量

设$g[i]$为以$i$开头的$AA$串的数量

那么

\[ans = \sum\limits_{i = 2}^{n - 2} f[i] * g[i + 1]
\]

所以我们只要找出所有$AA$串即可

根据后缀数组的套路，为找出所有$AA$串，我们枚举$A$的长度$L$，然后每隔$L$设一个监测点，如图：

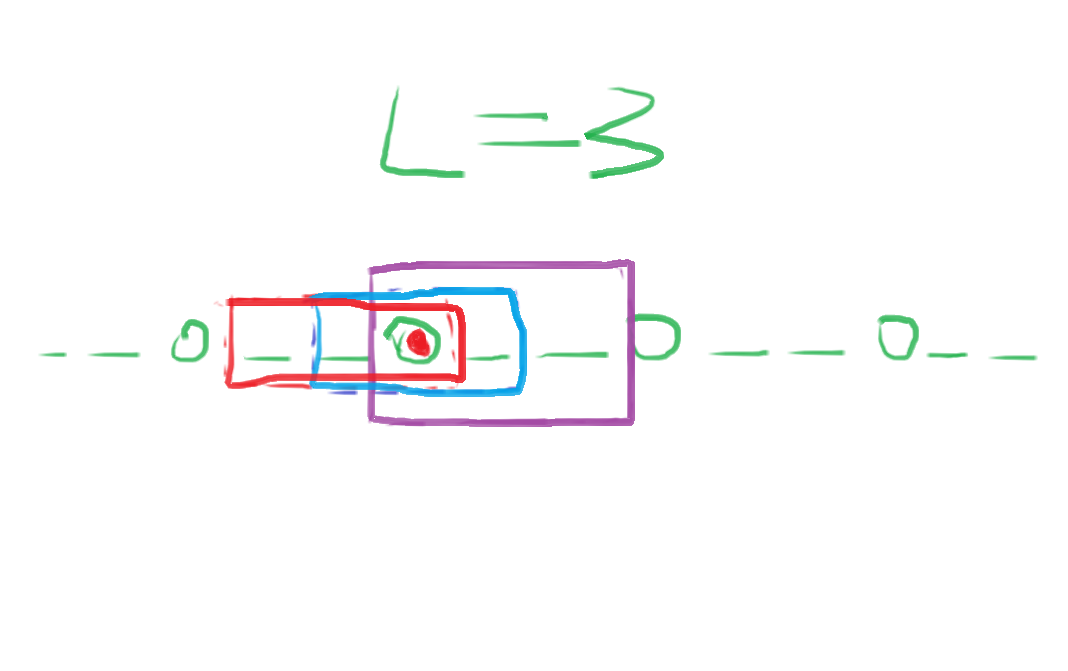
其中圈起来的就是中间那个监测点所管辖的$len = 3$的子串

如此，如果存在长度为$2 * L$的$AA$串，那么相邻的$A$中一定有且仅有一个相邻的监测点

我们就枚举相邻的两个监测点，比较它们的lcp和往前的lcp大小，就可以确定它们管辖的串那些可以匹配

具体对正串反串分别求一次SA【或者并在一起求】，做到$O(1)$询问lcp

然后用一个差分数组维护$f[i]$和$g[i]$

最后统计答案就做完了

时间复杂度$O(nlogn + \sum\limits_{L = 1}^{n} \frac{n}{L}) = O(nlogn + n * \sum\limits_{L = 1}^{n} \frac{1}{L}) = O(nlogn)$

#include<iostream>

#include<cstdio>

#include<cmath>

#include<cstring>

#include<algorithm>

#define LL long long int

#define Redge(u) for (int k = h[u],to; k; k = ed[k].nxt)

#define REP(i,n) for (int i = 1; i <= (n); i++)

#define cls(s) memset(s,0,sizeof(s))

using namespace std;

const int maxn = 100005,maxm = 100005,INF = 1000000000;

inline int read(){

	int out = 0,flag = 1; char c = getchar();

	while (c < 48 || c > 57){if (c == '-') flag = -1; c = getchar();}

	while (c >= 48 && c <= 57){out = (out << 3) + (out << 1) + c - 48; c = getchar();}

	return out * flag;

}

char s[maxn];

int N,n,m,sa[maxn],rank[maxn],height[maxn],t1[maxn],t2[maxn],bac[maxn];

int mn[maxn][18],bin[30],Log[maxn];

void getsa(){

	int *x = t1,*y = t2; m = 1000;

	for (int i = 0; i <= m; i++) bac[i] = 0;

	for (int i = 1; i <= n; i++) bac[x[i] = s[i]]++;

	for (int i = 1; i <= m; i++) bac[i] += bac[i - 1];

	for (int i = n; i; i--) sa[bac[x[i]]--] = i;

	for (int k = 1; k <= n; k <<= 1){

		int p = 0;

		for (int i = n - k + 1; i <= n; i++) y[++p] = i;

		for (int i = 1; i <= n; i++) if (sa[i] - k > 0) y[++p] = sa[i] - k;

		for (int i = 0; i <= m; i++) bac[i] = 0;

		for (int i = 1; i <= n; i++) bac[x[y[i]]]++;

		for (int i = 1; i <= m; i++) bac[i] += bac[i - 1];

		for (int i = n; i; i--) sa[bac[x[y[i]]]--] = y[i];

		swap(x,y);

		x[sa[1]] = p = 1;

		for (int i = 2; i <= n; i++)

			x[sa[i]] = (y[sa[i]] == y[sa[i - 1]] && y[sa[i] + k] == y[sa[i - 1] + k] ? p : ++p);

		if (p >= n) break;

		m = p;

	}

	for (int i = 1; i <= n; i++) rank[sa[i]] = i;

	for (int i = 1,k = 0; i <= n; i++){

		if (k) k--;

		int j = sa[rank[i] - 1];

		while (s[i + k] == s[j + k]) k++;

		height[rank[i]] = k;

	}

	for (int i = 1; i <= n; i++) mn[i][0] = height[i];

	REP(j,17) REP(i,n){

		if (i + bin[j] - 1 > n) break;

		mn[i][j] = min(mn[i][j - 1],mn[i + bin[j - 1]][j - 1]);

	}

}

int lcp(int a,int b){

	int l = rank[a],r = rank[b];

	if (l > r) swap(l,r); l++;

	int t = Log[r - l + 1];

	return min(mn[l][t],mn[r - bin[t] + 1][t]);

}

int pre_lcp(int a,int b){

	int l = rank[N - a + 1],r = rank[N - b + 1];

	if (l > r) swap(l,r); l++;

	int t = Log[r - l + 1];

	return min(mn[l][t],mn[r - bin[t] + 1][t]);

}

LL f[maxn],g[maxn];

void solve(){

	memset(f,0,sizeof(f));

	memset(g,0,sizeof(g));

	for (int L = 1; L <= (n >> 1); L++){

		for (int a = L,b = a + L,l,r,lenl,lenr,len; b <= n; a += L,b += L){

			lenl = min(pre_lcp(a,b),L);

			lenr = min(lcp(a,b),L);

			len = lenl + lenr - 1;

			l = a - lenl + 1; r = l + len - L;

			if (l <= r) g[l]++,g[r + 1]--;

			l = b - lenl + L; r = l + len - L;

			if (l <= r) f[l]++,f[r + 1]--;

		}

	}

	REP(i,n) g[i] += g[i - 1],f[i] += f[i - 1];

	//REP(i,n) printf("%lld",f[i]); puts("");

	//REP(i,n) printf("%lld",g[i]); puts("");

	LL ans = 0;

	for (int i = 2; i < n - 1; i++){

		ans += f[i] * g[i + 1];

	}

	printf("%lld\n",ans);

}

int main(){

	bin[0] = 1; for (int i = 1; i <= 25; i++) bin[i] = bin[i - 1] << 1;

	Log[0] = -1; for (int i = 1; i < maxn; i++) Log[i] = Log[i >> 1] + 1;

	int T = read();

	while (T--){

		cls(s); cls(t1); cls(t2);

		scanf("%s",s + 1); n = strlen(s + 1);

		s[n + 1] = '#';

		for (int i = 1; i <= n; i++) s[n + 1 + i] = s[n - i + 1];

		N = n = n << 1 | 1;

		getsa();

		n >>= 1;

		solve();

	}

	return 0;

}