POJ 3155 Hard Life（最大密度子图+改进算法）

Hard Life

Time Limit: 8000MS		Memory Limit: 65536K
Total Submissions: 9012		Accepted: 2614
Case Time Limit: 2000MS		Special Judge

Description

John is a Chief Executive Officer at a privately owned medium size company. The owner of the company has decided to make his son Scott a manager in the company. John fears that the owner will ultimately give CEO position to Scott if he does well on his new manager position, so he decided to make Scott’s life as hard as possible by carefully selecting the team he is going to manage in the company.

John knows which pairs of his people work poorly in the same team. John introduced a hardness factor of a team — it is a number of pairs of people from this team who work poorly in the same team divided by the total number of people in the team. The larger is the hardness factor, the harder is this team to manage. John wants to find a group of people in the company that are hardest to manage and make it Scott’s team. Please, help him.

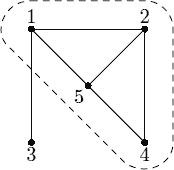
In the example on the picture the hardest team consists of people 1, 2, 4, and 5. Among 4 of them 5 pairs work poorly in the same team, thus hardness factor is equal to ⁵⁄₄. If we add person number 3 to the team then hardness factor decreases to ⁶⁄₅.

Input

The first line of the input file contains two integer numbers n and m (1 ≤ n ≤ 100, 0 ≤ m ≤ 1000). Here n is a total number of people in the company (people are numbered from 1 to n), and m is the number of pairs of people who work poorly in the same team. Next m lines describe those pairs with two integer numbers a_i and b_i (1 ≤ a_i, b_i ≤ n, a_i ≠ b_i) on a line. The order of people in a pair is arbitrary and no pair is listed twice.

Output

Write to the output file an integer number k (1 ≤ k ≤ n) — the number of people in the hardest team, followed by k lines listing people from this team in ascending order. If there are multiple teams with the same hardness factor then write any one.

Sample Input

sample input #1
5 6
1 5
5 4
4 2
2 5
1 2
3 1

sample input #2
4 0

Sample Output

sample output #1
4
1
2
4
5

sample output #2
1
1

Hint

Note, that in the last example any team has hardness factor of zero, and any non-empty list of people is a valid answer.

题目链接：POJ 3155

官方解说在胡伯涛Amber的最小割模型在信息学竞赛中的应用论文中最大密度子图是什么意思呢？就是选出一个子图，使得其子图的${边数 \over 顶点数}$最大，即${|E'| \over |V'|}$最大，后者是不是非常的熟悉，跟01规划非常像，就是使得该比值最大，那么按照01规划的思路，设这个比值为$g$，那么二分出一个$g$的最大值使得$|E'|-g*|V'|>0$，但是我怎么知道$E'$和$V'$怎么取啊？再看式子里面的$E'$和$V'$，可以发现若一条边$e_i$在边集$E'$中，那么$e_i$的两个端点$u_i$与$v_i$必定在顶点集$V'$中，也就是说$e_i$存在的必要条件是$u_i$，$v_i$两点的存在，然后再次观察这个式子，又可以发现可以把边看成新的虚拟点，点还是原来的点，虚拟点的点权为正数1，原来点的点权为负数-g，那么只要在这个新图里求一个最大权闭合图的最大权值就是这个$|E'|-g*|V'|$的最大值即这个式子的最优情况，然后根据其与0（或者叫eps…）的关系进行二分即可，码农题……

代码：

#include <stdio.h>
#include <iostream>
#include <algorithm>
#include <cstdlib>
#include <sstream>
#include <numeric>
#include <cstring>
#include <bitset>
#include <string>
#include <deque>
#include <stack>
#include <cmath>
#include <queue>
#include <set>
#include <map>
using namespace std;
#define INF 0x3f3f3f3f
#define LC(x) (x<<1)
#define RC(x) ((x<<1)+1)
#define MID(x,y) ((x+y)>>1)
#define CLR(arr,val) memset(arr,val,sizeof(arr))
#define FAST_IO ios::sync_with_stdio(false);cin.tie(0);
typedef pair<int, int> pii;
typedef long long LL;
const double PI = acos(-1.0);
const int N = 110;
const int M = 1010;
const double eps = 1e-8;
struct edge
{
    int to, nxt;
    double cap;
    edge() {}
    edge(int _to, int _nxt, double _cap): to(_to), nxt(_nxt), cap(_cap) {}
};
struct info
{
    int u, v;
};
info e[M];
edge E[(N + 3 * M) << 1];
int head[N + M], tot;
int d[N + M];

void init()
{
    CLR(head, -1);
    tot = 0;
}
inline void add(int s, int t, double cap)
{
    E[tot] = edge(t, head[s], cap);
    head[s] = tot++;
    E[tot] = edge(s, head[t], 0);
    head[t] = tot++;
}
int bfs(int s, int t)
{
    queue<int>Q;
    CLR(d, -1);
    d[s] = 0;
    Q.push(s);
    while (!Q.empty())
    {
        int u = Q.front();
        Q.pop();
        for (int i = head[u]; ~i; i = E[i].nxt)
        {
            int v = E[i].to;
            if (d[v] == -1 && E[i].cap > 0)
            {
                d[v] = d[u] + 1;
                if (v == t)
                    return 1;
                Q.push(v);
            }
        }
    }
    return ~d[t];
}
double dfs(int s, int t, double f)
{
    if (s == t || f == 0)
        return f;
    double ret = 0;
    for (int i = head[s]; ~i; i = E[i].nxt)
    {
        int v = E[i].to;
        if (d[v] == d[s] + 1 && E[i].cap > 0)
        {
            double df = dfs(v, t, min(f, E[i].cap));
            if (df > 0)
            {
                E[i].cap -= df;
                E[i ^ 1].cap += df;
                ret += df;
                f -= df;
                if (f == 0)
                    break;
            }
        }
    }
    if (ret == 0)
        d[s] = -1;
    return ret;
}
double dinic(int s, int t)
{
    double ret = 0;
    while (bfs(s, t))
        ret += dfs(s, t, 1e9);
    return ret;
}
double Maxweight(int n, int m, double g)
{
    init();
    int S = 0, T = n + m + 1;
    int i;
    for (i = 1; i <= n; ++i) //负权点连到汇点T
        add(i, T, g);
    for (i = 1; i <= m; ++i) //m个正权点从S连出
    {
        add(S, n + i, 1.0);
        add(n + i, e[i].u, 1e9); //原有边保留
        add(n + i, e[i].v, 1e9);
    }
    return m * 1.0 - dinic(S, T); //正权点-最大流得到最大权
}
int main(void)
{
    int n, m, i;
    while (~scanf("%d%d", &n, &m))
    {
        for (i = 1; i <= m; ++i)
            scanf("%d%d", &e[i].u, &e[i].v);
        if (!m)
        {
            puts("1");
            puts("1");
        }
        else
        {
            double L = 1.0 / n, R = m;
            double ans = 1;
            double dx = 1.0 / n / n;
            while (fabs(R - L) >= dx)
            {
                double mid = (L + R) / 2.0;
                if (fabs(Maxweight(n, m, mid)) >= eps)
                {
                    L = mid;
                    ans = mid;
                }
                else
                    R = mid;
            }
            Maxweight(n, m, ans);
            vector<int>pos;
            for (i = 1; i <= n; ++i)
                if (~d[i])
                    pos.push_back(i);
            int sz = pos.size();
            sort(pos.begin(), pos.end());
            printf("%d\n", sz);
            for (i = 0; i < sz; ++i)
                printf("%d\n", pos[i]);
        }
    }
    return 0;
}

---

改进算法：由论文可得$h(g)={{U*n-c[S, T]} \over 2}$，其中可以令$U=m$，然后新的建图方式为

改进后从600ms到200ms，效果还是不错的

代码：

#include <stdio.h>
#include <iostream>
#include <algorithm>
#include <cstdlib>
#include <sstream>
#include <numeric>
#include <cstring>
#include <bitset>
#include <string>
#include <deque>
#include <stack>
#include <cmath>
#include <queue>
#include <set>
#include <map>
using namespace std;
#define INF 0x3f3f3f3f
#define LC(x) (x<<1)
#define RC(x) ((x<<1)+1)
#define MID(x,y) ((x+y)>>1)
#define CLR(arr,val) memset(arr,val,sizeof(arr))
#define FAST_IO ios::sync_with_stdio(false);cin.tie(0);
typedef pair<int, int> pii;
typedef long long LL;
const double PI = acos(-1.0);
const int N = 110;
const int M = 1010;
const double eps = 1e-8;
struct edge
{
    int to, nxt;
    double cap;
    edge() {}
    edge(int _to, int _nxt, double _cap): to(_to), nxt(_nxt), cap(_cap) {}
};
struct info
{
    int u, v;
};
info e[M];
edge E[(N + M) << 2];
int head[N], tot;
int d[N], deg[N];

void init()
{
    CLR(head, -1);
    tot = 0;
}
inline void add(int s, int t, double cap)
{
    E[tot] = edge(t, head[s], cap);
    head[s] = tot++;
    E[tot] = edge(s, head[t], 0);
    head[t] = tot++;
}
int bfs(int s, int t)
{
    queue<int>Q;
    CLR(d, -1);
    d[s] = 0;
    Q.push(s);
    while (!Q.empty())
    {
        int u = Q.front();
        Q.pop();
        for (int i = head[u]; ~i; i = E[i].nxt)
        {
            int v = E[i].to;
            if (d[v] == -1 && E[i].cap > 0)
            {
                d[v] = d[u] + 1;
                if (v == t)
                    return 1;
                Q.push(v);
            }
        }
    }
    return ~d[t];
}
double dfs(int s, int t, double f)
{
    if (s == t || f == 0)
        return f;
    double ret = 0;
    for (int i = head[s]; ~i; i = E[i].nxt)
    {
        int v = E[i].to;
        if (d[v] == d[s] + 1 && E[i].cap > 0)
        {
            double df = dfs(v, t, min(f, E[i].cap));
            if (df > 0)
            {
                E[i].cap -= df;
                E[i ^ 1].cap += df;
                ret += df;
                f -= df;
                if (f == 0)
                    break;
            }
        }
    }
    if (ret == 0)
        d[s] = -1;
    return ret;
}
double dinic(int s, int t)
{
    double ret = 0;
    while (bfs(s, t))
        ret += dfs(s, t, 1e9);
    return ret;
}
double CST(int n, int m, double g)
{
    init();
    double U = m;
    int S = 0, T = n + 1;
    int i;
    for (i = 1; i <= n; ++i) //<S,v,U>与<v,T,U+2g-dv>
    {
        add(S, i, U);
        add(i, T, U + 2 * g - 1.0 * deg[i]);
    }
    for (i = 1; i <= m; ++i)//(u,v,1)
    {
        add(e[i].u, e[i].v, 1.0);
        add(e[i].v, e[i].u, 1.0);
    }
    return dinic(S, T); //直接计算最小割值（最大流值）
}
int main(void)
{
    int n, m, i;
    while (~scanf("%d%d", &n, &m))
    {
        CLR(deg, 0);
        for (i = 1; i <= m; ++i)
        {
            scanf("%d%d", &e[i].u, &e[i].v);
            ++deg[e[i].u];
            ++deg[e[i].v];
        }
        if (!m)
        {
            puts("1");
            puts("1");
        }
        else
        {
            double L = 1.0 / n, R = m;
            double ans = 1;
            double dx = 1.0 / n / n;
            while (fabs(R - L) >= dx)
            {
                double mid = (L + R) / 2.0;
                double hg = (m * n * 1.0 - CST(n, m, mid)) / 2;
                if (hg >= eps)
                {
                    L = mid;
                    ans = mid;
                }
                else
                    R = mid;
            }
            CST(n, m, ans);
            vector<int>pos;
            for (i = 1; i <= n; ++i)
                if (~d[i])
                    pos.push_back(i);
            int sz = pos.size();
            sort(pos.begin(), pos.end());
            printf("%d\n", sz);
            for (i = 0; i < sz; ++i)
                printf("%d\n", pos[i]);
        }
    }
    return 0;
}