UVA10655 Contemplation! Algebra —— 推公式、矩阵快速幂

题目链接：https://vjudge.net/problem/UVA-10655

题意：

a+b、ab的值分别为p、q，求a^n+b^n。

题解：

1.a、b未知，且直接求出a、b也不太实际。

2.看到 a^n+b^n 这个式子就想到二阶齐次递推式的通项公式，然后就想是否能通过通项公式反推回递推式。结果发现a、b的值是不能确定是否相等的，而求二阶齐次递推式的通项公式时，是需要根据根的情况来分类求解的，所以此题不适应。

3.那么，就直接对 a^n+b^n 做一下变形：

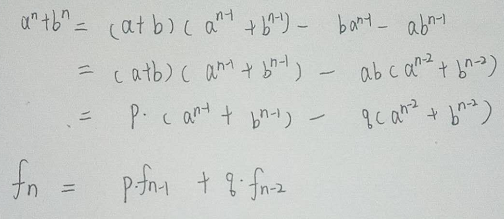
4.得到递推式之后，就直接构造矩阵，然后快速幂。

代码如下：

 #include <iostream>
 #include <cstdio>
 #include <cstring>
 #include <algorithm>
 #include <vector>
 #include <cmath>
 #include <queue>
 #include <stack>
 #include <map>
 #include <string>
 #include <set>
 using namespace std;
 typedef long long LL;
 const int INF = 2e9;
 const LL LNF = 9e18;
 const int MOD = 1e9+;
 const int MAXN = 1e6+;

 const int Size = ;
 struct MA
 {
     LL mat[Size][Size];
     void init()
     {
         for(int i = ; i<Size; i++)
         for(int j = ; j<Size; j++)
             mat[i][j] = (i==j);
     }
 };

 MA mul(MA x, MA y)
 {
     MA ret;
     memset(ret.mat, , sizeof(ret.mat));
     for(int i = ; i<Size; i++)
     for(int j = ; j<Size; j++)
     for(int k = ; k<Size; k++)
         ret.mat[i][j] += 1LL*x.mat[i][k]*y.mat[k][j];
     return ret;
 }

 MA qpow(MA x, LL y)
 {
     MA s;
     s.init();
     while(y)
     {
         if(y&) s = mul(s, x);
         x = mul(x, x);
         y >>= ;
     }
     return s;
 }

 int main()
 {
     LL p, q, n, f[];
     while(scanf("%lld%lld%lld", &p,&q,&n)==)
     {
         f[] = ; f[] = p;
         if(n<=)
         {
             printf("%lld\n", f[n]);
             continue;
         }

         MA s;
         memset(s.mat, , sizeof(s.mat));
         s.mat[][] = p; s.mat[][] = -q;
         s.mat[][] = ; s.mat[][] = ;

         s = qpow(s, n-);
         LL ans = 1LL*s.mat[][]*f[] + 1LL*s.mat[][]*f[];
         printf("%lld\n", ans);
     }
 }