[数据结构]A*寻路算法

简易地图

如图所示简易地图, 其中绿色方块的是起点 (用 A 表示), 中间蓝色的是障碍物, 红色的方块 (用 B 表示) 是目的地. 为了可以用一个二维数组来表示地图, 我们将地图划分成一个个的小方块.

二维数组在游戏中的应用是很多的, 比如贪吃蛇和俄罗斯方块基本原理就是移动方块而已. 而大型游戏的地图, 则是将各种"地貌"铺在这样的小方块上.

寻路步骤

1. 从起点A开始, 把它作为待处理的方格存入一个"开启列表", 开启列表就是一个等待检查方格的列表.

2. 寻找起点A周围可以到达的方格, 将它们放入"开启列表", 并设置它们的"父方格"为A.

3. 从"开启列表"中删除起点 A, 并将起点 A 加入"关闭列表", "关闭列表"中存放的都是不需要再次检查的方格

图中浅绿色描边的方块表示已经加入 "开启列表" 等待检查. 淡蓝色描边的起点 A 表示已经放入 "关闭列表" , 它不需要再执行检查.

从 "开启列表" 中找出相对最靠谱的方块, 什么是最靠谱? 它们通过公式 F=G+H 来计算.

        F = G + H

G 表示从起点 A 移动到网格上指定方格的移动耗费 (可沿斜方向移动).

H 表示从指定的方格移动到终点 B 的预计耗费 (H 有很多计算方法, 这里我们设定只可以上下左右移动).

我们假设横向移动一个格子的耗费为10, 为了便于计算, 沿斜方向移动一个格子耗费是14. 为了更直观的展示如何运算 FGH, 图中方块的左上角数字表示 F, 左下角表示 G, 右下角表示 H. 看看是否跟你心里想的结果一样?

从 "开启列表" 中选择 F 值最低的方格 C (绿色起始方块 A 右边的方块), 然后对它进行如下处理:

4. 把它从 "开启列表" 中删除, 并放到 "关闭列表" 中.

5. 检查它所有相邻并且可以到达 (障碍物和 "关闭列表" 的方格都不考虑) 的方格. 如果这些方格还不在 "开启列表" 里的话, 将它们加入 "开启列表", 计算这些方格的 G, H 和 F 值各是多少, 并设置它们的 "父方格" 为 C.

6. 如果某个相邻方格 D 已经在 "开启列表" 里了, 检查如果用新的路径 (就是经过C 的路径) 到达它的话, G值是否会更低一些, 如果新的G值更低, 那就把它的 "父方格" 改为目前选中的方格 C, 然后重新计算它的 F 值和 G 值 (H 值不需要重新计算, 因为对于每个方块, H 值是不变的). 如果新的 G 值比较高, 就说明经过 C 再到达 D 不是一个明智的选择, 因为它需要更远的路, 这时我们什么也不做.

如图, 我们选中了 C 因为它的 F 值最小, 我们把它从 "开启列表" 中删除, 并把它加入 "关闭列表". 它右边上下三个都是墙, 所以不考虑它们. 它左边是起始方块, 已经加入到 "关闭列表" 了, 也不考虑. 所以它周围的候选方块就只剩下 4 个. 让我们来看看 C 下面的那个格子, 它目前的 G 是14, 如果通过 C 到达它的话, G将会是 10 + 10, 这比 14 要大, 因此我们什么也不做.

然后我们继续从 "开启列表" 中找出 F 值最小的, 但我们发现 C 上面的和下面的同时为 54, 这时怎么办呢? 这时随便取哪一个都行, 比如我们选择了 C 下面的那个方块 D.

D 右边已经右上方的都是墙, 所以不考虑, 但为什么右下角的没有被加进 "开启列表" 呢? 因为如果 C 下面的那块也不可以走, 想要到达 C 右下角的方块就需要从 "方块的角" 走了, 在程序中设置是否允许这样走. (图中的示例不允许这样走)

就这样, 我们从 "开启列表" 找出 F 值最小的, 将它从 "开启列表" 中移掉, 添加到 "关闭列表". 再继续找出它周围可以到达的方块, 如此循环下去...

那么什么时候停止呢? —— 当我们发现 "开始列表" 里出现了目标终点方块的时候, 说明路径已经被找到.

如何找回路径

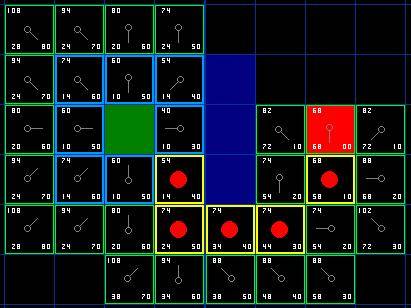
如上图所示, 除了起始方块, 每一个曾经或者现在还在 "开启列表" 里的方块, 它都有一个 "父方块", 通过 "父方块" 可以索引到最初的 "起始方块", 这就是路径.

整个过程抽象

把起始格添加到 "开启列表"
do
{
       寻找开启列表中F值最低的格子, 我们称它为当前格.
       把它切换到关闭列表.
       对当前格相邻的8格中的每一个
          if (它不可通过 || 已经在 "关闭列表" 中)
          {
                什么也不做.
          }
          if (它不在开启列表中)
          {
                把它添加进 "开启列表", 把当前格作为这一格的父节点, 计算这一格的 FGH
          }
          if (它已经在开启列表中)
          {
                if (用G值为参考检查新的路径是否更好, 更低的G值意味着更好的路径)
                    {
                            把这一格的父节点改成当前格, 并且重新计算这一格的 GF 值.
                    }
          }
          目标格已经在 "开启列表", 这时候路径被找到跳出循环；
} while(开启列表不为空)
如果开启列表已经空了,目标格没找到 说明路径不存在.
最后从目标格开始, 沿着每一格的父节点移动直到回到起始格, 这就是路径.

注：这个实现支持斜着走， 如果要实现不支持走沿对角的斜线，可以在此实现的基础上稍作修改即可实现。

代码实现

package com.darrenchan.graph;

import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
import java.util.Scanner;
import java.util.Stack;

public class AStarAlgorithm {

    private static final int[][] DIREC = {{-1, 0}, {-1, 1}, {0, 1}, {1, 1},
            {1, 0}, {1, -1}, {0, -1}, {-1, -1}};

    public static void main(String[] args) {
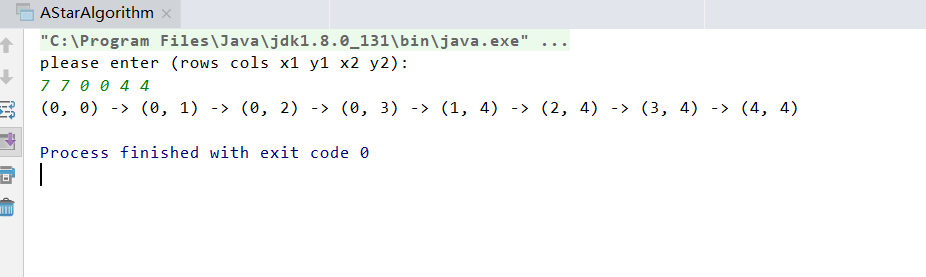
        Scanner scanner = new Scanner(System.in);
        System.out.println("please enter (rows cols x1 y1 x2 y2): ");
        final int rows = scanner.nextInt();
        final int cols = scanner.nextInt();
        int x1 = scanner.nextInt();
        int y1 = scanner.nextInt();
        int x2 = scanner.nextInt();
        int y2 = scanner.nextInt();
        scanner.close();

        // generate a two-dimension array filled with 0
        int map[][] = new int[rows][cols];
        for (int i = 0; i < rows; i++) {
            int tmp[] = new int[cols];
            Arrays.fill(tmp, 0);
            map[i] = tmp;
        }
        int midr = rows / 2;
        int midc = cols / 2;
        /*map[midr - 1][midc] = 1;
        map[midr][midc] = 1;
        map[midr + 1][midc] = 1;*/

        for (int i = 1; i < rows - 1; i++) {
            map[i][midc] = 1;
        }
        map[2][6] = 1;
        map[3][6] = 1;
        map[4][6] = 1;
        map[5][6] = 1;

        findPath(map, x1, y1, x2, y2);
    }

    private static void findPath(int[][] map, int x1, int y1, int x2, int y2) {
        List<Position> openList = new ArrayList<AStarAlgorithm.Position>();//起始列表
        List<Position> closeList = new ArrayList<AStarAlgorithm.Position>();//关闭列表
        boolean findFlag = false;
        Position termPos = null;
        // 起始点
        Position startPos = new Position(x1, y1, calcH(x1, y1, x2, y2));
        openList.add(startPos);//把起始点加入起始列表
        do {
            // 通过在开启列表中找到F值最小的点作为当前点
            Position currentPos = openList.get(0);
            for (int i = 0; i < openList.size(); i++) {
                if (currentPos.F > openList.get(i).F) {
                    currentPos = openList.get(i);
                }
            }
            // 将找到的当前点放到关闭列表中，并从开启列表中删除
            closeList.add(currentPos);
            openList.remove(currentPos);

            //遍历当前点对应的8个相邻点
            for (int i = 0; i < DIREC.length; i++) {
                int tmpX = currentPos.row + DIREC[i][0];
                int tmpY = currentPos.col + DIREC[i][1];
                if (tmpX < 0 || tmpX >= map.length || tmpY < 0 || tmpY >= map[0].length) {
                    continue;
                }
                //创建对应的点
                Position tmpPos = new Position(tmpX, tmpY, calcH(tmpX, tmpY, x2, y2), currentPos);
                //map中对应的格子中的值为1（障碍）， 或对应的点已经在关闭列表中
                if (map[tmpX][tmpY] == 1 || closeList.contains(tmpPos)) {
                    continue;
                }
                //如果不在开启列表中，则加入到开启列表
                if (!openList.contains(tmpPos)) {
                    openList.add(tmpPos);
                } else {
                    // 如果已经存在开启列表中，则用G值考察新的路径是否更好，如果该路径更好，则把父节点改成当前格并从新计算FGH
                    Position prePos = null;
                    for (Position pos : openList) {
                        if (pos.row == tmpX && pos.col == tmpY) {
                            prePos = pos;
                            break;
                        }
                    }
                    if (tmpPos.G < prePos.G) {
                        prePos.setFaPos(currentPos);
                    }
                }
            }
            // 判断终点是否在开启列表中
            for (Position tpos : openList) {
                if (tpos.row == x2 && tpos.col == y2) {
                    termPos = tpos;
                    findFlag = true;
                    break;
                }
            }

        } while(openList.size() != 0);

        if(!findFlag) {
            System.out.println("no valid path!");
            return;
        }

        Stack<String> resStack = new Stack<String>();
        String pattern = "(%d, %d)";
        if (termPos != null) {
            resStack.push(String.format(pattern, termPos.row, termPos.col));
            while(termPos.fa != null) {
                termPos = termPos.fa;
                resStack.push(String.format(pattern, termPos.row, termPos.col));
            }
        }
        StringBuilder sb = new StringBuilder();
        while (!resStack.empty()) {
            sb.append(resStack.pop());
            if (!resStack.empty()) {
                sb.append(" -> ");
            }
        }
        System.out.println(sb.toString());
    }

    /**
     * 计算某个格子的H值
     * @param x
     * @param y
     * @param tx 终点的x值
     * @param ty 终点的y值
     * @return
     */
    private static int calcH(int x, int y, int tx, int ty) {
        int diff = Math.abs(x - tx) + Math.abs(y - ty);
        return diff * 10;
    }

    static class Position {
        public int F;
        public int G;
        public int H;
        public Position fa;
        public int row;
        public int col;

        public Position() {
        }

        public Position(int row, int col, int H) {
            this(row, col, H, null);
        }

        public Position(int row, int col, int H, Position pos) {
            this.H = H;
            this.row = row;
            this.col = col;
            this.fa = pos;
            this.G = calcG();
            this.F = G + H;
        }

        /**
         * 计算某个点到起始点的代价G
         * @return
         */
        private int calcG() {
            if (fa == null) return 0;
            if (fa.row != this.row && fa.col !=  this.col) {
                return 14 + fa.G;
            }
            return 10 + fa.G;
        }

        public void setFaPos(Position pos) {
            this.fa = pos;
            this.G = calcG();
            this.F = G + H;
        }

        @Override
        public boolean equals(Object obj) {
            if (obj == null) {
                return false;
            }
            if (!(obj instanceof Position)) {
                return false;
            }
            Position pos = (Position) obj;
            return this.row == pos.row && this.col == pos.col;
        }

        @Override
        public int hashCode() {
            final int prime = 31;
            int result = 1;
            result = prime * result + row;
            result = prime * result + col;
            return result;
        }

    }

}

参考：

http://www.cnblogs.com/technology/archive/2011/05/26/2058842.html

https://blog.csdn.net/ldstartnow/article/details/51897970