一分钟读懂互联网广告竞价策略GFP+GSP+VCG

原文：http://ju.outofmemory.cn/entry/116780

一分钟读懂互联网广告竞价策略GFP+GSP+VCG

两个广告位，三家广告主竞价，广告平台究竟应该制定广告竞价策略呢？这是本文即将分享的一个问题。

一、前序知识-传统竞价策略
英式拍卖（English Auction）
英式拍卖又叫公开增价拍卖OAB（Open Ascending Bid），卖家提供物品，在物品拍卖过程中，买家按照竞价阶梯由低至高喊价，出价最高者成为竞买的赢家。为了保证竞价收敛，一般会为竞价设定一个终止时间。这种模式非常容易理解，平时电影电视中经常看到。

荷兰式拍卖（Sealed-bid Auction）
荷兰式拍卖亦称公开减价拍卖ODB（Open Descending Bid），其过程与英式拍卖过程相反：竞价由高到低依次递减直到第一个买家应价时成交的一种拍卖方法。

第一价格密封拍卖FPSB（The first-price sealed auction）
第一价格密封拍卖，买方将自己的出价写在一个信封里，众多买方进行投标，同一时间揭晓信封价格，出价最高者竞价成功。

第二价格密封拍卖SPSB（The Second Price Sealed Auction）
又称为维克里拍卖（Vickrey Auction），其拍卖过程和第一价格密封拍卖过程一样，由出价最高的买家获得物品，但他只需要支付所有投标者中的第二高价。

二、核心章节-互联网广告竞价策略
广义第一价格GFP（Generalized First Price）
和传统第一密封竞价类似，出价高者得，需要支付自己提出的报价。
互联网广告竞价（例如搜索广告位竞价）如果按照这种形式竞价，缺点是：
1）平台方收益会非常不稳定；
2）竞价效率不高；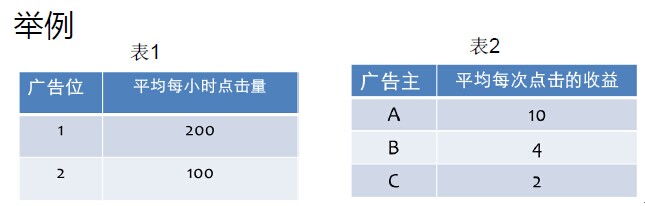

价格的波动：
B -> 2.01（出价超过2，C就会放弃出价）
A-> 2.02
B-> 2.03
A-> 2.04
A和B均会采取“微小差值策略”，直到一方放弃（此例中B会比A先放弃）。
一方放弃之后，另一方失去的竞争者，从而再次把价格拉低（A想，我没有竞争者了，为啥还出价这么高）。
放弃方得知价格被拉低后，又会开始新一轮的“微小差值策略”。

于是，广告位的价格极不稳定，呈现上图中的态势，Yahoo和Google初期都是采用这种策略，直到2002年Google提出了GSP竞价算法。

广义第二价格GSP（Generalized Second Price）
和传统第二密封竞价类似，出价高者得，需要支付出价第二高着提出的报价再加上一个最小值。

此时：
A的实际出价为4+0.01=4.01
B的实际出价为2+0.01=2.01
C竞价失败
GSP是一种稳定的竞价方式，可操作性很强，现阶段几乎所有的互联网广告平台都使用这一种竞价方式。
GSP的不足是，它也不是一种“鼓励讲真话”的机制，说实话不一定形成纳什均衡，竞价的结果不一定全局最优化的。于是，VCG竞价算法出现了。

VCG（Vickrey-Clarke-Groves）竞价机制
广告主为网民的一次点击支付他对其他广告主造成的效用损失。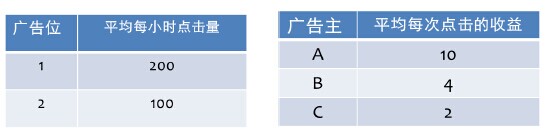

上面的竞价机制描述比较晦涩，举例以说明定价过程：
1）假设A不参加竞价，B和C的社会总效用为200*4 + 100*2 = 1000元
2）A如果参加竞价，B和C的社会总效用为100*4 + 0*2 = 400元
3）因为A参加了竞价，导致B和C的社会总效用损失了1000 – 400 = 600元
4）于是，A需要为每一次点击支付600 / 200 = 3元
但实际应用中，受损者的社会总效用损失难于计算，故VCG竞价机制几乎没有谁真的来使用。

点赞