《Python程序设计（第3版）》[美] 约翰·策勒（John Zelle） 第 1 章 答案

判断对错
1．计算机科学是计算机的研究。
2．CPU 是计算机的“大脑”。
3．辅助存储器也称为 RAM。
4．计算机当前正在处理的所有信息都存储在主存储器中。
5．语言的语法是它的意思，语义是它的形式。
6．函数定义是定义新命令的语句序列。
7．编程环境是指程序员工作的地方。
8．变量用于给一个值赋予一个名称，这样它就可以在其他地方被引用。
9．循环用于跳过程序的一部分。
10．混沌函数不能由计算机计算。
解答

 F（计算机科学不是研究计算机的，其根本问题就是“可以计算 什么”）
 T
 F（RAM是“主存储器”，即随机存取存储器）
 T
 F（语言的语法是它的形式，语义是它的意思）
 T
 F（编程环境是指程序工作的地方）
 T
 F（循环用于让程序重复做同样的事情）
 F（混沌函数是可以计算的，但计算结果可能没有用）

多项选择
1．计算机科学的根本问题是________________。
A．计算机的计算速度有多快
B．可以计算什么
C．什么是有效的编程语言
D．程序员可以赚多少钱

2．算法类似于________________ 。
A．报纸
B．捕蝇草
C．鼓
D．菜谱

3．一个问题是难解的，如果________________。
A．你不能反转其解决方案
B．涉及拖拉机
C．它有很多解决方案
D．解决它不实际

4．以下________________项不是辅助存储器。
A．RAM
B．硬盘驱动器
C．USB 闪存驱动器
D．DVD

5．设计来让人类使用和理解的计算机语言是________________。
A．自然语言
B．高级计算机语言
C．机器语言
D．提取—执行语言

6．语句是________________。
A．机器语言的翻译
B．完整的计算机命令
C．问题的精确描述
D．算法的一部分

7．编译器和解释器之间的一个区别是________________。
A．编译器是一个程序
B．使用编译器将高级语言翻译成机器语言
C．在程序翻译之后不再需要编译器
D．编译器处理源代码

8．按照惯例，程序的语句通常放在一个函数中，该函数名为________________。
A．import
B．main
C．program
D．IDLE

9．关于注释，以下不正确的是________________。
A．它们让程序更有效率
B．它们是为人类读者
C．它们被 Python 忽略
D．在 Python 中，它们以井号（＃）开头

10．函数定义的括号中列出的项被称为________________。
A．括号
B．参数
C．变元
D．B 和 C 项都是正确的
解答

 B
 D
 D
 A
 B
 B
 C
 B
 A
 D

讨论

1、比较并对比本章中的以下概念对。
　　a．硬件与软件
　　b．算法与程序
　　c．编程语言与自然语言
　　d．高级语言与机器语言
　　e．解释器与编译器
　　f．语法与语义
解答

a. 硬件是主体，软件是其灵魂
b. 算法是解决问题的一个秘诀，程序是算法的具体实现
c. 编程语言是计算机使用的、语法及语义都是精确的一门语言，自然语言是人类使用的、充满了模糊和不精确的语言
d. 高级语言是以让人使用和理解为设计目的的语言，机器语言是给计算机硬件理解的一种非常低级的语言
e. 解释器将源代码根据需要一条一条地翻译成机器语言来执行，编译器只需要编译一次，程序就能重复运行
f. 语法是源代码的构成形式，语义是程序想要表达的意思

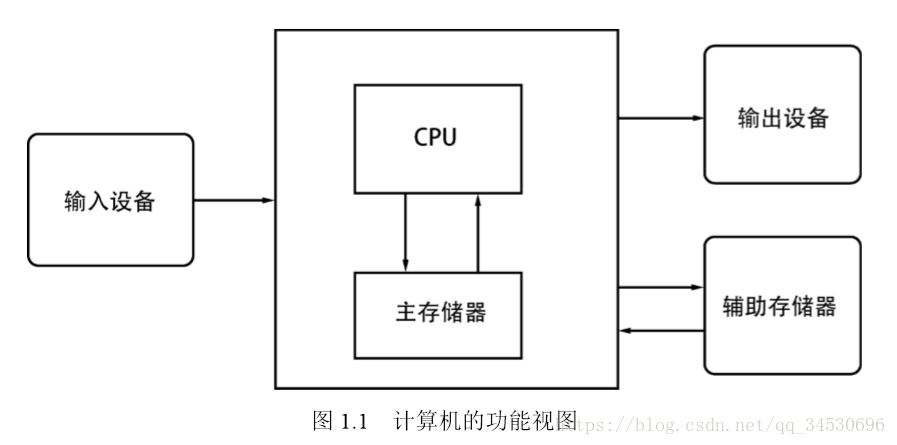
2、列出图 1.1 中计算机的 5 个基本功能单元，并用你自己的话并解释它们的作用。

解答

中央处理单元（CPU）是机器的“大脑”，这是计算机执行所有基本操作的地方。 
主存储器存储程序和数据，但它是易失性存储，当电源关闭时，存储器中的信息会丢失。
辅助存储器提供永久的存储。人类通过输入和输出设备与计算机交互，输入设备允许计算机接收关于世界的信息，
当这些信息经过计算机处理后，输出设备再将新的信息返回给世界让人类吸收。

3、写一个制作花生酱和果冻三明治（或其他日常活动）的详细算法。你应该假设正在与一个概念上能够完成该任务，但从来没有实际做过的人交谈。例如，你可能告诉一个小孩子怎么做。
解答

去商店买花生酱、果冻和面包。
将物品带回家。
在将花生酱罐放入冰箱之前，沿逆时针方向扭转盖子打开花生酱罐。
用勺子搅拌花生酱。
确保不要将油或花生酱洒在罐子外面。
不停搅拌直到罐中的内容物具有均匀的稠度。
把花生酱罐、果冻罐和面包放在冰箱里。
打开冰箱门。
用手抓住花生酱罐把它拿出来。
将您手中拿着的罐子轻轻放在一个平坦的平面上，例如桌子上。
对果冻罐和面包重复这个过程。
关上冰箱门。
打开橱柜。
用手抓住一块盘子。
将盘子从柜子上取下并关闭橱柜门。
将盘子轻轻放在桌子上。
打开餐具所在的抽屉。
用手拿起一把刀。
关上抽屉。
把刀放在桌子上。
是时候打开罐子了。
抓住花生酱罐，如果你是右撇子，用左手牢牢地握住它。
用右手沿逆时针方向旋转罐盖，直到罐盖与罐子完全分开。
如果罐盖没有打开，请带着罐子去厨房水槽。
转动热水旋钮。
等到水很热。
将罐子瓶盖放在流动的热水下。
让热水在罐盖上流动5分钟。
用右手沿逆时针旋方向转罐盖，直到罐盖与罐子完全分开。
对果冻罐重复此过程。
放在桌子上的面包很可能放在塑料袋里。
拿起面包，打开塑料袋。
取出2片不是末端切片的面包。
将切片放在盘子上，并排放置。
把塑料袋合上。
将装有面包的塑料袋放回冰箱里。
拿起刀并握住刀柄。
拿着刀子，将刀刃浸入打开的花生酱罐中。
用刀舀出一些罐子里的东西，使一些花生酱在刀子的刀刃上。
握住刀子，使罐子内容物朝上，然后将刀子从你准备好的两片面包中的一片上移开一英寸。
现在旋转刀具，使其上有罐子内容物的一侧朝下，而不是朝上。
将刀面朝下接触面包的中心，然后轻轻铺展整个切片，使层均匀。
重复此操作，直到面包片上有所需的花生酱稠度。
取下盖子，将其放在罐子顶部，然后沿顺时针方向扭转盖子。
合上花生酱罐。
把罐子放回你找到它的冰箱里。
重复上一段中对于果冻罐的整个过程，把果冻转移到现在有花生酱的切片上。
你将会把果冻涂在花生酱上面。
当你完成果冻时，关闭罐子的方式与关闭罐装花生酱的方法相同。
把罐子放回你找到它的冰箱里。
取上没有任何东西的切片，轻轻地将花生酱和果冻放在切片的顶部，不要将切片挤在一起太硬。
确保两个切片上的角都对齐。
切片的边缘应该是齐平的。
切片本身现在彼此平行，并且在它们之间具有花生酱和果冻。
确保自己清理干净。

请注意，这个问题没有详细说明，因为没有用于定义算法步骤的集合词汇表。换句话说，自然语言对于可靠地描述过程是低效的，甚至对于计算过程也是如此。（例如写这个解答就花了不少时间）

4、

正如你将在后续章节中学到的，存储在计算机中的许多数字不是精确的值，而是接近的近似值。例如，值 0.1 可能存储为 0.10000000000000000555。通常，这样小的差异不是问题。然而，考虑到你在第 1 章中学到的混沌行为，你应该意识到在某些情况下需要谨慎。 你能想到这可能是一个问题的例子吗？请说明。
解答

在任何情况下，为了使计算结果可用，计算结果必须是 100% 准确的，使用浮点型数据类型是不明智的。这种情况的例子：
- 计算测量，尤其是在非常大或者非常小的尺度
- 计算财务价值，尤其是随着时间的推移（例如应计利息）
由于总是发生舍入误差，结果将是不准确的。如果计算以某种像混沌函数一样的方式重复，舍入误差复合，将增加结果的不准确性。

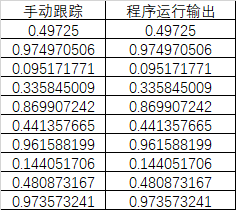
5、使用 0.15 作为输入值，手动追踪第 1.6 节中的 chaos 程序。显示结果的输出序列。

 # File: chaos.py
 # A simple program illustrating chaotic behavior.
 def main():
     print("This program illustrates a chaotic function")
     for i in range(10):
         x = 3.9 * x * (1 - x)
         print(x)
 main() 

解答

x = .15
x = 3.9 * .15 * (1 - .15) = 0.49725
x = 3.9 * 0.49725 * (1 - 0.49725) = 0.97497050625
x = 3.9 * 0.97497050625 * (1 - 0.97497050625) = 0.0951717709512
x = 3.9 * 0.0951717709512 * (1 - 0.0951717709512) = 0.335845009364
x = 3.9 * 0.335845009364 * (1 - 0.335845009364) = 0.869907242293
x = 3.9 * 0.869907242293 * (1 - 0.869907242293) = 0.441357665188
x = 3.9 * 0.441357665188 * (1 - 0.441357665188) = 0.961588198614
x = 3.9 * 0.961588198614* (1 - 0.961588198614) = 0.14405170611
x = 3.9 * 0.14405170611 * (1 - 0.14405170611) = 0.4808731671
x = 3.9 * 0.4808731671 * (1 - 0.4808731671) = 0.973573240627

Python 环境：Python 3.6.4 |Anaconda, Inc.| (default, Jan 16 2018, 10:22:32) [MSC v.1900 64 bit (AMD64)] on win32

编程练习

1、启动交互式 Python 会话，并尝试键入以下每个命令。写下你看到的结果。
解答

>>> print("Hello, world!")
    Hello, world!
>>> print("Hello", "world!")
    Hello world!
>>> print(3)
    3
>>> print(3.0)
    3.0
>>> print(2 + 3)
    5
>>> print(2.0 + 3.0)
    5.0
>>> print("" + "")
    23
>>> print("2 + 3 =", 2 + 3)
    2 + 3 = 5
>>> print(2 * 3)
    6
 >>> print(2 ** 3)
    8
>>> print(7 / 3)
    2.3333333333333335
>>> print(7 // 3)
2 

2、 输入并运行第 1.6 节中的chaos程序。尝试使用各种输入值，观察它在本章中描述 的功能。

解答

3、修改chaos程序，使用 2.0 代替 3.9 作为逻辑函数中的乘数。你修改的代码行应该 像下面这样：

x = 2.0 * x * (1 - x)

用各种输入值运行该程序，并将结果与从原始程序获得的结果进行比较。写一小段话， 描述你在两个版本的行为中观察到的所有差异。
解答

差异：当乘数为 2 时，Logistic 函数的结果似乎表现得"不那么随机"了。

4、修改chaos程序，让它打印出 20 个值，而不是 10 个。
解答
将 range 里的 10 改成 20 即可。

 def main():
     print("This program illustrates a chaotic function")
     x = eval(input("Enter a number between 0 and 1: "))
     for i in range(20):
         x = 3.9 * x * (1 - x)
         print(x)
 main()

5、修改 chaos程序，让打印值的数量由用户确定。你将必须在程序顶部附近添加一行， 从用户获取另一个值：

n = eval(input("How many numbers should I print? ")) 

然后，你需要更改循环，使用 n 代替具体的数字。
解答

 def main():
     print("This program illustrates a chaotic function")
     x = eval(input("Enter a number between 0 and 1: "))
     n = eval(input("How many numbers should I print? "))
     for i in range(n):
         x = 3.9 * x * (1 - x)
         print(x)
 main()

6、在 chaos 程序中执行的计算，可以用代数等价的多种方式来编写。为以下每种计算 方式编写一个程序版本。让你修改的程序打印出 100 次迭代的计算，并比较相同输入的运行结果。

a．3.9 * x * (1 - x)
b．3.9 * (x - x * x)
c．3.9 * x - 3.9 * x * x

 def main ():
     print("This program is an experiment.")
     x = eval(input("Enter a number between 0 and 1: "))
     a = x
     b = x
     c = x
     for i in range(100):
         a = 3.9 * a * (1 - a)
         b = 3.9 * b * (b - b * b)
         c = 3.9 * c - 3.9 * c * c
         print("{0:<30.20}{1:<30.20}{2:<30.20}".format(a, b, c))
 main()

# Output:
This program is an experiment.
Enter a number between 0 and 1: .15
0.4972499999999999698         0.074587500000000001021       0.4972499999999999698
0.97497050625000003521        0.020078537227254493469       0.97497050625000003521
0.095171770951212847356       0.0015407068635790652222      0.095171770951212764089
0.33584500936436861851        9.2434693415137459739e-06     0.33584500936436834095
0.86990724229272164969        3.3321964918918541976e-10     0.8699072422927212056
0.44135766518763547284        4.3303780481818209782e-19     0.44135766518763697164
0.96158819861424271735        7.3133478756682489511e-37     0.96158819861424327247
0.14405170611022782845        2.0859172288711103637e-72     0.14405170611022599658
0.48087316710014554877        1.6969097674235196302e-143    0.48087316710014038623
0.97357324062656191987        1.1230060759231639721e-285    0.97357324062656136476
0.100340704473580275          0.0                           0.10034070447358223177
0.35206254524737101708        0.0                           0.3520625452473771233
0.8896465869771239543         0.0                           0.88964658697713105973
0.38288459530260643415        0.0                           0.3828845953025847848
0.92150752973200633633        0.0                           0.92150752973198646334
0.28209246927896497459        0.0                           0.28209246927903031121
0.78981360141473855307        0.0                           0.78981360141484957538
0.64743149809657429827        0.0                           0.64743149809632338787
0.89022941813909917119        0.0                           0.89022941813938771816
0.38111190475339840056        0.0                           0.38111190475252021415
0.91987592115367633472        0.0                           0.91987592115286209715
0.28744642225787186973        0.0                           0.28744642226053862544
0.79880180869718220293        0.0                           0.79880180870160344409
0.62679816856524084301        0.0                           0.62679816855493664107
0.91229667534915293015        0.0                           0.9122966753593442224
0.31204466083453724634        0.0                           0.31204466080176285203
0.83722388286886373354        0.0                           0.83722388282081494637
0.53149220600910274115        0.0                           0.53149220613548786574
0.97113213974665291151        0.0                           0.97113213971560785609
0.10933457690118721095        0.0                           0.10933457701527249384
0.37978405606059983945        0.0                           0.37978405640823936773
0.91863769460876010253        0.0                           0.91863769493473623751
0.2914956745453838316         0.0                           0.29149567348094995722
0.80545119044019053423        0.0                           0.80545118870906562414
0.61112832400881478279        0.0                           0.61112832813325335124
0.92683693285166823816        0.0                           0.92683692927660099592
0.26445990773974376031        0.0                           0.26445991964231563287
0.75863137325831675462        0.0                           0.75863139512587274282
0.71412826978941723599        0.0                           0.71412822567545441999
0.79618142790026313893        0.0                           0.79618150157941847134
0.63287859089114872901        0.0                           0.63287842067642774424
0.90613879232285265974        0.0                           0.90613896874229937772
0.3316999973450855399         0.0                           0.33169943846887228744
0.86453292551478755357        0.0                           0.86453219185439755812
0.45675141024095838871        0.0                           0.45675349629713180022
0.96770528198703098521        0.0                           0.96770598567816334956
0.12188189988558413568        0.0                           0.1218793327471887622
0.41740413922687186199        0.0                           0.41739656788552631506
0.94839390275426949106        0.0                           0.94838902471134722827
0.19087734109389939419        0.0                           0.19089440182178663008
0.60232840882820803952        0.0                           0.60236954378206664096
0.93416269731207979277        0.0                           0.93412985837282103141
0.23986073382452757774        0.0                           0.23997193766985791541
0.71107749255537822108        0.0                           0.71130308652324369945
0.80124053933248351456        0.0                           0.80086892194042724746
0.62109113610443034137        0.0                           0.62196377806058000814
0.9178140533520593447         0.0                           0.91698686368063930807
0.29418252560393776118        0.0                           0.29687562651935728297
0.80979275220958235604        0.0                           0.81408790670257591415
0.60071095764580806353        0.0                           0.59026026876645643071
0.93544348173925051526        0.0                           0.94322702714060757678
0.23551699942211609673        0.0                           0.2088442294071866101
0.70219009538074428356        0.0                           0.644390437276969541
0.81556474478670948347        0.0                           0.89369046632956550269
0.58663367820602574376        0.0                           0.37053048521271625404
0.94572896262192962524        0.0                           0.90962681448890669866
0.20017019833191598832        0.0                           0.3206029041215163744
0.62439815112354191129        0.0                           0.84948505976242794091
0.91464788998847323942        0.0                           0.49865475271112336131
0.30446179657961724985        0.0                           0.97499294220795396093
0.82588276291220308334        0.0                           0.095088648925262031497
0.56082165686316443054        0.0                           0.3355825113062381182
0.96057283162003592736        0.0                           0.86957086870538313761
0.14770340041665791508        0.0                           0.44232775471695884306
0.49095971309585589859        0.0                           0.96202825728364960156
0.97468126552949407859        0.0                           0.14246656893859155346
0.096243015005739951384       0.0                           0.47646239812648266687
0.3392231585665449467         0.0                           0.97283932706237075116
0.87418814830885838152        0.0                           0.10304958605449687781
0.42893459569423242339        0.0                           0.36047843858712547149
0.95530386241234532818        0.0                           0.89908156221356250182
0.1665237322023604416         0.0                           0.35386223613461131876
0.54129495738145216865        0.0                           0.89171064049245307714
0.96834943332996981091        0.0                           0.37659481908746927914
0.11953035236803503938        0.0                           0.91560752916338761231
0.4104471042001528458         0.0                           0.30135448864054525941
0.94372308753006062254        0.0                           0.82110584718528878412
0.20712830421188160868        0.0                           0.57287503612332990599
0.64048206224414805376        0.0                           0.95428799352909110532
0.89803268173176209466        0.0                           0.17012743384771855659
0.35712293866634492456        0.0                           0.55061795139042390979
0.89538596684416993376        0.0                           0.96500750968844295485
0.36531275516853373153        0.0                           0.13169526214007509779
0.90425144971086368617        0.0                           0.44597131827273472915
0.33766498508599368522        0.0                           0.96361551604817408112
0.87222463743819045323        0.0                           0.13673654778960253608
0.43465039520762988046        0.0                           0.46035469072391865808
0.95834477369857595797        0.0                           0.96887017286437504549
0.15568826685048464675        0.0                           0.11762696789271132047
0.51265277862075009363        0.0                           0.40478437083660567808

当输入值是浮点数据类型时，用代数等价的方式不会返回相同的输出，这是因为浮点数中隐含有舍入错误。

7、（高级）修改chaos程序，让它接受两个输入，然后打印一个包含两列的表，类似 第 1.8 节中显示的表。（注意：你可能无法让列排得与示例中一样好，第 5 章将讨论如何使 用固定小数位数打印数字。
解答

 def main():
     print("Ths program illustrates a chaotic function")
     x = float(input("Enter first number between 0 and 1: "))
     y = float(input("Enter second number between 0 and 1: "))
     z = "input" print("{2:<8}{0:<13.2f}{1:<6.2f}".format(x,y,z))
     print("---------------------------")
     for i in range (10):
         x = 3.9 * x * (1 - x)
         y = 3.9 * y * (1 - x)
         print("{0:>14.6f}{1:>13.6f}".format(x, y))
  main()

# Output:
Ths program illustrates a chaotic function
Enter first number between 0 and 1: .26
Enter second number between 0 and 1: .27
input   0.26         0.27
---------------------------
      0.750360     0.262871
      0.730547     0.276242
      0.767707     0.250260
      0.695499     0.297196
      0.825942     0.201745
      0.560671     0.345666
      0.960644     0.053055
      0.147447     0.176407
      0.490255     0.350698
      0.974630     0.034700