ZZH与计数（矩阵加速，动态规划，记忆化搜索）

题面

因为出题人水平很高，所以这场比赛的题水平都很高。

ZZH 喜欢计数。

ZZH 有很多的数，经过统计，ZZH一共有

v

0

v_0

v0​ 个 0 ，

v

1

v_1

v1​ 个 1，…，

v

2

n

−

1

v_{2^n-1}

v2n−1​ 个

2

n

−

1

2^n-1

2n−1 。因为一些原因，ZZH 只有这

2

n

2^n

2n 种数。

ZZH 和 GVZ 要对这些数进行 m 次操作。每一次操作由一个人进行。每一次，有

p

p

p 的概率由 ZZH 操作，

1

−

p

1 - p

1−p 的概率由 GVZ 操作。

两人进行操作的时候都会依次操作每一个数。对于一个数 s ，如果 ZZH 对这个数进行操作，她会在

0

,

1

,

.

.

.

,

2

n

−

1

0,1,...,2^n-1

0,1,...,2n−1 中找出所有的 t，满足 t or s = s，然后将 s 等概率随机变成找出的 t 中的一个。

如果 GVZ 对这个数进行操作，她会在

0

,

1

,

.

.

.

,

2

n

−

1

0,1,...,2^n-1

0,1,...,2n−1 中找出所有的 t，满足 t and s = s ，然后将等概率随机变成找出的 t 中的一个。（这里的and/or指二进制与/或操作）

因为操作需要非常长的时间，她们想要知道所有操作结束后，对于每一个 i ，i 的个数的期望。因为期望值可能不是整数，所以她们想知道期望值模

998244353

998244353

998244353 的结果。

因为她们觉得这个问题太简单了，于是她们把这个问题交给了你。

输入格式

第一行四个非负整数

n

,

m

,

a

,

b

n,m,a,b

n,m,a,b ，含义同题目，其中

p

=

a

b

p=\frac{a}{b}

p=ba​。

第二行

2

n

2^n

2n 个正整数，表示

v

0

,

v

1

,

.

.

.

,

v

2

n

−

1

v_0,v_1,...,v_{2^n-1}

v0​,v1​,...,v2n−1​。

输出格式

输出一行

2

n

2^{n}

2n 个整数，依次表示 0 的个数的期望，1 的个数的期望，…，

2

n

−

1

2^{n} - 1

2n−1 的个数的期望。

样例

样例输入

2 1 1 3
1 2 3 4

样例输出

665496237 499122178 2 831870299

样例解释

如果 ZZH 进行操作， 0 会随机变为 {0} ，1 会随机变为 {0,1}，2 会随机变为 {0,2,} ，3 会随机变为 {0,1,2,3}。

如果 GVZ 进行操作， 0 会随机变为 {0,1,2,3}，1 会随机变为 {1,3}，2 会随机变为 {2,3} ，3 会随机变为 {3} 。

可以得到期望为

5

3

,

3

2

,

2

,

29

6

\frac{5}{3},\frac{3}{2},2,\frac{29}{6}

35​,23​,2,629​ 。

题解

看到

m

m

m这么大，有手都会想到矩阵快速幂吧。
然后我们想想怎么设计状态。
我们发现，一个数最后变为另一个数的概率只跟里面有多少个1多少个0，以及该数能不能变为那个数有关。

有人想，可以令

d

p

[

i

]

[

j

]

dp[i][j]

dp[i][j] 为原来有

i

i

i 个 1，m 次变化后有

j

j

j 个 1 的概率，
虽然满足第一个限制，即和 1 的数量有关，但是并不一定满足第二个性质，

举个例子：

i
  

:

111110000000000

i\;:111110000000000

i:111110000000000

j
 

:

000000000001111

j\,:000000000001111

j:000000000001111
如果是上面那样定义的 dp 的话，

i

i

i 是可以一次转移到

j

j

j 的，但是根据题意，这合理吗？这不合理。

那么我们得设计一个 dp，使其能够满足那两个限制。

设计 dp

令

d

p

[

z

]

[

x

]

[

y

]

dp[z][x][y]

dp[z][x][y] 为原先有

z

z

z 个 1，最后有

x

x

x 个原先的 0 变为 1，有

y

y

y 个原先的 1 仍是 1（那么自然地，就有

z

−

y

z-y

z−y 个原先的 1 变为 0 了，且不难想到初始状态是

d

p

[

z

]

[

0

]

[

z

]

=

1

dp[z][0][z]=1

dp[z][0][z]=1），

所以这个表我必须得贴出来，以免推到后面大家被搞懵了：

x

:

0

→

1

y

:

1

→

1

z

−

y

:

1

→

0

n

−

z

−

x

:

0

→

0

\begin{matrix} x&:0\rightarrow 1\\ y&:1\rightarrow 1\\ z-y&:1\rightarrow 0\\ n-z-x&:0\rightarrow 0\end{matrix}

xyz−yn−z−x​:0→1:1→1:1→0:0→0​

好了，定义了 dp 以后，我们再想一想它的转移方程，
根据题意，对于

∀

(

t
  

&
  

s

=

=

s

)
  

∥
  

(

t
  

∣
  

s

=

=

s

)

\forall (t\;\&\;s==s)\;\|\;(t\;|\;s==s)

∀(t&s==s)∥(t∣s==s)，t 都对 s 的 dp 状态有贡献，所以状态转移如下：

d

p

[

z

]

[

x

]

[

y

]

=

∑

i

=

x

n

−

z

∑

j

=

y

z

d

p

[

z

]

[

i

]

[

j

]

⋅

p

⋅

2

i

−

x

⋅

2

j

−

y

⋅

2

x

+

y

⋅

C

(

i

,

x

)

⋅

C

(

j

,

y

)

+

∑

i

=

0

x

∑

j

=

0

y

d

p

[

z

]

[

i

]

[

j

]

⋅

(

1

−

p

)

⋅

2

x

−

i

⋅

2

y

−

j

⋅

2

n

−

x

−

y

⋅

C

(

n

−

z

−

i

,

x

−

i

)

⋅

C

(

z

−

j

,

y

−

j

)

\begin{matrix} dp[z][x][y] = \sum_{i=x}^{n-z}\sum_{j=y}^{z}dp[z][i][j]\cdot p\cdot 2^{i-x}\cdot 2^{j-y} \cdot 2^{x+y}\cdot C(i,x) \cdot C(j,y)+\\\sum_{i=0}^{x}\sum_{j=0}^{y}dp[z][i][j]\cdot (1-p)\cdot 2^{x-i}\cdot 2^{y-j} \cdot 2^{n-x-y}\cdot C(n-z-i,x-i) \cdot C(z-j,y-j)\end{matrix}

dp[z][x][y]=∑i=xn−z​∑j=yz​dp[z][i][j]⋅p⋅2i−x⋅2j−y⋅2x+y⋅C(i,x)⋅C(j,y)+∑i=0x​∑j=0y​dp[z][i][j]⋅(1−p)⋅2x−i⋅2y−j⋅2n−x−y⋅C(n−z−i,x−i)⋅C(z−j,y−j)​

然后，是不是就要

n

3

n^3

n3 的状态全部矩阵加速呢？这明显过不了，但是我们会发现

d

p

[

z

]

[

x

]

[

y

]

dp[z][x][y]

dp[z][x][y] 的转移方程里， z 是没有变的，所以，我们可以在外面枚举 z ，在里面把最多

n

2

4

\frac{n^2}{4}

4n2​ 种状态进行矩阵加速（为什么最多这么多种状态呢？因为

x

+

y

<

=

n

x+y<= n

x+y<=n，所以 z 接近

n

2

\frac{n}{2}

2n​ 的时候状态最多），这是可行的。

优化查表

把 dp 处理出来后，我们就处理出了数与数之间转移的概率

但还有个致命的问题，就是计算答案的时候我们还得枚举两个数 i 和 j，然后算上他们的贡献，这是

n

2

n^2

n2 的。

怎么优化呢？
这里的优化是最难讲明白的，我就建个模好了
我们原先实际上是在跑一个图：

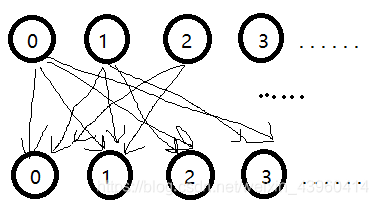
边表示一个数对另一个数的贡献，这样的边有

n

2

n^2

n2 条（有些边权可为 0），所以跑得很慢。

怎么办呢？

第一种理解途径：原理—— “优化建图”

这里说得有点玄乎，实际上是多加一些点，少跑一些边，

我们发现这些边的贡献有重复（这是肯定的吧），于是就可以想一个法子尽量把重复的贡献连向一个中间的工具点，然后再由工具点连向目标点，

上面那句话有点抽象，但是原理很明白，
举个例子，下面 4+4 个点的完全二分图（有向）的所有边权都一样，令边权为 k：

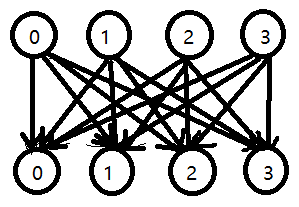
于是我们可以设置一个中间工具点，所有起点连向它，于是它的点权为 4k ，然后它又连向所有终点，给所有终点贡献 4k，这样可以达到原图效果，但是边数却大大减少：

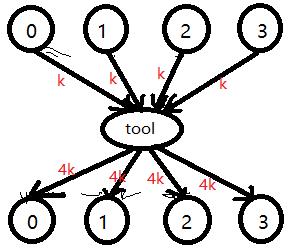
就是这么个原理，所以我们就把计算贡献的图建成这样：

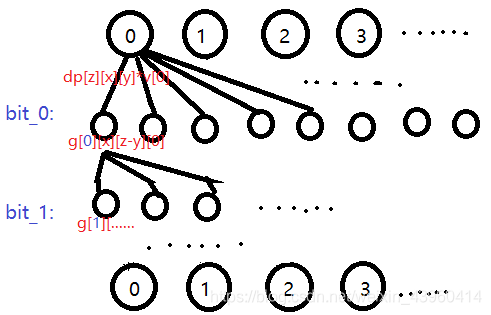
对于其中一个数 i ，我们要使其一位一位地贡献到各个终点去，这样边才最少

第二种理解途径：记忆化搜索

对于 i、j ，换一种枚举方式，先枚举

d

p

[

z

=

b

i

t

c

o

u

n

t

[

i

]

]

[

x

]

[

y

]

dp[z=bitcount[i]][x][y]

dp[z=bitcount[i]][x][y] ，然后这个

d

p

[

z

]

[

x

]

[

y

]

dp[z][x][y]

dp[z][x][y] 就代表着从 i 转移出去，过程中 x 个0变1，z-y 个1变0的所有 j ，i 对 j 的贡献都为

d

p

[

z

]

[

x

]

[

y

]

dp[z][x][y]

dp[z][x][y]；

然后具体有哪些 j 呢？一般的思路是暴力枚，从 i 的第一位开始dfs，枚举这一位要不要变，如果变，0变1的话就消耗了一下 x，1变0就消耗了一下 z-y，如果不变，那就之接到下一位，于是

void dfs(int t,int S,int I,int J) {//枚到哪一位了 , i 变成什么样了 , x还剩多少 , z-y还剩多少
	......
}

虽然这样会超时，但是它提供给了我们一个思路，因为它可以记忆化

重头戏：g[t][s][i][j]

我们设一个

g

[

t

]

[

S

]

[

i

]

[

j

]

g[t][S][i][j]

g[t][S][i][j]，这是我们定义的，引用一下知名博主的定义（有删改）

这个过程不用建图，设

g

[

t

]

[

s

]

[

i

]

[

j

]

g[t][s][i][j]

g[t][s][i][j] 为操作了

t

t

t 次（是对于每个数位的操作），当前得到的数是

s

s

s，还有

i

i

i 个

0

0

0 要变成

1

1

1，还有

j

j

j 个

1

1

1 要变成

0

0

0，初始化就用上面的方法，转移暴力刷表就行了

附个表：

i

:

0

→

1

j

:

1

→

0

\begin{matrix} i&:0\rightarrow 1\\ j&:1\rightarrow 0\\ \end{matrix}

ij​:0→1:1→0​

附上

g

[

t

]

[

s

]

[

i

]

[

j

]

g[t][s][i][j]

g[t][s][i][j] 的转移：

g

[

0

]

[

s

]

[

i

]

[

j

]

=

d

p

[

b

i

t

c

o

u

n

t

(

s

)

]

[

i

]

[

b

i

t

c

o

u

n

t

(

s

)

−

j

]

⋅

v

s

g

[

t

]

[

s

]

[

i

]

[

j

]

=

g

[

t

−

1

]

[

s

]

[

i

]

[

j

]

+

(

s

[

t

]

=

=

1

?
    

g

[

t

−

1

]

[

s
  

x

o

r
  

(

1

<

<

t

−

1

)

]

[

i

+

1

]

[

j

]

:

g

[

t

−

1

]

[

s
  

x

o

r
  

(

1

<

<

t

−

1

)

]

[

i

]

[

j

+

1

]

)

\begin{matrix} g[0][s][i][j]=&dp[bitcount(s)][i][bitcount(s)-j]\cdot v_s\\ g[t][s][i][j]=&g[t-1][s][i][j]+\\ &(s[t]==1?\;\;g[t-1][s\;xor\;(1<<t-1)][i+1][j]:\\ &g[t-1][s\;xor\;(1<<t-1)][i][j+1]) \end{matrix}

g[0][s][i][j]=g[t][s][i][j]=​dp[bitcount(s)][i][bitcount(s)−j]⋅vs​g[t−1][s][i][j]+(s[t]==1?g[t−1][sxor(1<<t−1)][i+1][j]:g[t−1][sxor(1<<t−1)][i][j+1])​

什么意思呢，t 是前 t 位的意思，S是处理到半截的残疾状态，下面是随便的一种转移过程：

t=0： S: 01011001…
t=1： S:1 1011001…
t=2： S:11 011001…
t=3： S:110 11001…

这其实就是上面dfs的过程！

g[t][s][i][j] 的计算

那么最后，一个数 j 收到的贡献可以直接输出

g

[

n

]

[

j

]

[

0

]

[

0

]

g[n][j][0][0]

g[n][j][0][0] 了。

但是如果真这样开数组，空间会爆炸，所以我们要把第一维 t 给滚动掉，或者改变枚举顺序把它消掉。

为了卡常数，我们得先枚举 i（↑），j（↑），然后再枚举 s，数组开成

g

[

i

]

[

j

]

[

s

]

g[i][j][s]

g[i][j][s]。

CODE

#include<queue>
#include<vector>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
#define MAXN 1000005
#define LL long long
#define DB double
#define ENDL putchar('\n')
#define lowbit(x) ((-x)&(x))
#pragma GCC optimize(2)
LL read() {
	LL f = 1,x = 0;char s = getchar();
	while(s < '0' || s > '9') {if(s=='-')f = -f;s = getchar();}
	while(s >= '0' && s <= '9') {x=x*10+(s-'0');s = getchar();}
	return f * x;
}
const int MOD = 998244353;
int qkpow(int a,int b) {
	int res = 1;
	while(b > 0) {
		if(b & 1) res = res *1ll* a % MOD;
		a = a *1ll* a % MOD;b >>= 1;
	}return res;
}
int n,m,i,j,s,o,k,p,p2;
int a[1<<17|5],dp[20][20][20];
int bt[1<<17|5];
int ct[18][18][1<<17|5],c[20][20],invc[20][20],tx,ty,inv[30],pi2[30];
int I(int x,int y) {return x*(ty+1)+y+1;}
struct mat{
	int n,m;
	int s[95][95];
	mat(){n=m=0;memset(s,0,sizeof(s));}
}A,B,C;
mat operator * (mat a,mat b) {
	mat c;c.n=a.n;c.m=b.m;
	for(int i = 1;i <= a.n;i ++) {
		for(int k = 1;k <= a.m;k ++) {
			if(a.s[i][k])
			for(int j = 1;j <= b.m;j ++) {
				(c.s[i][j] += a.s[i][k] *1ll* b.s[k][j] % MOD) %= MOD;
			}
		}
	}
	return c;
}
mat qkpow(mat a,LL b) {
	mat res;res.n = res.m = a.n;
	for(int i = 1;i <= a.n;i ++) res.s[i][i] = 1;
	while(b > 0) {
		if(b & 1) res = res * a;
		a = a * a; b >>= 1;
	}return res;
}
int main() {
//	freopen("counting.in","r",stdin);
//	freopen("counting.out","w",stdout);
	c[0][0] = 1;invc[0][0] = 1;
	inv[0] = inv[1] = 1;
	for(int i = 1;i <= 18;i ++) {
		c[i][0] = c[i][i] = 1;
		invc[i][0] = invc[i][i] = 1;
		for(int j = 1;j < i;j ++) {
			c[i][j] = (c[i-1][j] + c[i-1][j-1]) % MOD;
			invc[i][j] = qkpow(c[i][j],MOD-2);
		}
		if(i-1) inv[i] = (MOD - inv[MOD % i]) *1ll* (MOD/i) % MOD;
	}
	pi2[18] = qkpow(1<<18,MOD-2);
	for(int i = 17;i >= 0;i --) pi2[i] = pi2[i+1] *2ll % MOD;
	n = read();m = read();s = read();o = read();
	p = s *1ll* qkpow(o,MOD-2) % MOD;
	p2 = (1ll+MOD - p) % MOD;
	for(int i = 0;i < (1<<n);i ++) {
		a[i] = read();
		if(i) bt[i] = bt[i-lowbit(i)] + 1;
	}
	for(int i = 0;i <= n;i ++) {
		A=B=mat();
		A.n = 1;
		tx = n-i,ty = i;
		A.m = B.n = B.m = I(tx,ty);
		A.s[1][I(0,i)] = 1;
		for(int xx = 0;xx <= tx;xx ++) {
			for(int yy = 0;yy <= ty;yy ++) {
				for(int xp = 0;xp <= xx;xp ++) {
					for(int yp = 0;yp <= yy;yp ++) {
						(B.s[I(xp,yp)][I(xx,yy)] += p2 *1ll* pi2[xx-xp] % MOD *1ll* pi2[yy-yp] % MOD *1ll* pi2[n-xx-yy] % MOD *1ll* c[n-i-xp][xx-xp] % MOD *1ll* c[i-yp][yy-yp] % MOD) %= MOD;
					}
				}
				for(int xp = xx;xp <= tx;xp ++) {
					for(int yp = yy;yp <= ty;yp ++) {
						(B.s[I(xp,yp)][I(xx,yy)] += p *1ll* pi2[xp-xx] % MOD *1ll* pi2[yp-yy] % MOD *1ll* pi2[xx+yy] % MOD *1ll* c[xp][xx] % MOD *1ll* c[yp][yy] % MOD) %= MOD;
					}
				}
			}
		}
		C = A * qkpow(B,m);
		for(int xx = 0;xx <= tx;xx ++) {
			for(int yy = 0;yy <= ty;yy ++) {
				dp[i][xx][yy] = C.s[1][I(xx,yy)] *1ll* invc[i][yy] % MOD *1ll* invc[n-i][xx] % MOD;
			}
		}
	}
	for(int i = 0;i < (1<<n);i ++) {
		int zz = bt[i];
		for(int xx = 0;xx <= (n-zz);xx ++) {
			for(int yy = 0;yy <= zz;yy ++) {
				ct[xx][zz-yy][i] = dp[zz][xx][yy] *1ll* a[i] % MOD;//ct其实就是g
			}
		}
	}
	for(int t = 0;t < n;t ++) {
		for(int xx = 0;xx <= n;xx ++) {
			for(int yy = 0;yy <= n-xx;yy ++) {
				for(int S = 0;S < (1<<n);S ++) {
					if(!(S & (1<<t))) {
						if(xx > 0) (ct[xx-1][yy][S ^ (1<<t)] += ct[xx][yy][S]) %= MOD;
					}
					if(S & (1<<t)) {
						if(yy > 0) (ct[xx][yy-1][S ^ (1<<t)] += ct[xx][yy][S]) %= MOD;
					}
				}
			}
		}
	}
	for(int i = 0;i < (1<<n);i ++) {
		printf("%d ",ct[0][0][i]);
	}
	return 0;
}