算法竞赛进阶指南0x41并查集

并查集简介

并查集的两类操作：

1. Get 查询任意一个元素是属于哪一个集合。
2. Merge 把两个集合合并在一起。

基本思想：找到代表元。

注意有两种方法：

• 使用一个固定的值（查询方便，但是在合并的时候需要修改大量的值，比较复杂）

• 使用树形结构，这样合并的时候可以直接让一个叫另一个

  eg. f[root1] = root2

---

并查集的路径压缩以及按秩合并

路径压缩：在每一次进行合并的时候，顺便更改每一个节点的值。（均摊复杂度：\(O(logN)\)）

按秩合并：每一次查询的均摊复杂度是\(O(logN)\)。

如果两个一起使用，那么最终的复杂度是线性的。但是正常使用路径压缩就行。

---

使用并查集来维护具传递性的性质

仅仅维护具有传递性：

AcWing237. 程序自动分析

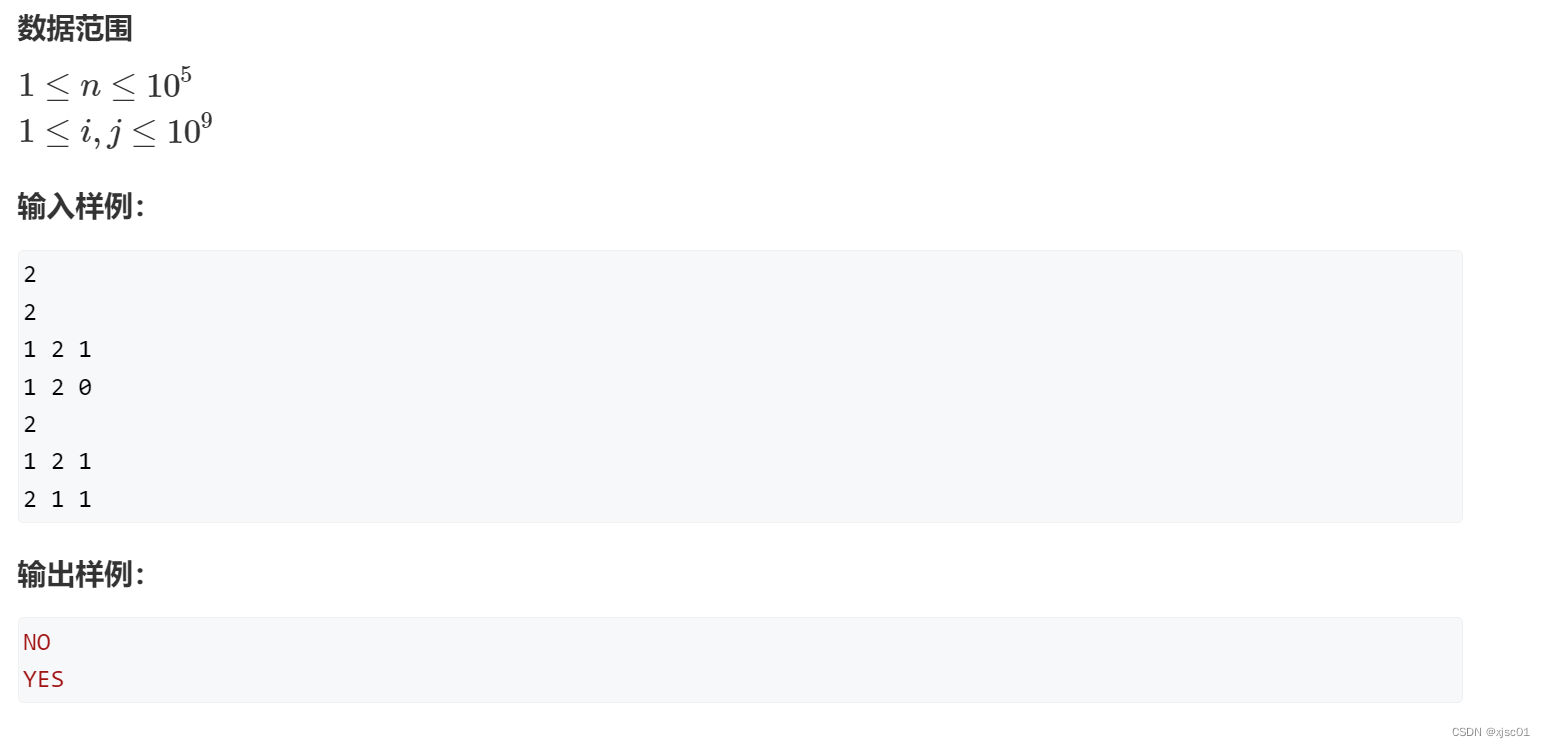
思路：

• 一种方法是使用树的无向图来进行维护相等关系。（每一个块里面全部相等）
• 再就是使用并查集来维护传递关系。
  • 注意：相等具有传递性，但是不相等不具备传递性。

代码：

#include <bits/stdc++.h>
using namespace std;
int fa[200010];
map<int , int >mp;
vector<pair<int, int> >v;
int get(int x)
{
    if(fa[x] == x) return x;
    return fa[x] = get(fa[x]);
}
void solve(int n)
{
    bool tag = true;
    v.clear();
    int cnt = 0;
    for(int i = 1; i <= 2*n; i++) fa[i] = i;
    mp.clear();
    int a, b, eq;
    for(int i = 1; i <= n; i++)
    {
        scanf("%d%d%d", &a, &b, &eq);
        if(mp.find(a) == mp.end())  mp[a] = ++cnt;
        if(mp.find(b) == mp.end())  mp[b] = ++cnt;
        if(eq == 0)
        {
            v.push_back(make_pair(mp[a], mp[b]));
        }
        else
        {
            fa[get(mp[a])] = get(mp[b]);
        }
    }
    for(vector<pair<int, int > >::iterator it = v.begin(); it != v.end(); it++)
    {
        pair<int, int>t = *it;
        if(get(t.first) == get(t.second))
        {
            tag = false;
            break;
        }
    }
    //for(int i = 1; i <= 2*n; i++)
    //{
    //    printf("%d\t%d", i, fa[])
    //}
    if(tag) puts("YES");
    else puts("NO");
}
int main()
{
    int T;
    cin >> T;
    while(T--)
    {
        int n;
        scanf("%d", &n);
        solve(n);
    }
    return 0;
}

---

并查集的带权路径以及扩展域：

• 可以在logN的复杂度内查询某一个节点（在“链”中）到根节点的距离
• 但是也具有要求
  
  在合并的时候，必须是把一个集合全部按照原有的顺序合并到另一个集合的末尾。

这个时候，有两个数组 d 和 size 集合：

1. 如果是根节点，那么就size里存有这一个集合元素的多少。
2. 其他节点存放到父亲节点的带权路径长度d。

注意：仅仅在查询过后，d数组的内容才是到根节点的距离。

---

AcWing238. 银河英雄传说

代码

#include <bits/stdc++.h>
using namespace std;
int fa[30010];
int d[30010];
int s[30010];
int get(int x)
{
    if(x == fa[x]) return x;
    int root = get(fa[x]);
    d[x] += d[fa[x]];
    fa[x] = root;
    return root;
}
int merge(int a, int b)
{
    int x = get(a);
    int y = get(b);
    fa[x] = y;
    d[x] = s[y];
    s[y] += s[x];
}
int main()
{
    int T;
    cin >> T;
    for(int i = 0; i <= 30002; i++)
    {
        fa[i] = i;
        d[i] = 0;
        s[i] = 1;
    }
    while(T--)
    {
        char buf[12];
        int a, b;
        scanf("%s%d%d", buf, &a, &b);
        if(buf[0]=='M')
        {
            if(get(a) != get(b))//如果在一次合并之后，再次合并，那么就是把一个空的合并到了战舰末尾。
                merge(a, b);
        }
        else
        {
            int x = get(a);
            int y = get(b);
            if(x==y)
            {
                if (a==b) puts("0");//注意可能两次询问的是同一个战舰
                else printf("%d\n", abs(d[a]-d[b])-1);
            }
            else
                puts("-1");
        }
    }
    return 0;
}

---

239. 奇偶游戏

思路：

这道题目涉及到区间内的操作。

需要把区间的操作转化为端点的操作。

不妨假设有一个前缀数组，保存着从最开始的点到这一个位置1的个数。

现在进行一下转化：

• 如果一个区间内有奇数个1，那么端点的奇偶性不同。
• 如果一个区间内有偶数个1，那么端点奇偶性相同。

维护一种传递的关系： 使用并查集

注意：区间长度大，但是总体数目少，可以考虑离散化。

方法一：采用带边权来进行实现。

与上一题不同，对于一个抽象的并查集，把一个合并到另一个上时，边权是可以自己给定的。

浅浅地证明一下：当区间端点没有发生冲突，那么存在一种序列满足条件

（为了说明区间端点的冲突是造成判断说谎的充分必要条件）

#include <bits/stdc++.h>
using namespace std;
map<int , int> mp;
int fa[10010];
int d[10010];
//int s[10010];
int get(int x)
{
    if(x == fa[x]) return x;
    int root = get(fa[x]);
    d[x] = d[fa[x]] ^ d[x];
    return fa[x] = root;
}

bool merge(int a, int b, int mod)
{
    int x = get(a);
    int y = get(b);
    if(x==y)
    {
        if(d[a] ^ d[b] == mod)
            return true;
        else
            return false;
    }
    fa[x] = y;
    d[x] = mod^d[a]^d[b];
    return true;
}
int main()
{
    for(int i = 0; i <= 10000; i++)
    {
        fa[i] = i;
        d[i] = 0;
    }
    int ans = INT_MAX;
    int cnt = 0;
    int N, M;
    cin >> N >> M;
    for(int i = 1; i <= M; i++)
    {
        int a, b;
        char buf[12];
        scanf("%d%d%s", &a, &b, buf);
        a--;
        if(mp.find(a) == mp.end()) mp[a] = ++cnt;
        if(mp.find(b) == mp.end()) mp[b] = ++cnt;
        bool tag;
        if(buf[0] == 'e')
            tag = merge(mp[a], mp[b], 0);
        else
            tag = merge(mp[a], mp[b], 1);
        if(!tag)
        {
            ans = min(ans, i);
        }
    }
    if(ans == INT_MAX)
        printf("%d\n", M);
    else
        printf("%d", ans-1);
    return 0;
}

方法二：采用拓展域来进行求解：

还是有一种等价关系，只不过可能由这一个域推到另一个域上。所以，采用多个域来维护传递性。

思路

如果进行查询，没有发现矛盾，直接合并（因为如果本来在一起，合并也没有什么后果）

代码

#include <bits/stdc++.h>
using namespace std;
map<int , int> mp;
int fa[20010];
const int divv = 10002;
int get(int x)
{
    if(x== fa[x]) return x;
    return fa[x] = get(fa[x]);
}
bool merge(int x, int y, int mod)
{
    int x_odd = x;
    int x_even = x + divv;
    int y_odd = y;
    int y_even = y + divv;
    if(mod)//奇数
    {
        if(get(x_odd) == get(y_odd))
        {
            return false;
        }
        else
        {
            fa[get(x_odd)] = get(y_even);
            fa[get(y_odd)] = get(x_even);
        }
    }
    else
    {
        if(get(x_odd) == get(y_even))
            return false;
        else
        {
            fa[get(x_odd)] = get(y_odd);
            fa[get(x_even)] = get(y_even);
        }
    }
    return true;

}
int main()
{
    for(int i = 0; i <= 20009; i++)
    {
        fa[i] = i;
    }
    int ans = INT_MAX;
    int cnt = 0;
    int N, M;
    cin >> N >> M;
    for(int i = 1; i <= M; i++)
    {
        int a, b;
        char buf[12];
        scanf("%d%d%s", &a, &b, buf);
        a--;
        if(mp.find(a) == mp.end()) mp[a] = ++cnt;
        if(mp.find(b) == mp.end()) mp[b] = ++cnt;
        bool tag;
        if(buf[0] == 'e')
            tag = merge(mp[a], mp[b], 0);
        else
            tag = merge(mp[a], mp[b], 1);
        if(!tag)
        {
            ans = min(ans, i);
        }
    }
    if(ans == INT_MAX)
        printf("%d\n", M);
    else
        printf("%d", ans-1);
    return 0;
}

---

AcWing240. 食物链

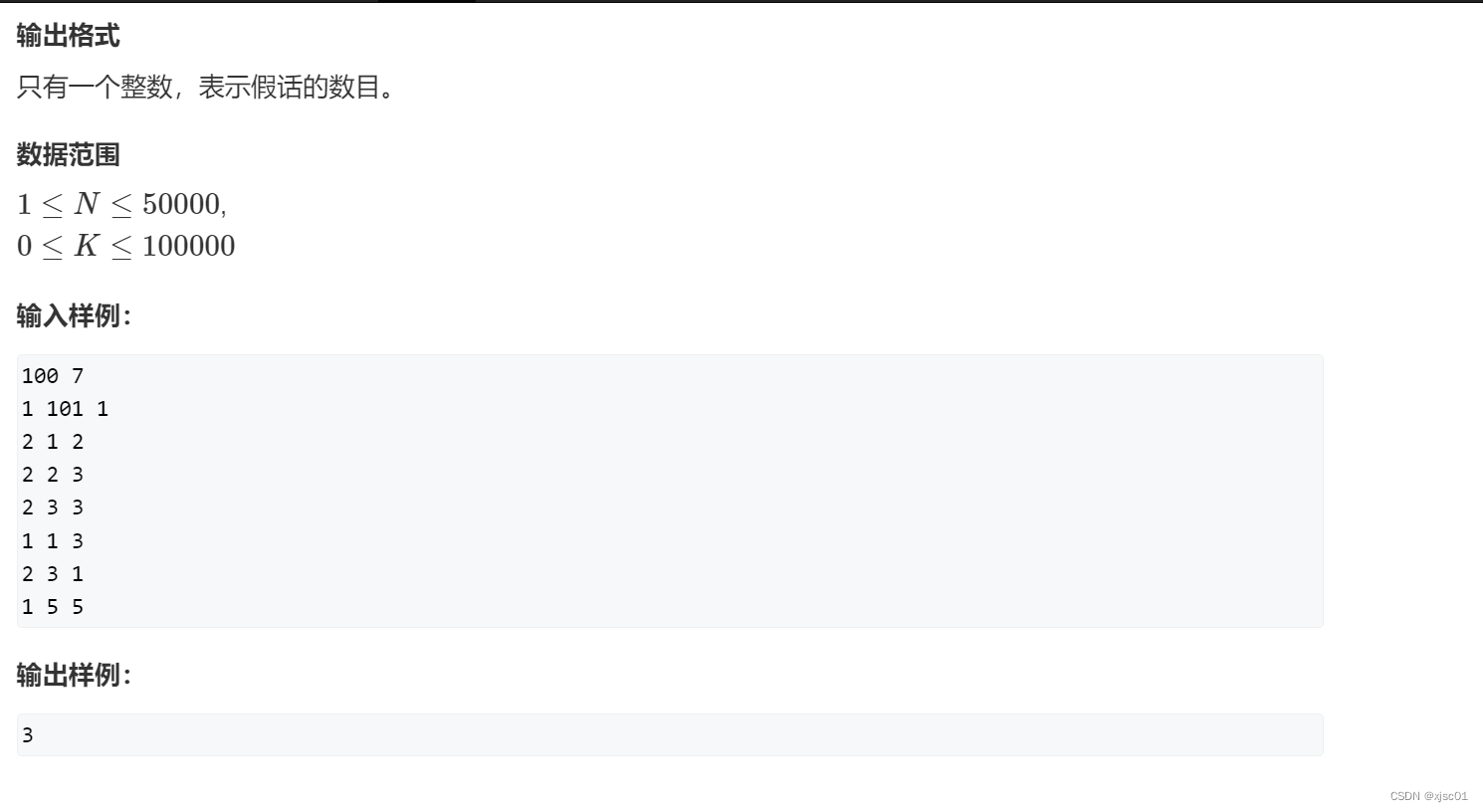
思路：这道题目是要动态地维护传递关系，所以考虑到并查集。

对于这个关系来说，看不出来传递性，所以要使用扩展域或者是边带权。

方法一：扩展域

#include <bits/stdc++.h>
using namespace std;
int fa[150012];
const int divv = 50000;
int get(int x)
{
    if(x == fa[x]) return x;
    return fa[x] = get(fa[x]);
}
bool merge(int tag, int a, int b)
{
    int a1 = a, a2 = a+divv, a3 = a2+divv;
    int b1 = b, b2 = b+divv, b3 = b2 + divv;
    if(tag==1)//表示a与b是同类
    {
        if(get(a1)==get(b2) || get(b1)==get(a2))
            return false;
        fa[get(a1)] = get(b1);
        fa[get(a2)] = get(b2);
        fa[get(a3)] = get(b3);
    }
    else//表示a吃b
    {
        if(get(a1)==get(b1) || get(b1) == get(a2))
            return false;
        fa[get(a1)] = get(b2);
        fa[get(a2)] = get(b3);
        fa[get(a3)] = get(b1);
    }
    return true;
}
int main()
{
    for(int i = 1; i <= 150010; i++)
    {
        fa[i] = i;
    }
    int cnt = 0;
    bool right = true;
    int T, K;
    cin >> T >> K;
    for(int i = 1; i <= K; i++)
    {

        int tag, a, b;
        scanf("%d%d%d", &tag, &a, &b);
        if(a > T || b > T) //针对第二条判断真假
        {
            cnt ++;
            right = false;
        }
        else if(!merge(tag, a, b))//注意：这个必须是else，因为如果
        //上面一旦不合法，那么就不能进行下面的操作
        {
            cnt++;
            right = false;
        }
    }
    printf("%d\n", cnt);
    return 0;
}