「SOL」NOI2016 Day1 解题报告

第一次打 NOI，还是先把以前的 NOI 题刷一遍吧？

---

# 目录

目录

• # 目录
• # A. 优秀的拆分 excellent
• # B. 网格 grid
• # C. 循环之美 cyclic
• # 小结
• # 源代码
• THE END
  • • Thanks for reading!

---

# A. 优秀的拆分 excellent

> Link 优秀的拆分 - LOJ

如果能对每个位置求出以它开头/结尾的形如 AA 的串的数量，那这个问题就非常简单了。

考虑如何对 AA 串计数。和另外一道题（忘了题目了）非常类似，那道题是回文串，将原串 \(kL\) 的位置设为关键点，任何长度为 \(2L\) 的回文串一定经过两个关键点。这道题则是任何 \(|A|=L\) 的 AA 串都会经过两个关键点。

用 SA 快速处理出两个前缀的 LCS 和两个后缀的 LCP。我们可以判断：

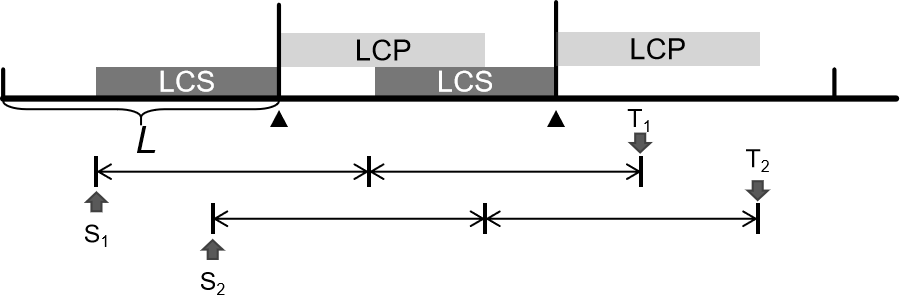
—— 以 \(S_1\) 到 \(S_2\) 这些位置开头存在长度为 \(2L\) 的 AA 串，以 \(T_1\) 到 \(T_2\) 这些位置结尾存在长度为 \(2L\) 的 AA 串。

差分计数即可。

---

# B. 网格 grid

> Link 网格 - LOJ

看来做的题比较多还是有好处。有一类题要求最小化操作数量，看起来非常复杂，但是通过一些人类智慧可以发现最大答案其实很小，即存在简单的合法构造方案。这样将问题转化为「判断是否存在答案为 \(x\) 的可行解」。

（称“跳蚤”为白格，“蛐蛐”为黑格）

同样的道理，分析这道题。首先不难发现无解的情况只有：

• 只有一个白格；
• 只有两个白格且相邻。

排除这两个情况，剩下的都有解。

可以用至多 \(4\) 次操作把一个白格围起来，因此答案至多为 \(4\)。远远不够，我们还发现可以利用一个极大白格连通块的边角处，一个白格连通块必定存在“角”这种只需要两次操作就可以围起来的格子，因此答案至多为 \(2\)。

换句话说，答案只能是 \(0,1,2\)。

答案是 \(0\) 可以直接判断连通性（关于建图之后再分析），那么就只剩下判断答案是 \(1\) 还是 \(2\)。

直观上感觉 \(2\) 比 \(1\) 难判断，的确如此。答案是 \(1\) 意味着只需要填一个格子就可以把原本的连通块割成多个……这不就是割点吗？

可以暴力建出点、边数量都是 \(\mathcal O(nm)\) 的图通过部分数据。

我们只需要用到这张图的连通性以及可能的割点，显然图中有很多点是可以合并的：

• 合并点不会改变原图连通性；
• 如果两个点都不可能是割点，则可以合并，合并后的点不可能是原图的割点。

什么点可能是割点？必然是在周围（八联通）有一个黑格的白格。因此我们只需要把黑格周围的白格单独建点，其他的按行合并。如图：

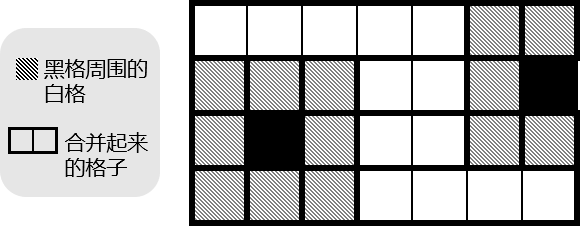
这样点数、边数都与黑格数量同阶，可以用 Tarjan 求割点判断答案，顺便还可以判断连通性。

---

# C. 循环之美 cyclic

久仰大名

结论

一个数 $A$ 是 $k$ 进制 $L$ 纯循环的充要条件是 $A\times k^L-A$ 是整数。

如果 $A$ 表示成最简分数 $\frac xy$，则上述条件等价于 $y\mid k^L-1$。则 $A$ 是 $k$ 进制纯循环小数当且仅当 $k^L\equiv1\pmod y$ 有 $L\gt 1$ 的解 $L$，运用某些数论知识（忘了，但是我记得住结论 awa）可以得到等价条件为 $k,y$ 互质。

于是我们可以知道答案为：

\[\sum_{x=1}^n\sum_{y=1}^m\big[(x,y)=1\big]\big[(y,k)=1\big]
\]

看着就很莫比乌斯反演，但是我自己做的时候思路错了，不应该直接把两个条件都反演掉（只能做到 \(\mathcal O(n\sigma_0(k))\)）……

UPD. 两个条件都反演掉也能做，将 \([(y,k)=1]\) 反演后设 \(t\mid (y,k)\)，则 \(y\) 的可取值的数量为 \(\lfloor\tfrac m{\mathrm{lcm}(t,d)}\rfloor\)，再对 lcm 进行反演：

\[\begin{aligned}
&\sum_{d=1}^n\mu(d)\lfloor\tfrac nd\rfloor\sum_{d\mid j}^{j\le m}[(j,k)=1]\\
=&\sum_d\mu(d)\lfloor\tfrac nd\rfloor\sum_{d\mid j}\sum_{t\mid k,t\mid j}\mu(t)\\
=&\sum_d\mu(d)\lfloor\tfrac nd\rfloor\sum_{t\mid k}\lfloor\tfrac m{\mathrm{lcm}(t,d)}\rfloor\\
\end{aligned}
\]

枚举 \(t,d\) 的 GCD 为 \(p\)：

\[\sum_d\mu(d)\lfloor\tfrac nd\rfloor\sum_{t\mid k}\sum_p\lfloor\tfrac {mp}{td}\rfloor\big[(t,d)=p\big]
\]

再反演掉，第二行是转为枚举 \(r=qp\)：

\[\begin{aligned}
&\sum_d\mu(d)\lfloor\tfrac nd\rfloor\sum_{t\mid k}\sum_p\lfloor\tfrac {mp}{td}\rfloor\sum_{q\mid\frac dp,q\mid\frac tp}\mu(q)\\
=&\sum_d\mu(d)\lfloor\tfrac nd\rfloor\sum_{t\mid k}\sum_{r\mid d,r\mid t}\sum_{p\mid r}\mu(\tfrac rp)\lfloor\tfrac{mp}{td}\rfloor
\end{aligned}
\]

整理一下整除的关系：\(p\mid r\to r\mid t\to t\mid k\)，还有 \(r\mid d\)，简化一下式子，直接枚举 \((p,r,t)\)：

\[\begin{aligned}
&\sum_{p\mid r\mid t\mid k}\mu(\tfrac rp)\sum_{r\mid d}^{d\le n}\mu(d)\lfloor\tfrac nd\rfloor\lfloor\tfrac {mp}{td}\rfloor
\end{aligned}
\]

后边的那个求和可以写为

\[f(n,m,r)=\sum_{r\mid d}\mu(d)\lfloor\tfrac nd\rfloor\lfloor\tfrac md\rfloor
\]

继续推式子：

\[\begin{aligned}
f(n,m,r)&=\sum_{d=1}^{\lfloor n/r\rfloor}\mu(dr)\lfloor\tfrac n{dr}\rfloor\lfloor\tfrac m{dr}\rfloor\\
&=\sum_{d=1}^{\lfloor n/r\rfloor}\mu(d)\mu(r)\big[(r,d)=1\big]\lfloor\tfrac n{dr}\rfloor\lfloor\tfrac m{dr}\rfloor\\
&=\mu(r)\sum_{t=1}^{\lfloor n/r\rfloor}\mu(t)\sum_{t\mid d}^{\lfloor n/r\rfloor}\mu(d)\lfloor\tfrac n{dr}\rfloor\lfloor\tfrac m{dr}\rfloor\\
&=\mu(r)\sum_{t=1}^{\lfloor n/r\rfloor}\mu(t)f(\lfloor \tfrac nr\rfloor,\lfloor \tfrac mr\rfloor, t)
\end{aligned}
\]

当 \(r\neq1\) 时可以递归计算，只会递归 \(\mathcal O(\log n)\) 层，当 \(r=1\) 时

\[f(n,m,1)=\sum_{d=1}^n\mu(d)\lfloor\tfrac nd\rfloor\lfloor\tfrac md\rfloor
\]

可以数论分块+杜教筛。

还是下面这个做法比较小清新……

直接上正解吧，两个条件中取较简单的一个反演 —— \(k\) 是常数，所以尝试反演 \([(y,k)=1]\)：

\[\begin{aligned}
&\sum_{d\mid k}\mu(d)\sum_{d\mid y}^{y\le m}\sum_{x=1}^n\big[(x,y)=1\big]\\
=&\sum_{d\mid k}\mu(d)\sum_{y=1}^{\lfloor m/d\rfloor}\sum_{x=1}^{n}\big[(x,d)=1\big]\big[(x,y)=1\big]
\end{aligned}
\]

注意到后面的式子和原问题很像，实际上令 \(f(n,m,k)\)：

\[f(n,m,k)=\sum_{x=1}^n\sum_{y=1}^m\big[(x,y)=1\big]\big[(y,k)=1\big]
\]

则反演后的结果为：

\[f(n,m,k)=\sum_{d\mid k}\mu(d)f\Big(\big\lfloor\tfrac md\big\rfloor,n,d\Big)
\]

递归处理 \(d\gt1\) 的情况，直到 \(nm=0\) 答案为 \(0\)；对于 \(d=1\) 即 \(k=1\) 直接计算：

\[f(n,m,1)=\sum_{x=1}^n\sum_{y=1}^m[(x,y)=1]=\sum_{d}\lfloor\tfrac nd\rfloor\lfloor\tfrac md\rfloor\mu(d)
\]

直接数论分块+杜教筛。

---

# 小结

A 题有一定思维难度，不过题目给的部分分比较生艹，\(\mathcal O(n^2)\) 给到了 95pts，如果没有时间想正解拿了 95pts 也差不多了。

B 题纯粹考实现，也就是建图那部分。只要把答案只有 \(-1,0,1,2\) 这一点想到，正解就呼之欲出了，只是看实现问题，预估将会是考场上用时最长的一道题。

C 题的结论可以靠感知（背结论 awa）+暴力验证，我是写了一个 BSGS 来验证了 \(500\) 范围内是正确的，然后就默认结论没有错。不管怎么莫比乌斯反演，至少能够得到一个 \(\mathcal O(n\sigma_0(k))\) 的可以直接暴力算的式子，然后线性筛 \(\le2\times10^7\) 的就可以得到 84pts，应该是比较好的成绩了。说起来，要敢开数组，只要不爆空间，虽然看起来 \(\mathcal O(n\sigma_o(k))\) 跑 \(n=2\times10^7\) 看起来很离谱，但是敢写就能过……

---

# 源代码

差点忘了

几份代码写的时间间隔比较长，中途还改了码风……

点击展开/折叠 excellent.cpp

/*Lucky_Glass*/
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;

const int N = 30005;
#define con(typ) const typ &

int n, ncas;
int elg2[N], cnts[N], cntt[N];
char str[N];

struct Sa {
	int sa[N], rnk[N], nsa[N], nrnk[N], bin[N];
	int hgt[N][20];
	void clean(con(int) len) {
		memset(bin, 0, sizeof bin);
		for (int i = 1; i <= len; i++)
			rnk[i] = nrnk[i] = 0;
	}
	void build(char *sstr, con(int) len) {
		clean(len);
		for (int i = 1; i <= len; i++) bin[sstr[i] - 'a' + 1]++;
		for (int i = 1; i <= 26; i++) bin[i] += bin[i - 1];
		for (int i = 1; i <= len; i++) sa[bin[sstr[i] - 'a' + 1]--] = i;
		rnk[sa[1]] = 1;
		for (int i = 2; i <= len; i++) {
			rnk[sa[i]] = rnk[sa[i - 1]];
			if ( sstr[sa[i]] != sstr[sa[i - 1]]) rnk[sa[i]]++;
		}
		#define ikey(i) ((i) > len ? 0 : rnk[i])
		for (int l = 1; rnk[sa[len]] < len; l <<= 1) {
			for (int i = 1; i <= len; i++) bin[rnk[sa[i]]] = i;
			for (int i = len; i >= 1; i--)
				if ( sa[i] > l )
					nsa[bin[rnk[sa[i] - l]]--] = sa[i] - l;
			for (int i = len - l + 1; i <= len; i++)
				nsa[bin[rnk[i]]--] = i;
			nrnk[nsa[1]] = 1;
			for (int i = 2; i <= len; i++) {
				nrnk[nsa[i]] = nrnk[nsa[i - 1]];
				if ( ikey(nsa[i]) != ikey(nsa[i - 1])
					|| ikey(nsa[i] + l) != ikey(nsa[i - 1] + l) )
						nrnk[nsa[i]]++;
			}
			swap(rnk, nrnk), swap(sa, nsa);
		}
		for (int i = 1, j = 0; i <= len; i++) {
			if ( j ) j--;
			while ( rnk[i] < len && sstr[i + j] == sstr[sa[rnk[i] + 1] + j] ) j++;
			hgt[rnk[i]][0] = j;
		}
		// for (int i = 1; i < len; i++)
			// printf("%d%c", hgt[i][0], i == len - 1 ? '\n' : ' ');
		for (int i = len; i; i--)
			for (int j = 1; j < 20; j++)
				if ( i + (1 << (j - 1)) <= len )
					hgt[i][j] = min(hgt[i][j - 1], hgt[i + (1 << (j - 1))][j - 1]);
				else hgt[i][j] = hgt[i][j - 1];
	}
	int query(con(int) s, con(int) t) {
		if ( s > n || t > n ) exit(-1);
		int ss = rnk[s], tt = rnk[t];
		if ( ss > tt ) swap(ss, tt);
		tt--;
		int l = elg2[tt - ss + 1];
		return min(hgt[ss][l], hgt[tt - (1 << l) + 1][l]);
	}
} tol, tor;

void init() {
	elg2[1] = 0;
	for (int i = 2; i < N; i++)
		elg2[i] = elg2[i >> 1] + 1;
}
int matchR(con(int) s, con(int) t) {
	if ( s > n || t > n ) return 0;
	return tor.query(s, t);
}
int matchL(con(int) s, con(int) t) {
	return tol.query(n - s + 1, n - t + 1);
}
int main() {
	// freopen("input.in", "r", stdin);
	init();
	scanf("%d", &ncas);
	while ( ncas-- ) {
		scanf("%s", str + 1);
		n = (int) strlen(str + 1);
		for (int i = 1; i <= n; i++) cntt[i] = cnts[i] = 0;
		tor.build(str, n);
		reverse(str + 1, str + 1 + n);
		tol.build(str, n);
		for (int i = 1; i <= n; i++) {
			for (int j = i; j + i <= n; j += i) {
				int pl = matchL(j, j + i), pr = matchR(j + 1, j + i + 1);
				pl = min(pl, i), pr = min(pr, i - 1);
				int tmp = pr + pl - i + 1;
				if ( tmp > 0 ) {
					// printf("%d: start at [%d, %d]\n", i, i - pl + 1, i - pl + tmp);
					// printf("%d: end at [%d, %d]\n", i, i - pl + 2 * i, i - pl - 1 + tmp + 2 * i);
					cnts[j - pl + 1]++, cnts[j - pl + 1 + tmp]--;
					cntt[j - pl + 2 * i]++, cntt[j - pl + tmp + 2 * i]--;
				}
			}
		}
		for (int i = 1; i <= n; i++) cnts[i] += cnts[i - 1], cntt[i] += cntt[i - 1];
//		for (int i = 1; i <= n; i++)
//			printf("start at %d = %d\n", i, cnts[i]);
		long long ans = 0;
		for (int i = 1; i < n; i++)
			ans += 1ll * cnts[i + 1] * cntt[i];
		printf("%lld\n", ans);
	}
	return 0;
}

点击展开/折叠 grid.cpp

/*Lucky_Glass*/
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;

const int DIR[9][2] = {
  {-1, -1}, {-1, 0}, {-1, 1},
  {0, -1}, {0, 0}, {0, 1},
  {1, -1}, {1, 0}, {1, 1}
};

inline int rin(int &r) {
  int b = 1, c = getchar(); r = 0;
  while ( c < '0' || '9' < c ) b = c == '-' ? -1 : b, c = getchar();
  while ( '0' <= c && c <= '9' ) r = (r * 10) + (c ^ '0'), c = getchar();
  return r *= b;
}

const int N = 1e5 + 10, NP = N * 20, NE = N * 80;
#define con(typ) const typ &

struct Graph {
  int head[NP], to[NE], nxt[NE], ncnt, np;
  void addEdge(con(int) u, con(int) v) {
    int p = ++ncnt, q = ++ncnt;
    to[p] = v, nxt[p] = head[u], head[u] = p;
    to[q] = u, nxt[q] = head[v], head[v] = q;
  }
  inline int operator [] (con(int) u) const {return head[u];}
} gr;

struct SPNode {
  int x, y, tag;
  bool operator < (con(SPNode) p) const {
    if ( x == p.x ) return y < p.y;
    return x < p.x;
  }
} nod[N * 9];

bool isans1;
int ncas, n, m, nc, nnod, itmp, ndfn;
int dfn[NP], low[NP];
bool ptag[NP];
int tmp[2][NP][3], ntmp[2];
pair<int, int> pos[N];

void dfs(con(int) u) {
  bool iscut = false;
  int cntson = 0;
  dfn[u] = low[u] = ++ndfn;
  for (int it = gr[u]; it; it = gr.nxt[it]) {
    int v = gr.to[it];
    if ( dfn[v] ) low[u] = min(low[u], dfn[v]);
    else {
      cntson++;
      dfs(v);
      low[u] = min(low[u], low[v]);
      if ( low[v] >= dfn[u] )
        if ( ptag[u] )
          iscut = true;
    }
  }
  if ( iscut )
    isans1 |= (u != 1 || cntson > 1);
}
void newTemp() {itmp ^= 1, ntmp[itmp] = 0;}
void setTemp(con(int) l, con(int) r, con(bool) tag) {
  int p = ++gr.np;
  if ( p >= NP ) exit(0);
  dfn[p] = 0, gr.head[p] = 0;
  ptag[p] = tag;
  tmp[itmp][++ntmp[itmp]][0] = l, tmp[itmp][ntmp[itmp]][1] = r;
  tmp[itmp][ntmp[itmp]][2] = p;
}
void arrangeTemp() {
  for (int i = 1; i < ntmp[itmp]; i++)
    if ( tmp[itmp][i][1] + 1 == tmp[itmp][i + 1][0] )
      gr.addEdge(tmp[itmp][i][2], tmp[itmp][i + 1][2]);
  if ( !ntmp[0] || !ntmp[1] ) return;
  for (int i = 1, jl = 1, jr = 0; i <= ntmp[0]; i++) {
    while ( jr < ntmp[1] && tmp[1][jr + 1][0] <= tmp[0][i][1] ) jr++;
    while ( jl <= jr && tmp[1][jl][1] < tmp[0][i][0] ) jl++;
    for (int j = jl; j <= jr; j++)
      gr.addEdge(tmp[0][i][2], tmp[1][j][2]);
  }
}

bool bf[N];

bool isNeg() {
  if ( 1ll * n * m - nc > 2 ) return false;
  if ( 1ll * n * m - nc <= 1 ) return true;
  #define id(x, y) ((x) * m - m + (y))
  for (int i = 1; i <= n; i++)
    for (int j = 1; j <= m; j++)
      bf[id(i, j)] = false;
  for (int i = 1; i <= nc; i++)
    bf[id(pos[i].first, pos[i].second)] = true;
  const int DIR[4][2] = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
  for (int i = 1; i <= n; i++) for (int j = 1; j <= m; j++)
    if ( !bf[id(i, j)] )
      for (int k = 0; k < 4; k++) {
        int x = i + DIR[k][0], y = j + DIR[k][1];
        if ( 1 <= x && x <= n && 1 <= y && y <= m && !bf[id(x, y)] )
          return true;
      }
  return false;
  #undef id
}
int main() {
  rin(ncas);
  while ( ncas-- ) {
    ndfn = nnod = 0;
    gr.np = gr.ncnt = 0;
    itmp = 0;
    isans1 = false;
    //
    rin(n), rin(m), rin(nc);
    for (int i = 1; i <= nc; i++)
      rin(pos[i].first), rin(pos[i].second);
    if ( isNeg() ) {printf("-1\n"); continue;}
    sort(pos + 1, pos + 1 + nc);
    if ( m == 1 ) {
      int cnti = 0;
      if ( nc ) {
        if ( pos[1].first > 1 ) cnti++;
        for (int i = 2; i <= nc; i++)
          if ( pos[i - 1].first + 1 <= pos[i].first - 1 )
            cnti++;
        if ( pos[nc].first < n ) cnti++;
      } else cnti = 1;
      if ( cnti > 1 ) printf("0\n");
      else printf("1\n");
      continue;
    }
    if ( n == 1 ) {
      int cnti = 0;
      if ( nc ) {
        if ( pos[1].second > 1 ) cnti++;
        for (int i = 2; i <= nc; i++)
          if ( pos[i - 1].second + 1 <= pos[i].second - 1 )
            cnti++;
        if ( pos[nc].second < m ) cnti++;
      } else cnti = 1;
      if ( cnti > 1 ) printf("0\n");
      else printf("1\n");
      continue;
    }
    for (int i = 1, p, q; i <= nc; i++) {
      p = pos[i].first, q = pos[i].second;
      for (int k = 0; k < 9; k++) {
        int x = p + DIR[k][0], y = q + DIR[k][1];
        if ( 1 <= x && x <= n && 1 <= y && y <= m ) {
          // cerr << "build " << x << ' ' << y << endl;
          nod[++nnod].x = x, nod[nnod].y = y, nod[nnod].tag = k == 4;
        }
      }
    }
    //
    sort(nod + 1, nod + 1 + nnod);
    ntmp[0] = ntmp[1] = 0;
    if ( nod[1].x > 1 ) newTemp(), setTemp(1, m, false);
    int lasl = nod[1].x - 1;
    for (int i = 1; i <= nnod; i++) {
      if ( lasl < nod[i].x - 1 ) {
        newTemp(), setTemp(1, m, false);
        arrangeTemp();
      }
      newTemp();
      if ( nod[i].y > 1 ) setTemp(1, nod[i].y - 1, false);
      int toi = i; while ( toi < nnod && nod[toi + 1].x == nod[i].x ) toi++;
      for (int j = i; j <= toi; j++) {
        int toj = j; bool itag = nod[j].tag;
        while ( toj < toi && nod[toj + 1].y == nod[j].y )
          itag |= nod[++toj].tag;
        if ( !itag) setTemp(nod[j].y, nod[j].y, true);
        if ( toj < toi && nod[j].y + 1 < nod[toj + 1].y )
          setTemp(nod[j].y + 1, nod[toj + 1].y - 1, false);
        j = toj;
      }
      if ( nod[toi].y < m ) setTemp(nod[toi].y + 1, m, false);
      arrangeTemp();
      lasl = nod[i].x, i = toi;
    }
    if ( lasl < n ) {
      newTemp(), setTemp(1, m, false);
      arrangeTemp();
    }
    dfs(1);
    if ( ndfn < gr.np ) printf("0\n");
    else if ( isans1 ) printf("1\n");
    else printf("2\n");
  }
  return 0;
}

点击展开/折叠 cyclic.cpp

/*Lucky_Glass*/
#include <cstdio>
#include <cstring>
#include <algorithm>

typedef long long llong;
#define con(typ) const typ &
const int M = 1e6 + 10, HMOD = 1000793;

int dv[200], prm[M], mu[M], summu[M];
bool bok[M];
int ndv, nprm;

struct HashTable {
  int head[HMOD], nxt[M << 1], val[M << 1], key[M << 1];
  int ncnt;
  int& operator [] (con(int) _key) {
    for (int it = head[_key % HMOD]; it; it = nxt[it])
      if ( key[it] == _key )
        return val[it];
    int p = ++ncnt;
    key[p] = _key, nxt[p] = head[_key % HMOD], head[_key % HMOD] = p;
    return val[p] = 2e9;
  }
} htab;

void init(con(int) vk) {
  mu[1] = 1;
  for (int i = 2; i < M; ++i) {
    if ( !bok[i] ) mu[i] = -1, prm[++nprm] = i;
    for (int j = 1; j <= nprm && 1ll * prm[j] * i < M; ++j) {
      bok[i * prm[j]] = true;
      if ( i % prm[j] == 0 ) break;
      mu[i * prm[j]] = -mu[i];
    }
  }
  for (int i = 1; i < M; ++i) summu[i] = summu[i - 1] + mu[i];
  for (int i = 1; i <= vk; ++i)
    if ( vk % i == 0 && mu[i] )
      dv[++ndv] = i;
}
int funSum(con(int) n) {
  if ( n < M ) return summu[n];
  int &ret = htab[n];
  if ( ret != 2e9 ) return ret;
  llong tmp = 1;
  for (int i = 2; i <= n; ++i) {
    int ii = n / (n / i);
    tmp -= (ii - i + 1ll)  * funSum(n / i);
    i = ii;
  }
  return ret = (int)tmp;
}
llong fun(con(int) n, con(int) m, con(int) vk) {
  if ( !n || !m ) return 0ll;
  llong ret = 0;
  if ( vk == 1 ) {
    int las = 0;
    for (int i = 1, li = std::min(n, m); i <= li; ++i) {
      int ii = std::min(n / (n / i), m / (m / i)), tmp = funSum(ii);
      ret += 1ll * (n / i) * (m / i) * (tmp - las);
      las = tmp;
      i = ii;
    }
    return ret;
  }
  if ( vk < ndv ) {
    for (int i = 1; i <= vk; ++i)
      if ( vk % i == 0 && mu[i] )
        ret += mu[i] * fun(m / i, n, i);
  } else {
    for (int i = 1; i <= ndv; ++i)
      if ( vk % dv[i] == 0 )
        ret += mu[dv[i]] * fun(m / dv[i], n, dv[i]);
  }
  return ret;
}
int main() {
  int n, m, vk;
  scanf("%d%d%d", &n, &m, &vk);
  init(vk);
  printf("%lld\n", fun(n, m, vk));
  return 0;
}

---

THE END

Thanks for reading!

准备升空 到广阔云漠中

日出穿透我安睡的眼眸

整个世界 所有声音在视线上跳动

尽情弹奏属于我的与众不同

——《世界不静默》 By 双笙

> Link 世界不静默 - Bilibili