5.31 NOI 模拟
\(T1\ Beauty\)



\(T2\ Jump\)
考场上一开始想的是树套树,然后我看到了\(128MB,\)好
于是乎附上\(56pts\ MLE\)代码在空间\(512MB\)可以获得\(84pts,\)时限调到\(8s,\)可以\(AC\)
#define Eternal_Battle ZXK
#include<bits/stdc++.h>
#define MAXN 200005
using namespace std;
struct City
{
int x,y;
}cy[MAXN];
struct Link
{
int val,l,r,u,d;
};
vector<Link>rd[MAXN];
int dis[MAXN],ID1,ID2,rt,n,m,h,w;
bool vis[MAXN];
struct Tr1
{
int l,r,ls,rs;
int rt;
}tr1[MAXN<<3];
struct node
{
int l,r,ls,rs;
vector<int>Get;
}tr2[MAXN<<3];
priority_queue<pair<int,int>,vector<pair<int,int> >,greater<pair<int,int> > >q;
void Query2(int now,int L,int R,int l,int r,int st,int val)
{
if(!now) return ;
if(L>=l&&R<=r)
{
for(int i=0;i<tr2[now].Get.size();i++)
{
int y=tr2[now].Get[i];
if(dis[y]>dis[st]+val)
{
dis[y]=dis[st]+val;
q.push(make_pair(dis[y],y));
}
}
return ;
}
int mid=(L+R)>>1;
if(l<=mid) Query2(tr2[now].ls,L,mid,l,r,st,val);
if(r>mid) Query2(tr2[now].rs,mid+1,R,l,r,st,val);
}
void Query1(int now,int L,int R,int l,int r,int u,int d,int st,int val)
{
if(!now) return ;
// cout<<"Ins1: "<<st<<" "<<L<<" "<<R<<"\n";
if(L>=l&&R<=r)
{
Query2(tr1[now].rt,1,w,u,d,st,val);
return ;
}
int mid=(L+R)>>1;
if(l<=mid) Query1(tr1[now].ls,L,mid,l,r,u,d,st,val);
if(r>mid) Query1(tr1[now].rs,mid+1,R,l,r,u,d,st,val);
}
void dij()
{
memset(dis,0x3f,sizeof(dis));
q.push(make_pair(dis[1],1));
dis[1]=0;
while(q.size())
{
int now=q.top().second;
q.pop();
if(vis[now]) continue;
vis[now]=true;
for(int i=0;i<rd[now].size();i++)
{
int val=rd[now][i].val;
int l=rd[now][i].l;
int r=rd[now][i].r;
int u=rd[now][i].u;
int d=rd[now][i].d;
Query1(rt,1,h,l,r,u,d,now,val);
continue;
for(int j=1;j<=n;j++)
{
if(cy[j].x>=l&&cy[j].x<=r&&cy[j].y>=u&&cy[j].y<=d)
{
if(dis[j]>dis[now]+val)
{
dis[j]=dis[now]+val;
q.push(make_pair(dis[j],j));
continue;
}
}
}
}
}
}
void Insert2(int &now,int l,int r,int y,int id)
{
if(l>y||r<y) return ;
if(!now) now=++ID2;
// cout<<"Ins2: "<<now<<" "<<l<<" "<<r<<" "<<y<<" "<<id<<"\n";
tr2[now].Get.push_back(id);
if(l==r) return ;
int mid=(l+r)>>1;
Insert2(tr2[now].ls,l,mid,y,id);
Insert2(tr2[now].rs,mid+1,r,y,id);
}
void Insert1(int &now,int l,int r,int x,int y,int id)
{
if(l>x||r<x) return ;
if(!now) now=++ID1;
// cout<<"Ins1: "<<l<<" "<<r<<" "<<x<<"\n";
Insert2(tr1[now].rt,1,w,y,id);
if(l==r) return ;
int mid=(l+r)>>1;
Insert1(tr1[now].ls,l,mid,x,y,id);
Insert1(tr1[now].rs,mid+1,r,x,y,id);
}
int main()
{
freopen("jump.in","r",stdin);
freopen("jump.out","w",stdout);
scanf("%d%d%d%d",&n,&m,&h,&w);
for(int i=1;i<=n;i++)
{
scanf("%d%d",&cy[i].x,&cy[i].y);
Insert1(rt,1,h,cy[i].x,cy[i].y,i);
}
for(int i=1,l,r,u,d,cs,poz;i<=m;i++)
{
scanf("%d%d%d%d%d%d",&poz,&cs,&l,&r,&u,&d);
rd[poz].push_back((Link){cs,l,r,u,d});
}
dij();
for(int i=2;i<=n;i++)
{
printf("%d\n",dis[i]);
}
}
我把内层线段树用\(set\)代替,好,只有\(60pts\)是怎么会是呢?
附上\(60pts\ TLE\)代码,常数真的很大
#define Eternal_Battle ZXK
#include<bits/stdc++.h>
#define MAXN 260005
using namespace std;
template<class T>
T Read()
{
T x=0,f=1;
char ch=getchar();
while(ch<'0'||ch>'9')
{
if(ch=='-')
f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9')
{
x=(x<<1)+(x<<3)+(ch^'0');
ch=getchar();
}
return x*f;
}
int (*read)()=Read<int>;
#define read Read<int>
struct Link
{
int val,l,r,u,d;
};
vector<Link>rd[MAXN];
int dis[MAXN],ID1,ID2,rt,n,m,h,w;
bool vis[MAXN];
struct Tr1
{
int ls,rs;
set<pair<int,int> >Get;
}tr1[MAXN<<2];
priority_queue<pair<int,int>,vector<pair<int,int> >,greater<pair<int,int> > >q;
void Query1(int now,int L,int R,int l,int r,int u,int d,int st,int val)
{
if(!now) return ;
// cout<<"Ins1: "<<st<<" "<<L<<" "<<R<<"\n";
if(L>=l&&R<=r)
{
pair<int,int>Now;
Now=make_pair(u,0);
set<pair<int,int> >::iterator it=tr1[now].Get.lower_bound(Now);
for(;it->first<=d&&it!=tr1[now].Get.end();it++)
{
int y=it->second;
if(dis[y]>dis[st]+val)
{
dis[y]=dis[st]+val;
q.push(make_pair(dis[y],y));
}
}
return ;
}
int mid=(L+R)>>1;
if(l<=mid) Query1(tr1[now].ls,L,mid,l,r,u,d,st,val);
if(r>mid) Query1(tr1[now].rs,mid+1,R,l,r,u,d,st,val);
}
void dij()
{
memset(dis,0x3f,sizeof(dis));
q.push(make_pair(dis[1],1));
dis[1]=0;
while(q.size())
{
int now=q.top().second;
q.pop();
if(vis[now]) continue;
vis[now]=true;
for(int i=0;i<rd[now].size();i++)
{
int val=rd[now][i].val;
int l=rd[now][i].l;
int r=rd[now][i].r;
int u=rd[now][i].u;
int d=rd[now][i].d;
Query1(rt,1,h,l,r,u,d,now,val);
}
}
}
void Insert1(int &now,int l,int r,int x,int y,int id)
{
if(l>x||r<x) return ;
if(!now) now=++ID1;
tr1[now].Get.insert(make_pair(y,id));
if(l==r) return ;
int mid=(l+r)>>1;
Insert1(tr1[now].ls,l,mid,x,y,id);
Insert1(tr1[now].rs,mid+1,r,x,y,id);
}
int main()
{
freopen("jump.in","r",stdin);
freopen("jump.out","w",stdout);
scanf("%d%d%d%d",&n,&m,&h,&w);
for(int i=1,x,y;i<=n;i++)
{
x=read(); y=read();
Insert1(rt,1,h,x,y,i);
}
for(int i=1,l,r,u,d,cs,poz;i<=m;i++)
{
poz=read(); cs=read(); l=read(); r=read(); u=read(); d=read();
rd[poz].push_back((Link){cs,l,r,u,d});
}
dij();
for(int i=2;i<=n;i++)
{
printf("%d\n",dis[i]);
}
}
加上一些优化,得到外层线段树套\(set\)代码,怎么这个技巧这么\(Nb\)呢?
附上\(100pts\)代码
#define Eternal_Battle ZXK
#include<bits/stdc++.h>
#define MAXN 150005
using namespace std;
int rd()
{
int f=1,ans=0;char c=getchar();
while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
while(c>='0'&&c<='9'){ans=ans*10+c-'0';c=getchar();}
return f*ans;
}
priority_queue<pair<int,int> > que;
set<pair<int,int> >s[MAXN<<2];
int dis[MAXN<<2],vis[MAXN<<2],head[MAXN],cnt;
struct spe
{
int x,y;
}g[MAXN];
struct Segment
{
#define ls (k<<1)
#define rs ((k<<1)|1)
void change(int k,int l,int r,int x,int y,int id)
{
s[k].insert(make_pair(g[id].y,id));
if(l==r) return;
int mid=(l+r)>>1;
if(x<=mid) change(ls,l,mid,x,y,id);
if(mid<y) change(rs,mid+1,r,x,y,id);
return;
}
void Query(int k,int l,int r,int x,int y,int L,int R,int id)
{
if(x<=l&&r<=y)
{
set<pair<int,int> >:: iterator it;
while(!s[k].empty())
{
it=s[k].lower_bound(make_pair(L,-1));
if(it==s[k].end()||(*it).first>R) break;
int v=(*it).second;
if(dis[v]>dis[id])
{
dis[v]=dis[id];
que.push(make_pair(-dis[v],v));
}
s[k].erase(*it);
}
return;
}
int mid=(l+r)>>1;
if(x<=mid) Query(ls,l,mid,x,y,L,R,id);
if(mid<y) Query(rs,mid+1,r,x,y,L,R,id);
return;
}
}tr;
int n,m,w,h;
struct node
{
int u,v,nex;
}x[MAXN<<1];
struct Spe
{
int be,w,l,r,d,u;
}f[MAXN];
void add(int u,int v)
{
x[cnt].u=u,x[cnt].v=v,x[cnt].nex=head[u],head[u]=cnt++;
}
int main()
{
freopen("jump.in","r",stdin);
freopen("jump.out","w",stdout);
memset(head,-1,sizeof(head));
n=rd(),m=rd(),w=rd(),h=rd();
for(int i=1;i<=n;i++)
{
g[i].x=rd(),g[i].y=rd();
tr.change(1,1,w,g[i].x,g[i].x,i);
}
for(int i=1;i<=m;i++)
{
f[i].be=rd(),f[i].w=rd();
f[i].l=rd(),f[i].r=rd();
f[i].d=rd(),f[i].u=rd();
add(f[i].be,i);
}
memset(dis,0x3f,sizeof(dis));
dis[1]=0;que.push(make_pair(0,1));
while(!que.empty())
{
int xx=que.top().second;que.pop();
if(vis[xx]) continue;
vis[xx]=1;
if(xx>n)
{
tr.Query(1,1,w,f[xx-n].l,f[xx-n].r,f[xx-n].d,f[xx-n].u,xx);
continue;
}
for(int i=head[xx];i!=-1;i=x[i].nex)
{
int v=x[i].v+n;
if(dis[v]>dis[xx]+f[x[i].v].w)
{
dis[v]=dis[xx]+f[x[i].v].w;
que.push(make_pair(-dis[v],v));
}
}
}
for(int i=2;i<=n;i++) printf("%d\n",dis[i]);
return 0;
}
\(T3\ Combination\)
\\
=\sum_{0\le i\le n}[k|i]\binom{n}{i}
\]
单位根反演
\]
反代
\\
=\frac{1}{k}\sum_{j=0}^{k-1}\sum_{0\le i\le n}(w_k^j)^i\binom{n}{i}
\]
较为显然的二项式形式
\]
在\(\mod=998244353\)可以直接计算
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define maxn 100010
const int p=998244353;
int n,k;
int ksm(int a,int b)
{
int ans=1;
for(;b;b>>=1,a=a*a%p)
if(b&1)ans=ans*a%p;
return ans;
}
int w,wn=1;
int ans;
signed main()
{
cin>>n>>k;
w=ksm(114514,(p-1)/k);
for(int i=0;i<k;i++,wn=wn*w%p)
ans=(ans+ksm(1+wn,n%(p-1)))%p;
ans=ans*ksm(k,p-2)%p;
cout<<ans;
}
我发现我的\(NTT\)真的只是背过的,我连模数意义下的单位根都不熟练
\(w_k=3^{(mod -1)/k}\)
至于\(\mod=998244853\)
可以使用多项式快速幂计算,复杂度\(O(k\log(n)\log(k))\)
然后发现题干中有一句话\(k=2^p\)
设\(const(F(x))=[x^0]F(x)\)
打表发现
\(const((1+w_k^i)^n)=const((1+w_k)^n)\)
证明略
然后下面的式子就很通俗易懂了
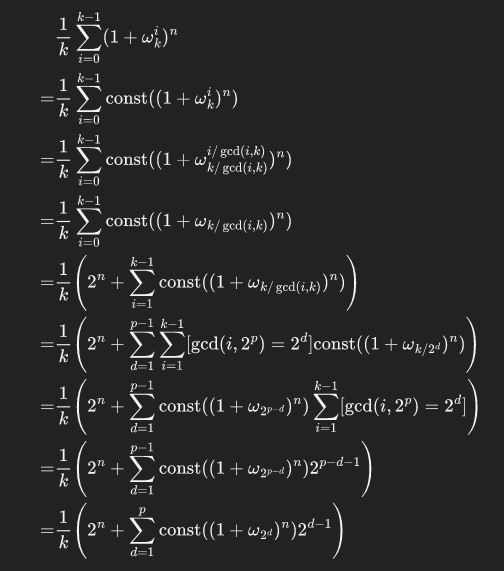
而且发现了一个很nb的操作,在mod 998244353时,原根可以写114514!!!
于是乎我们的\(NTT\)可以这么写
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int G=114514,mod=998244353;
原根性质,\(a^{\phi(m)}=1(\mod m)\)
\(k\)次单位根\(a^{(mod-1)/k}\)
然后代码
#include<bits/stdc++.h>
#define mo 998244853
#define base 35000
using namespace std;
const double Pie=acos(-1);
inline long long readl()
{
long long r(0);char in=getchar();while(in<'0'||in>'9')in=getchar();
while(in>='0'&&in<='9')r=(r<<1)+(r<<3)+(in^48),in=getchar();return r;
}
inline int read()
{
int r(0);char in=getchar();while(in<'0'||in>'9')in=getchar();
while(in>='0'&&in<='9')r=(r<<1)+(r<<3)+(in^48),in=getchar();return r;
}
inline int MO(int x){return x<mo?x:x-mo;}
inline int poww(int x,int y)
{
int r(1);
while(y)
{
if(y&1)r=1ll*r*x%mo;
x=1ll*x*x%mo;
y>>=1;
}
return r;
}
struct num:public pair<double,double>
{
num(int x):pair<double,double>(x/base,x%base){}
num(double x,double y):pair<double,double>(x,y){}
int tnt(){return (int)round(first*base+second);}
friend num operator ~(const num &x){return num(x.first,-x.second);}
friend num operator /(const num &x,const double &y){return num(x.first/y,x.second/y);}
friend num operator +(const num &x,const num &y){return num(x.first+y.first,x.second+y.second);}
friend num operator -(const num &x,const num &y){return num(x.first-y.first,x.second-y.second);}
friend num operator *(const num &x,const num &y){return num(x.first*y.first-x.second*y.second,x.first*y.second+x.second*y.first);}
friend pair<num,num> gt(const num &a0,const num &a1,const num &b0,const num &b1)
{
num x0=(a0+a1)/2,x1=(a1-a0)/2*num(0,1),y0=(b0+b1)/2,y1=(b1-b0)/2*num(0,1);
return pair<num,num>(x0*y0+x1*y1*num(0,1),x0*y1+x1*y0*num(0,1));
}
friend num gt(const num &x,const num &y)
{
int nw=MO(1ll*MO((1ll*MO((long long)round(x.first)%mo+mo)*base%mo)+MO((long long)round(y.first+y.second)%mo+mo))*base%mo+MO((long long)round(x.second)%mo+mo));return num(nw/base,nw%base);
}
};
struct Poly:public vector<num>
{
int len;static vector<int>pos;
Poly(){}
Poly(const vector<num>&x){assign(x.begin(),x.end());len=x.size()-1;}
void dft(int len)
{
resize(len,num(0,0));for(int i=0;i<len;i++)if(pos[i]<i)std::swap(at(pos[i]),at(i));
for(int i=2;i<=len;i<<=1)
{
int leng=i>>1;
for(int j=0;j<len;j+=i)for(int k=0;k<leng;k++)
{
num nw=num(cos(Pie*k/leng),sin(Pie*k/leng))*at(j+k+leng);
at(j+k+leng)=at(j+k)-nw;at(j+k)=at(j+k)+nw;
}
}
}
void idft(int len)
{
for(int i=0;i<len;i++)if(pos[i]<i)std::swap(at(pos[i]),at(i));
for(int i=2;i<=len;i<<=1)
{
int leng=i>>1;
for(int j=0;j<len;j+=i)for(int k=0;k<leng;k++)
{
num nw=num(cos(Pie*k/leng),-sin(Pie*k/leng))*at(j+k+leng);
at(j+k+leng)=at(j+k)-nw;at(j+k)=at(j+k)+nw;
}
}
for(int i=0;i<len;i++)at(i)=at(i)/len;
}
friend Poly operator *(Poly x,Poly y)
{
int leng=x.len,len=leng+1;pos.assign(len,0);
for(int i=0;i<len;i++)pos[i]=(pos[i>>1]>>1)|(i&1?len>>1:0);x.dft(len),y.dft(len);
Poly p,q;p.assign(len,num(0,0));q.assign(len,num(0,0));
tie(p.front(),q.front())=gt(x.front(),~x.front(),y.front(),~y.front());
for(int i=1;i<len;i++)tie(p[i],q[i])=gt(x[i],~x[len-i],y[i],~y[len-i]);
x.assign(leng+1,num(0,0));y.clear();x.len=leng;p.idft(len);q.idft(len);
for(int i=0;i<=leng;i++)x[i]=gt(p[i],q[i]);return x;
}
friend Poly operator %(Poly x,int y)
{
if(y<x.len)x.len=y,x.resize(y+1,num(0,0));return x;
}
friend Poly gtnv(Poly z)
{
vector<int>seq;int le=z.len+1;while(le>1)seq.push_back(le-1),le=(le+1)>>1;reverse(seq.begin(),seq.end());Poly y(vector<num>(1,num(poww(z[0].tnt(),mo-2))));
for(vector<int>::iterator ite=seq.begin();ite!=seq.end();ite++)
{
Poly x=z%*ite;x=x*y%*ite;x.front()=num(MO(mo+2-x.front().tnt()));for(iterator ite=x.begin()+1;ite!=x.end();ite++)*ite=num(MO(mo-ite->tnt()));y=y*x%*ite;
}
return y;
}
};
vector<int>Poly::pos;
long long n;
int m;
int main()
{
n=readl();
m=read();
Poly f,g;
f.assign(m,num(0));
g.assign(m,num(0));
f.len=g.len=m-1;
f[0]=g[0]=num(1);
f[1%m]=f[1%m]+1;
while(n)
{
if(n&1)g=g*f;
f=f*f;
n>>=1;
}
printf("%d",g[0].tnt());
return 0;
}
5.31 NOI 模拟的更多相关文章
- 5.23 NOI 模拟
$5.23\ NOI $模拟 \(T1\)简单的计算几何题 \(zjr:\)我当时没改,那么自己看题解吧 倒是有个简单的随机化方法(能获得\(72pts,\)正确性未知)\(:\) 随机两条切椭圆的平 ...
- 5.30 NOI 模拟
$5.30\ NOI $模拟 高三大哥最后一次模拟考了,祝他们好运 \(T1\)装箱游戏 显然可以将四种字母之间的空缺当做状态枚举 那么这道题就很显然了 #include<bits/stdc++ ...
- 5.6 NOI模拟
\(5.6\ NOI\)模拟 明天就母亲节了,给家里打了个电话(\(lj\ hsez\)断我电话的电,在宿舍打不了,只能用教练手机打了) 其实我不是很能看到自己的\(future,\)甚至看不到高三的 ...
- 5.4 NOI模拟
\(5.4\ NOI\)模拟 \(T1\) 想到分讨,但是暴力输出一下方案之后有很多特别的情况要讨论,就弃了... 假设\(a\)是原序列,\(b\)是我们得到的序列 设\(i\)是最长公共前缀,\( ...
- NOI模拟赛 Day1
[考完试不想说话系列] 他们都会做呢QAQ 我毛线也不会呢QAQ 悲伤ING 考试问题: 1.感觉不是很清醒,有点困╯﹏╰ 2.为啥总不按照计划来!!! 3.脑洞在哪里 4.把模拟赛当作真正的比赛,紧 ...
- NOI 模拟赛 #2
得分非常惨惨,半个小时写的纯暴力 70 分竟然拿了 rank 1... 如果 OYJason 和 wxjor 在可能会被爆踩吧 嘤 T1 欧拉子图 给一个无向图,如果一个边集的导出子图是一个欧拉回路, ...
- 【2018.12.10】NOI模拟赛3
题目 WZJ题解 大概就是全场就我写不过 $FFT$ 系列吧……自闭 T1 奶一口,下次再写不出这种 $NTT$ 裸题题目我就艹了自己 -_-||| 而且这跟我口胡的自创模拟题 $set1$ 的 $T ...
- 6.28 NOI模拟赛 好题 状压dp 随机化
算是一道比较新颖的题目 尽管好像是两年前的省选模拟赛题目.. 对于20%的分数 可以进行爆搜,对于另外20%的数据 因为k很小所以考虑上状压dp. 观察最后答案是一个连通块 从而可以发现这个连通块必然 ...
- 6.17 NOI 模拟
\(T1\ crime\) 计算几何\(+\)最短路,我的写法很麻烦 比较无脑,直接扫一遍判断能否连接即可,需要特别判断对角线的情况 #include<bits/stdc++.h> #de ...
随机推荐
- 在Windows2003 server 64位系统上使用ArcEngine开发的WCF服务
之前大篇文章提到,ESRI说AE10.0以后已经不支持WebService的发布,经过一段时间的测试,发现目前10.2.2版本开始的WCF服务都可以正常发布,且运行正常. 先说一下之前遇到的问题,本机 ...
- CSS基础学习(二)
11.CSS背景 ①设置背景颜色(颜色值通常可以用十六进制(如#000000)或者颜色名称(如red)来表示) 属性:background-color 例: body { background-col ...
- Vue2-组件通讯传值
Vue2组件通讯传值 方法 Slot插槽--父向子内容分发,子组件只读 mixin混入--定义公共变量或方法,mixin数据不共享,组件中mixin实例互不影响 provide+inject--依赖注 ...
- LSP原则是什么
如果这篇文章能够帮到您,请给我一个免费的赞,谢谢QWQ! LSP原则并不难,但是地方就会把它说的很啰嗦,如果你对LSP还是感到疑惑,请往下看看. 先上代码: public class Bird { p ...
- ElasticSearch6.4.2
做一个简单的API记录 1.依赖为6.4.2 比较老的版本 2.指定ES集群,可接多个Put(); Setting setting=Setting.builder().put("clust ...
- Mysql中文存储、显示及不区分大小写控制
刚开始使用mysql,以为安装了完了就可以使用了,结果是我太天真了.mysql5.7版本,默认严格区分大小写,并且不支持中文存储. 严格区分大小写,即A表和a表示两个不同的表 实例 修改 在/etc/ ...
- php 图片转换二进制数
$image = "1.jpg"; //图片地址 $fp = fopen($image, 'rb'); $content = fread($fp, filesize($image) ...
- TypeScript 泛型(generic) 入门介绍
TypeScript 泛型函数 下面来创建第一个使用泛型的例子:identity函数.这个函数会返回任何传入它的值.你可以把这个函数当成是echo命令.不用泛型的话,这个函数可能是下面这样: func ...
- SAP APO - Architecture
SAP APO体系结构由多个组件组成-数据库,BI环境包含InfoCube和实时缓存. InfoCube是BI数据集市的一部分,实时缓存是您保留与计划和调度有关的所有数据的主要区域. 您可以在实时缓存 ...
- 论文解读(LG2AR)《Learning Graph Augmentations to Learn Graph Representations》
论文信息 论文标题:Learning Graph Augmentations to Learn Graph Representations论文作者:Kaveh Hassani, Amir Hosein ...
