Python之枚举法解数学题

作为初二的学生，数学题总是令我苦恼的问题。尤其是我们这里的预备班考试（即我们这里最好的两所高中提前一年招生，选拔尖子生的考试）将近，我所面对的数学题越发令人头疼。

这不，麻烦来了：

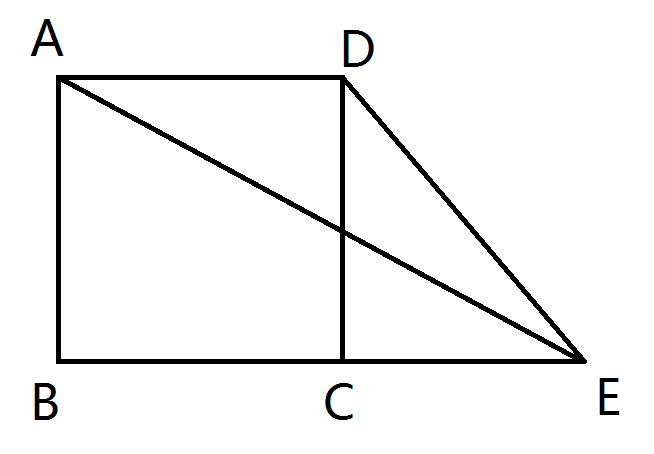
如图,在正方形ABCD中，E在射线BC上，连接AE、CE，则DE/AE的最小值为________.

拿到这题，信心慢慢的我从容淡定地设AB:CE为1:x，即AB=k，CE=xk，于是原式（设为y）=[k^2+(xk)^2]^0.5/[k^2+(k+xk)^2]^0.5（这里的“^”代表乘方）。这不就只要求[k^2+(xk)^2]/[k^2+(k+xk)^2]的最小值嘛！这是一个求代数式最小值的问题。

可是……越看越不对劲。这个代数式是个分式，而我们常接触的同类型题涉及的都只是整式。凭着我对六本初中数学书的印象，我不禁提出疑问：这真的是初中的内容吗？书上似乎只字未提吧？

但是，本着埋头苦干的老黄牛精神，我就在那里毫无结果地和这道题目耗了几个小时。最终，我放弃了。

但也许是梦里来的灵感，第二天早上，我突然想到：何不通过一个Python程序来逐个列举，从中选择近似值呢？

于是，第一个程序出来了：

k=1
answer=100
myx=0
for x in range(10):
    y=(k**2+(x*k)**2)**0.5/(k**2+(k+x*k)**2)**0.5
    if y<answer:
        answer=y
        myx=x
print(answer,myx)

输出结果：

0.6324555320336759 1

唉，怎么越看越不对劲？

最后，我终于发现问题的所在：像这样遍历x，它的值都是整数，而事实上最小的y所对应的x不一定是整数。

那好，我们改：

k=1
answer=100
myx=0
for x in range(10000):
    x=x/1000
    y=(k**2+(x*k)**2)**0.5/(k**2+(k+x*k)**2)**0.5
    if y<answer:
        answer=y
        myx=x
print(answer,myx)

输出：

0.6180339889095493 0.618

这个总没有问题了吧？还是有问题。你怎么能确定x的区间？

这个问题看似很致命，但并非完全不可解。我们可以大致推断，y的变化趋势应该是先下降后上升或先上升后下降（这个推理对我来说是本能的，以至于我自己都无法详细解释过程，但确实可以推理得到这个结论），而既然是求最小值，那自然是前者。因此，由于x从o.618到1是在增加，所以x一定在0.618或其以下，而这些数显然我们已经遍历到了（至少在某个精度上）。接下来，我们所需要的只是提高精度，以此来得到更接近真实值的结果，并凭借它猜测正确答案。

最终，在较高的精度下（程序与前面大致相同，只是加大了遍历的数值与x缩小的倍数，在此不列出），我们得到结果：

0.6180339887498948 0.618034

我们都知道，黄金分割比的小数点后前65位等于0.6180339887498948482045868343656381177203091798057628621354486227，这个数的前面几位和我们遍历的结果完全吻合。我们有理由相信，答案是黄金分割比(5^0.5-1)/2。于是，我们完美地用Python解决了这个问题。

当然，后来我们老师为我们讲解了这题不需要程序的解决方法：设法将式子中未知部分化为x+a/x的形式，这个式子永远不会小于2a^0.5。这样，我们就可以求得最值了。