game101的透视投影的投影矩阵是这样的



正交投影是这样的

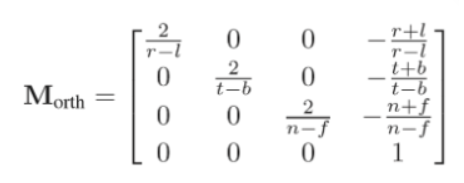
而shader入门精要的透视投影矩阵是这样子



正交投影矩阵是这样子



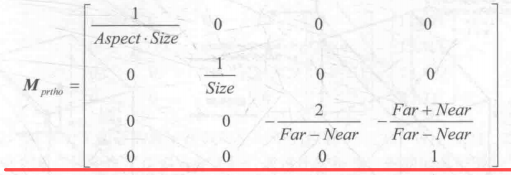
game101的透视投影是这样得到的



而正交投影的时候并没有假设中心点在面的中心



所以区别在于正交投影的时候有没有进行一步位移操作。

可能引起误导的地方

书上投影矩阵这样表示



而101则是认为转换成了正方体，但其实他的w是z，所以按照书上的来看，他也还没有进行归一化。

矩阵最后一行的1乘上z就会导致w变为z。看推导过程也能知道





再来看入门精要。



除了w之后，就当成是一个正方体了。

结论

所以两个在不考虑位移的情况下转换的效果是一样的，都是转换相机坐标得到准备归一化但是还没有归一化的坐标！只是书上画了锥体，games101画的是标准正方体。

《Shader入门精要》中MVP变换的Projection矩阵与《GAMES101图形学入门》中的区别的更多相关文章

  1. （转）思考：矩阵及变换，以及矩阵在DirectX和OpenGL中的运用问题：左乘/右乘,行优先/列优先,...

    转自:http://www.cnblogs.com/soroman/archive/2008/03/21/1115571.html 思考:矩阵及变换,以及矩阵在DirectX和OpenGL中的运用1. ...

  2. 【c语言】二维数组中的查找，杨氏矩阵在一个二维数组中，每行都依照从左到右的递增的顺序排序，输入这种一个数组和一个数，推断数组中是否包括这个数

    // 二维数组中的查找,杨氏矩阵在一个二维数组中.每行都依照从左到右的递增的顺序排序. // 每列都依照从上到下递增的顺序排序.请完毕一个函数,输入这种一个数组和一个数.推断数组中是否包括这个数 #i ...

  3. 《Shader入门精要》第11章-11.3.1流动的河流中的offset.x的解释

    在我学习入门精要的时候,经常遇到不解释api,甚至是关键代码的实现原理. 11.3.1流动的河流中的offset.x的sin函数查了一下好像大家也都是书上原话直接复制,现在好不容易想明白了希望能帮到和 ...

  4. 【C语言】二维数组中的查找，杨氏矩阵

    //二维数组中的查找,杨氏矩阵 //在一个二维数组中,每行都依照从左到右的递增的顺序排序.每列都依照从上到下递增的顺序排序. //请完毕一个函数.输入这种一个数组和一个数,推断数组中是否包括这个数. ...

  5. Unity Shader入门精要学习笔记 - 第16章 Unity中的渲染优化技术

    转自冯乐乐的 <Unity Shader 入门精要> 移动平台的特点 为了尽可能一处那些隐藏的表面,减少overdraw(即一个像素被绘制多次),PowerVR芯片(通常用于ios设备和某 ...

  6. Unity Shader入门精要学习笔记 - 第6章 开始 Unity 中的基础光照

    转自冯乐乐的<Unity Shader入门精要> 通常来讲,我们要模拟真实的光照环境来生成一张图像,需要考虑3种物理现象. 首先,光线从光源中被发射出来. 然后,光线和场景中的一些物体相交 ...

  7. Unity Shader入门精要读书笔记（一）序章

    本系列的博文是笔者读<Unity Shader入门精要>的读书笔记,这本书的章节框架是: 第一章:着手准备. 第二章:GPU流水线. 第三章:Shader基本语法. 第四章:Shader数 ...

  8. Unity Shader入门精要学习笔记 - 第11章 让画面动起来

    转自 冯乐乐的 <Unity Shader入门精要> Unity Shader 中的内置变量 动画效果往往都是把时间添加到一些变量的计算中,以便在时间变化时画面也可以随之变化.Unity ...

  9. Unity Shader入门精要学习笔记 - 第9章 更复杂的光照

    转载自 冯乐乐的<Unity Shader入门精要> Unity 的渲染路径 在Unity里,渲染路径决定了光照是如何应该到Unity Shader 中的.因此,如果要和光源打交道,我们需 ...

随机推荐

  1. uniapp自定义顶部搜索框兼容微信小程序

    zhuanzai:  uniapp自定义顶部搜索框兼容微信小程序 自定义组件 navbarvue (胶囊底部高度 - 状态栏的高度) + (胶囊顶部高度 - 状态栏内的高度) = 导航栏的高度 < ...

  2. UIImageView的frame设置

    - (void)viewDidLoad { [super viewDidLoad]; /* // 设置frame的方式 // 方式一 UIImageView *imageView = [[UIImag ...

  3. 【转】性能测试报告模板 V1.0

    1． 测试项目概述与测试目的 1.1 项目概述  本部分主要是针对即将进行压力测试的对象(接口.模块.进程或系统)进行概要的说明,让人明白该测试对象的主要功能与作用及相关背景. 1.2 测试目标  简 ...

  4. C预备知识_001

    程序由什么构成? 1.对数据的描述:在程序中要指定用到哪些数据以及这些数据的类型和数据的组织形式,其实这就是数据结构(data structure). 2.对操作的描述:即要求计算机就行操作的步骤,也 ...

  5. 项目架构(结构)搭建:主流结构(UITabBarController + 导航控制器)

    /* 项目架构(结构)搭建:主流结构(UITabBarController + 导航控制器) -> 项目开发方式 1.storyboard 2.纯代码 */ @interface AppDele ...

  6. iOS 性能优化系列

    Objective-C 高性能的循环 使用 Swift 和 Objective-C 执行 iOS 内存管理的 7 个简单技巧 @autoreleasepool-内存的分配与释放

  7. [源码解析] NVIDIA HugeCTR，GPU版本参数服务器--- (2)

    [源码解析] NVIDIA HugeCTR,GPU版本参数服务器--- (2) 目录 [源码解析] NVIDIA HugeCTR,GPU版本参数服务器--- (2) 0x00 摘要 0x01 总体流程 ...

  8. Linux源码编译安装php7.2

    以下简单的介绍下如何源码安装PHP,对于版本不一定是7.2,也可以是7.3,当然方法都是换汤不换药的,核心东西不变. 一.下载PHP源码 需要到指定的路径下载源码,执行下面的命令 wget http: ...

  9. 《PHP程序员面试笔试宝典》——如何准备电话面试？

    本文摘自<PHP程序员面试笔试宝典>. PHP面试技巧分享,PHP面试题,PHP宝典尽在"琉忆编程库". 用人单位在收到简历之后,有时候由于求职者众多,而且很多求职者的 ...

  10. Note/Solution -「洛谷 P5158」「模板」多项式快速插值

    \(\mathcal{Description}\)   Link.   给定 \(n\) 个点 \((x_i,y_i)\),求一个不超过 \(n-1\) 次的多项式 \(f(x)\),使得 \(f(x ...