Coprime

Coprime

前置芝士

莫比乌斯反演

正文

首先，我们来分析题意。

题目中给出 \(n\) 个人，每个人有一个编号 \(k\) ，要求我们从中选出 \(3\) 个人，三人编号分别为 \(k_a\) ，\(k_b\) ，\(k_c\) ，

使得这三个人的编号满足两两之间同时互质或不互质，最后求出所有满足上述式子的方案。

我们先来考虑：在什么时候，三个数之间的最小公倍数都相等呢？如果我们朴素一点地计算出答案，那么只要用三层循环，并判断条件是否成立，就可以得到答案。但是，这种朴素算法的时间复杂度为 \(O(n^3)\) ，但题目中的 \(n\) 的范围为 \(10^5\) ，所以这样的时间复杂度显然无法帮助我们拿到这道题的满分。

既然朴素算法的时间复杂度，那该如何更快地计算出这道题的答案呢？我们不妨从容斥的角度来考虑。

首先，从 \(n\) 个人中选出 \(k\) 个人，这表示我们最多能有 \(C_n^3\) 种选人方案。然后，我们随机选出三个人，将选出来的三个人之间两两连边，若两个人的编号互质，则连 ** 蓝边  **，若两人的编号不互质，则连  黄边 ，接着我们会发现，若要符合题目条件，我们只能有以下几种可能：

第一种：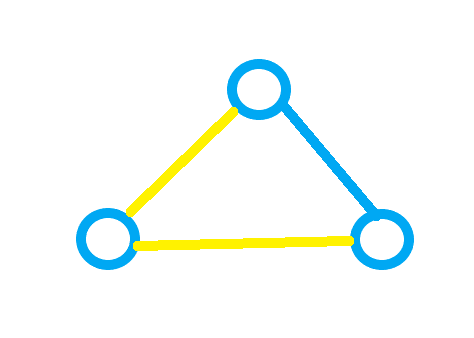

第二种：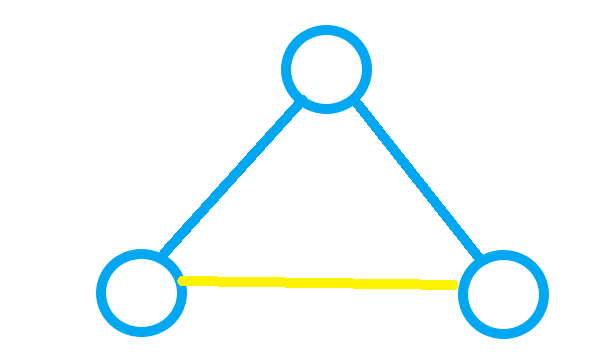

我们会发现两点：第一：最终所得的三角形的个数即为符合条件的方案数。第二：总有两个人身上有两种颜色的边。所以，我们现在定义一个函数 \(f\) ，\(f(i)\)表示与 \(i\) 互质的数有多少个。那么，在计算三角形个数（即总方案数）时，我们就不用再考虑三个人了，而是只要考虑一个人，不过我们在计算时只能取答案的一半，因为身上连有两条不同边的人有两个。

所以，我们有式子：

\[ANS = C_n^3-\frac {\sum_{i=1}^n f(i) (n-i-f(i))}{2}
\]

式中，\(f(i)\) 表示在范围内与 \(i\) 互质的数，所以 \((n-i-f(i))\) 即为范围内与 \(i\) 不互质的数，而 \(n\) 并非题目中的 \(n\) ，而是题目中的 \(a_i\) 的最大值 (即\(10^5\)，接下来我们的 \(n\) 都为 \(10^5\) ）。所以，我们只要能求出全部的 \(f(i)\) ，就可以很快地得到答案了。关于 \(f(i)\) ，我们可以通过下面的方法来处理。

在处理 \(f(i)\) 之前，我们先定义一个数组 \(a\) ，\(a_i\) 则表示数字 \(i\) 在数据中是否存在，若存在，则 \(a_i=1\) ，否则 \(a_i=0\)。然后，再根据我们定义的函数 \(f\) ,可以得到下面的式子：

\[f(x)=\sum_{i=1}^n a_i [GCD(i,x)=1]
\]

这算的便是与 i 互质的数的个数了。我们可以继续加以推导：

\[\begin{align}\\
f(x)&=\sum_{i=1}^n a_i [GCD(i,x)=1]\\
&=\sum_{d|x}\mu(d)\sum_{d|i}^n a_i\\
\end{align}\\
\]

然后我们再定义一个函数 \(g\) ，使得 \(g(d)\) =\(\sum_{d|i}^n a_i\) ，这样我们便可以对 \(g\) 进行预处理，从而降低时间复杂度。

预处理的代码如下：

		for (int i=1; i<=n; i++) {
		      for (int j=i; j<=n; j+=i) g[i]+=a[j];
		}

可见这个预处理的时间复杂度为 \(O(n \log n)\) 。

然后，对于 \(\mu\) 的处理，相信大家做到这道题的时候早就不陌生了，这里就直接采用线性筛的方法（其实没有必要）进行预处理了。然后，我们的 \(f\) 便能直接计算出来。然而，如果我们对每个 \(f\) 单独计算，那么时间复杂度就会变成 \(O(n \sqrt {n})\) ，但只要我们同时计算多个 \(f\) ，那么时间复杂度就会降到 \(O(n\log n)\) （关于时间复杂度的计算，请读者自行思考）。而同时处理多个 \(f\) 的也能很容易的实现，如果说原本我们应该枚举的是 \(x\) 的因数，那现在我们可以通过枚举 \(x\) 的倍数来进行优化。

代码如下：

		for (int i=1; i<=n; i++) {
		      if (mu[i]==0) continue;
		      for (int j=i; j<=n; j+=i) {
			if (a[j]==1) {
			      f[j]+=mu[i]*(g[i]-1);
			}
		      }
		}

最终，我们再将算出来的一切带入最初的式子，就可以计算出答案了。

完整代码如下：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=100005;
int mu[N],prime[N],tot;
bool np[N];
ll f[N],g[N];
bool a[N];
void init(int n) {
	mu[1]=1;
	np[1]=1;
	for (int i=2; i<=n; i++) {
		if (!np[i]) {
			mu[i]=-1;
			prime[tot++]=i;
		}
		for (int j=0,k; (k=prime[j]*i)<=n; j++) {
			np[k]=1;
			if (i%prime[j]==0) {
				mu[k]=0;
				break;
			}
			mu[k]=-mu[i];
		}
	}
}
int main() {
	int T;
	init(100000);
	//cout<<1<<endl;
	scanf("%d",&T);
	for (int _=0; _<T; _++) {
		int n,z;
		scanf("%d",&n);
		z=n;
		memset(g,0,sizeof g);
		memset(f,0,sizeof f);
		memset(a,0,sizeof a);
		ll ans=0;
		for (int i=1; i<=n; i++) {
			int Now;
			scanf("%d",&Now);
			a[Now]=1;
		}
		n=100000;
		for (int i=1; i<=n; i++) {
			for (int j=i; j<=n; j+=i) g[i]+=a[j];
		}
		for (int i=1; i<=n; i++) {
			if (mu[i]==0) continue;//优化
				for (int j=i; j<=n; j+=i) {
					if (a[j]==1) {
						f[j]+=mu[i]*(g[i]-1);
					}
				}
		}
		for (int i=1;i<=n;i++) ans=ans+f[i]*(z-1-f[i]);
		ans=(ll)z*(z-1)*(z-2)/6-ans/2;
		printf("%lld\n",ans);
	}
	return 0;
}