【十大经典数据挖掘算法】k-means

【十大经典数据挖掘算法】系列

1. C4.5
2. K-Means
3. SVM
4. Apriori
5. EM
6. PageRank
7. AdaBoost
8. kNN
9. Naïve Bayes
10. CART

---

1. 引言

k-means与kNN虽然都是以k打头，但却是两类算法——kNN为监督学习中的分类算法，而k-means则是非监督学习中的聚类算法；二者相同之处：均利用近邻信息来标注类别。

聚类是数据挖掘中一种非常重要的学习流派，指将未标注的样本数据中相似的分为同一类，正所谓“物以类聚，人以群分”嘛。k-means是聚类算法中最为简单、高效的，核心思想：由用户指定k个初始质心（initial centroids)，以作为聚类的类别（cluster），重复迭代直至算法收敛。

2. 基本算法

在k-means算法中，用质心来表示cluster；且容易证明k-means算法收敛等同于所有质心不再发生变化。基本的k-means算法流程如下：

选取k个初始质心（作为初始cluster）；
repeat：
    对每个样本点，计算得到距其最近的质心，将其类别标为该质心所对应的cluster；
    重新计算k个cluser对应的质心；
until 质心不再发生变化

对于欧式空间的样本数据，以平方误差和（sum of the squared error, SSE)作为聚类的目标函数，同时也可以衡量不同聚类结果好坏的指标：

\[SSE=\sum\limits_{i=1}^{k} \sum_{x\in C_{i}} dist(x, c_i)
\]

表示样本点\(x\)到cluster \(C_i\) 的质心 \(c_i\) 距离平方和；最优的聚类结果应使得SSE达到最小值。

下图中给出了一个通过4次迭代聚类3个cluster的例子：

k-means存在缺点：

• k-means是局部最优的，容易受到初始质心的影响；比如在下图中，因选择初始质心不恰当而造成次优的聚类结果（SSE较大）：
  
  

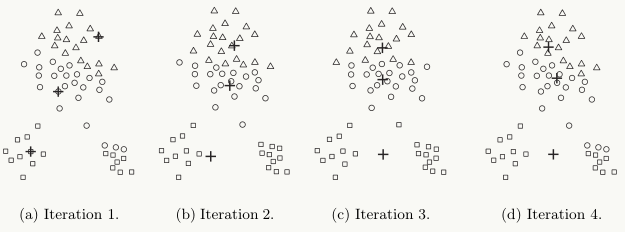
• 同时，k值的选取也会直接影响聚类结果，最优聚类的k值应与样本数据本身的结构信息相吻合，而这种结构信息是很难去掌握，因此选取最优k值是非常困难的。

3. 优化

为了解决上述存在缺点，在基本k-means的基础上发展而来二分 (bisecting) k-means，其主要思想：一个大cluster进行分裂后可以得到两个小的cluster；为了得到k个cluster，可进行k-1次分裂。算法流程如下：

初始只有一个cluster包含所有样本点；
repeat:
    从待分裂的clusters中选择一个进行二元分裂，所选的cluster应使得SSE最小；
until 有k个cluster

上述算法流程中，为从待分裂的clusters中求得局部最优解，可以采取暴力方法：依次对每个待分裂的cluster进行二元分裂（bisect）以求得最优分裂。二分k-means算法聚类过程如图：

从图中，我们观察到：二分k-means算法对初始质心的选择不太敏感，因为初始时只选择一个质心。

4. 参考资料

[1] Pang-Ning Tan, Michael Steinbach, Vipin Kumar, Introduction to Data Mining.

[2] Xindong Wu, Vipin Kumar, The Top Ten Algorithms in Data Mining.