机器学习--主成分分析(PCA)算法的原理及优缺点

一、PCA算法的原理

　　PCA（principle component analysis），即主成分分析法，是一个非监督的机器学习算法，是一种用于探索高维数据结构的技术，主要用于对数据的降维，通过降维可以发现更便于人理解的特征，加快对样本有价值信息的处理速度，此外还可以应用于可视化（降到二维）和去噪。

　　1、PCA与LDA算法的基本思想

　　数据从原来的坐标系转换到新的坐标系，新坐标系的选择是由数据本身决定的。第一个新坐标轴选择的是原始数据中方差最大的方向，第二个新坐标轴选择和第一个坐标轴正交且具有最大方差的方向。该过程一直重复，重复次数为原始数据中特征的数目。我们会发现，大部分方差都包含在最前面的几个新坐标轴中。因此，我们可以忽略余下的坐标轴，即对数据进行降维处理。

　　2、数学推导过程

　　PCA本质上是将方差最大的方向作为主要特征，并且在各个正交方向上将数据“离相关”，也就是让它们在不同正交方向上没有相关性。

                                      

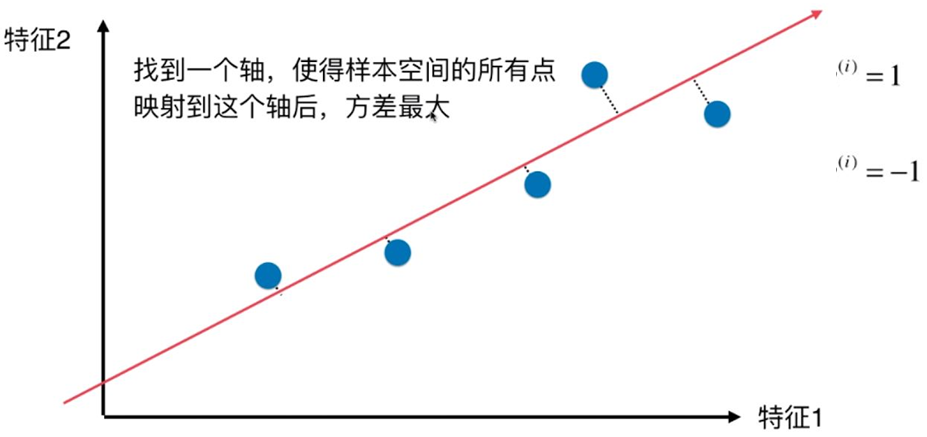
　　求解思路：用方差来定义样本的间距，方差越大表示样本分布越稀疏，方差越小表示样本分布越密集。

　　方差的公式如下：

　　　　　　

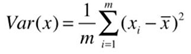
　　　　在求解最大方差前，为了方便计算，可以先对样本进行demean（去均值）处理，即减去每个特征的均值，这种处理方式不会改变样本的相对分布（效果就像坐标轴进行了移动）。去均值后，样本x每个特征维度上的均值都是0，方差的公式转换下图的公式：

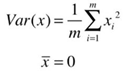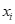　　　　　　                                                                                               在这里，代表已经经过映射后的某样本。

　　　　对于只有2个维度的样本，现在的目标就是：求一个轴的方向w=（w1,w2），使得映射到w方向后，方差最大。

　　　　目标函数表示如下：

　　　　　　    

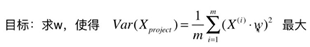
　　　　为求解此问题，需要使用梯度上升算法，梯度的求解公式如下：

　　　　　　                                  

　　　3、PCA算法流程:　　　

　　　　（1）去平均值，即每一位特征减去各自的平均值；

　　　　（2）计算协方差矩阵；

　　　　（3）计算协方差矩阵的特征值与特征向量；

　　　　（4）对特征值从大到小排序；

　　　　（5）保留最大的个特征向量；

　　　　（6）将数据转换到个特征向量构建的新空间中。

　　4、PCA算法实现一般流程：　　　　　

　　　　  （1）对数据进行归一化处理；

　　　　（2）计算归一化后的数据集的协方差矩阵；

　　　　（3）计算协方差矩阵的特征值和特征向量；

　　　　（4）保留最重要的k个特征（通常k要小于n）；

　　　　（5）找出k个特征值相应的特征向量

　　　　（6）将m * n的数据集乘以k个n维的特征向量的特征向量（n * k）,得到最后降维的数据。

　　5、PCA降维准则：

　　　　（1） 最近重构性：样本集中所有点，重构后的点距离原来的点的误差之和最小。

　　　　（2） 最大可分性：样本在低维空间的投影尽可能分开。

　　6、PCA算法优点：

　　         （1）使得数据集更易使用；

　　　　（2）降低算法的计算开销；

　　　　（3）去除噪声；

　　　　（4）使得结果容易理解；

　　　　（5）完全无参数限制。

　　7、PCA算法缺点：

　　　　（1）如果用户对观测对象有一定的先验知识，掌握了数据的一些特征，却无法通过参数化等方法对处理过程进行干预，可能会得不到预期的效果，效率也不高；

　　　　（2） 特征值分解有一些局限性，比如变换的矩阵必须是方阵；

　　　　（3） 在非高斯分布情况下，PCA方法得出的主元可能并不是最优的。

　　8、PCA算法应用：

　　　　（1）高维数据集的探索与可视化。

　　　　（2）数据压缩。

　　　　（3）数据预处理。

　　　　（4）图象、语音、通信的分析处理。

　　　　（5）降维(最主要)，去除数据冗余与噪声。

二、代码实现

　　1.自己实现的PCA算法（不使用sklearn）

import numpy as np
import matplotlib.pyplot as plt

X=np.empty((100,2))
X[:,0]=np.random.uniform(0,100,size=100)
X[:,1]=0.75*X[:,0]+3+np.random.normal(0,10,size=100)
plt.scatter(X[:,0],X[:,1])

def demean(X):
    return X-np.mean(X,axis=0)
X_demean=demean(X)
plt.figure(2)
plt.scatter(X_demean[:,0],X_demean[:,1])
#print(np.mean(X[:,0]))
#print(np.mean(X_deman[:,0]))
#print(np.mean(X_deman[:,1]))

def f(w,X):
    return np.sum((X.dot(w)**2))/len(X)

def df_math(w,X):
    return X.T.dot(X.dot(w))*2/len(X)

def direction(w):
    return w / np.linalg.norm(w)

def gradient_ascent(df, X, initial_w, eta, n_iters = 1e4, epsilon=1e-8):

    w = direction(initial_w)
    cur_iter = 0

    while cur_iter < n_iters:
        gradient = df(w, X)
        last_w = w
        w = w + eta * gradient
        w = direction(w) # 注意1：每次求一个单位方向
        if(abs(f(w, X) - f(last_w, X)) < epsilon):
            break

        cur_iter += 1

    return w

initial_w = np.random.random(X.shape[1]) # 注意2：不能用0向量开始
eta = 0.001
w = gradient_ascent(df_math, X_demean, initial_w, eta)
plt.figure(3)
plt.scatter(X_demean[:,0], X_demean[:,1])
#plt.plot([0, w[0]*30], [0, w[1]*30], color='r')
plt.plot([0, w[0]*50], [0 , w[1]*50], color='r')

　输出结果：



　　 2、PCA分类

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

#计算均值,要求输入数据为numpy的矩阵格式，行表示样本数，列表示特征
def meanX(dataX):
    return np.mean(dataX,axis=0)#axis=0表示依照列来求均值。假设输入list,则axis=1
"""
參数：
    - XMat：传入的是一个numpy的矩阵格式，行表示样本数，列表示特征
    - k：表示取前k个特征值相应的特征向量
返回值：
    - finalData：參数一指的是返回的低维矩阵，相应于输入參数二
    - reconData：參数二相应的是移动坐标轴后的矩阵
"""
def pca(XMat, k):
    average = meanX(XMat)
    m, n = np.shape(XMat)
    data_adjust = []
    avgs = np.tile(average, (m, 1))
    data_adjust = XMat - avgs
    covX = np.cov(data_adjust.T)   #计算协方差矩阵
    featValue, featVec=  np.linalg.eig(covX)  #求解协方差矩阵的特征值和特征向量
    index = np.argsort(-featValue) #依照featValue进行从大到小排序
    finalData = []
    if k > n:
        print("k must lower than feature number")
        return
    else:
        #注意特征向量时列向量。而numpy的二维矩阵(数组)a[m][n]中，a[1]表示第1行值
        selectVec = np.matrix(featVec.T[index[:k]]) #所以这里须要进行转置
        finalData = data_adjust * selectVec.T
        reconData = (finalData * selectVec) + average
    return finalData, reconData

#输入文件的每行数据都以\t隔开
def loaddata(datafile):
    return np.array(pd.read_csv(datafile,sep=" ",header=-1)).astype(np.float)
def plotBestFit(data1, data2):
    dataArr1 = np.array(data1)
    dataArr2 = np.array(data2)

    m = np.shape(dataArr1)[0]
    axis_x1 = []
    axis_y1 = []
    axis_x2 = []
    axis_y2 = []
    for i in range(m):
        axis_x1.append(dataArr1[i,0])
        axis_y1.append(dataArr1[i,1])
        axis_x2.append(dataArr2[i,0])
        axis_y2.append(dataArr2[i,1])
    fig = plt.figure()
    ax = fig.add_subplot(111)
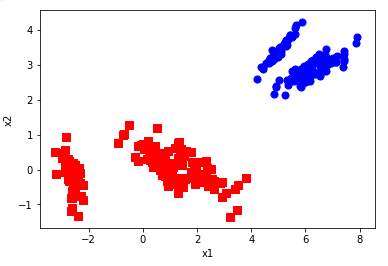
    ax.scatter(axis_x1, axis_y1, s=50, c='red', marker='s')
    ax.scatter(axis_x2, axis_y2, s=50, c='blue')
    plt.xlabel('x1'); plt.ylabel('x2');
    plt.savefig("outfile.png")
    plt.show()  
#依据数据集data.txt
def main():
    datafile = "data.txt"
    XMat = loaddata(datafile)
    k = 2
    return pca(XMat, k)
if __name__ == "__main__":
    finalData, reconMat = main()
    plotBestFit(finalData, reconMat)

运行结果：