【最小生成树之Prim算法】-C++

【最小生成树之Kruskal算法】
没有看过的可以先看↑，会更简单。
【模板】最小生成树
这一篇博客主要是介绍另外一种算法：Prim算法。
prim算法就好像是一棵"生成树"在慢慢长大，从开始的一个顶点长到了n个顶点。
总结一下这个算法，将图中所有的顶点分为2类，树顶点（已被选入生成树的顶点）和非树顶点（还未被选入生成树的顶点），接下来要找出一条边添加到生成树，这需要枚举每一个树顶点到每一个非树顶点所有的边，然后最短边加入到生成树，重复操作n-1次，直到所有顶点加入到生成树中。
实现此算法时，比较了dijkstra最短路径算法，在记录的最短距离，不是每个顶点到1号顶点的距离，而是每个顶点到任意一个“树顶点”的最短距离。
时间复杂度：O(n^2)（n为顶点数）
主要思路： 通过依次加入新的最优的店来实现。用dst[i]来表示第i个点加入这棵树所需的代价。
可能有点难理解，那就画图理解：
大概如下一个无向图：

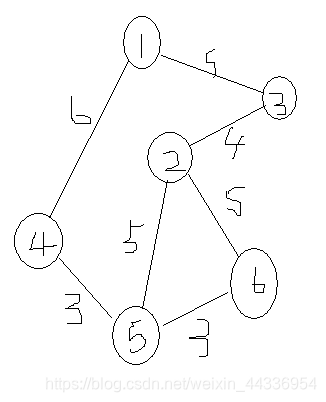
因为从任意一个顶点出发都可以生成这棵最小数，所以我们在代码中都规定从编号为1的定点开始构造。（将1打上标记）同时记录dst[1]=0;（是没有任何代价的，可以自己理解一下）

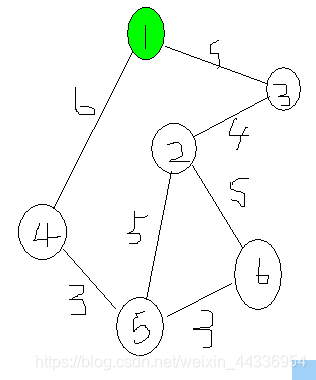
从点1出发，我们可以找到（和点1直接连接的点）有3和4，选择边权值最小的一个（1-3）那么将3也放进已经确定来源的部分（打标记）如下（同时记录dst[3]=5;）

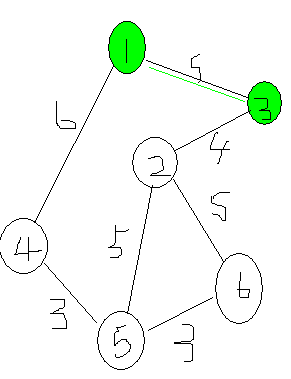
和3有连接的点只有2，那么也打上标记.（记录dst[2]=4）

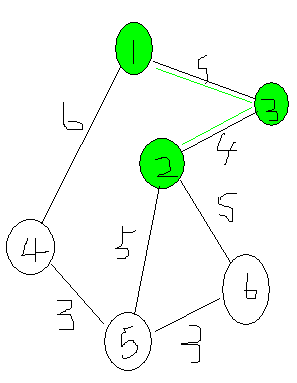
按照循环顺序，应该先找到5（记录dst[5]=5）

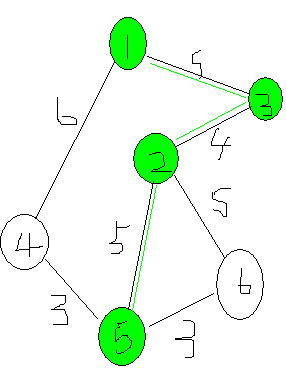
接下来找到4（记录dst[4]=3）

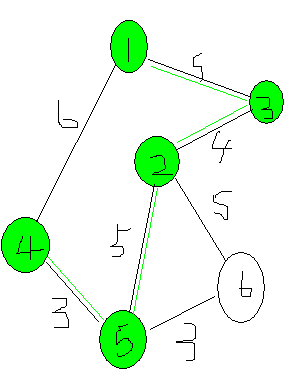
接下来找到点6（记录dst[6]=3（这样最优）)

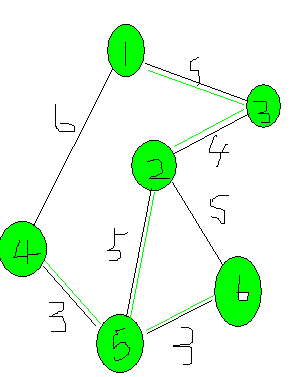
这样，每个点都加入了这棵树，所以任务完成，这棵树的最小生成树形态如下：

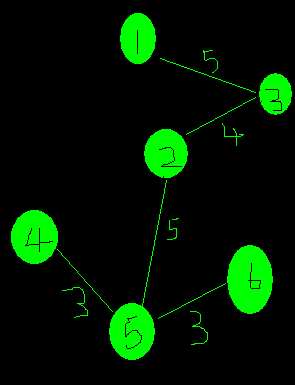
接下来说说代码实现。
根据我们的模拟过程，输入之后先将点1打上标记，然后在和点1有连接的所有点中找到最优点3，然后将点3打上标记，然后在和点3有连接的所有点中找到最优点2.。。。。。
发现过程规律了吗?双重循环即可解决这个问题！
我们用一个结构体+二维vector数组g来记录与点i相连的所有点及其权值。另外为了方便，我还是用pre[i]来表示是点pre[i]连接上点i进入这棵树的。
外层for(i=1->n-1)内层第一个for(j=0->g[lasti].size())确定当前每个点的最优代价（不断更新）内层第二个for(i=1->n)统计最优点即可。

代码如下:

#include<bits/stdc++.h>
using namespace std;
int dst[5010];
int n,m;
bool s[5010];
int pre[5010];
struct node
{
    int v,w;
    node(){}
    node(int vv,int ww)
    {
        v=vv,w=ww;
    }
};
vector<node> g[5010];
void init()
{
    for(int i=1;i<=5000;i++)
    {
        dst[i]=0x7f7f7f7f;
    }
}
int main()
{
    init();
    int a,b,c;
    cin>>n>>m;
    for(int i=1;i<=m;i++)
    {
        cin>>a>>b>>c;
        g[a].push_back(node(b,c));
        g[b].push_back(node(a,c));
    }
    s[1]=1;
    dst[1]=0;
    int lasti=1;
    for(int k=1;k<n;k++)
    {
        for(int j=0;j<g[lasti].size();j++)
        {
            int v=g[lasti][j].v,w=g[lasti][j].w;
            if(!s[v]&&w<dst[v])
            {
                pre[v]=lasti;
                dst[v]=w;
                //dst[v]+=dst[pre[v]];
            }
        }
        int min_i=0x7f7f7f7f,min_dst=0x7f7f7f7f;
        for(int i=1;i<=n;i++)
        {
            if(!s[i])
            {
                if(dst[i]<min_dst)
                {
                    min_dst=dst[i];
                    min_i=i;
                }
            }
        }
        lasti=min_i;
        s[min_i]=1;
        printf("更新点%d加入，父节点%d\n",lasti,pre[lasti]);
    }

    int total=0;
    for(int i=1;i<=n;i++)
    {
        total+=dst[i];
        printf("pre[%d]=%d\n",i,pre[i]);
    }
    cout<<total<<endl;
    return 0;
}

输入如下数据:

6 7
1 3 5
3 2 4
2 6 5
2 5 5
5 6 3
4 5 3
1 4 6

输出如下:

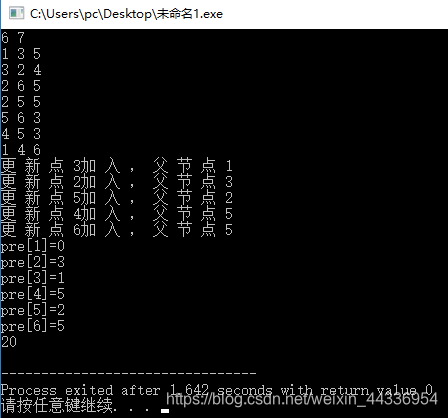
prim算法要嗦的大概就是这些，剩下的需要自己不断理解，希望大家在这条路上越走越远，加油!
ov.