myql忽略大小写问题解决

linux系统下启动mysql默认是区分大小写的，如果刚好项目中使用的表名与数据库中表名大小写有冲突，此时就需要忽略mysql表名大小写了。

解决方式一：

1.关闭数据库

mysqladmin -uroot -p shutdown

->输入数据库密码。

2.修改配置文件my.cnf

vi /etc/my.cnf

2.添加忽略mysql表名大小写配置参数

lower_case_table_names=

如图：

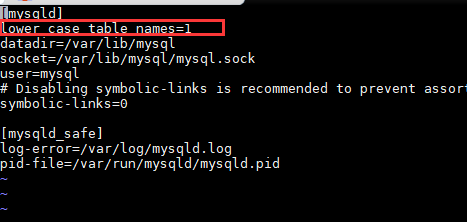
3.启动数据库

service mysqld start

完成！