集合系列 Map（十五）：TreeMap

TreeMap 是 Map 集合的有序实现，其底层是基于红黑树的实现，能够早 log(n) 时间内完成 get、put 和 remove 操作。

public class TreeMap<K,V>
    extends AbstractMap<K,V>
    implements NavigableMap<K,V>, Cloneable, java.io.Serializable

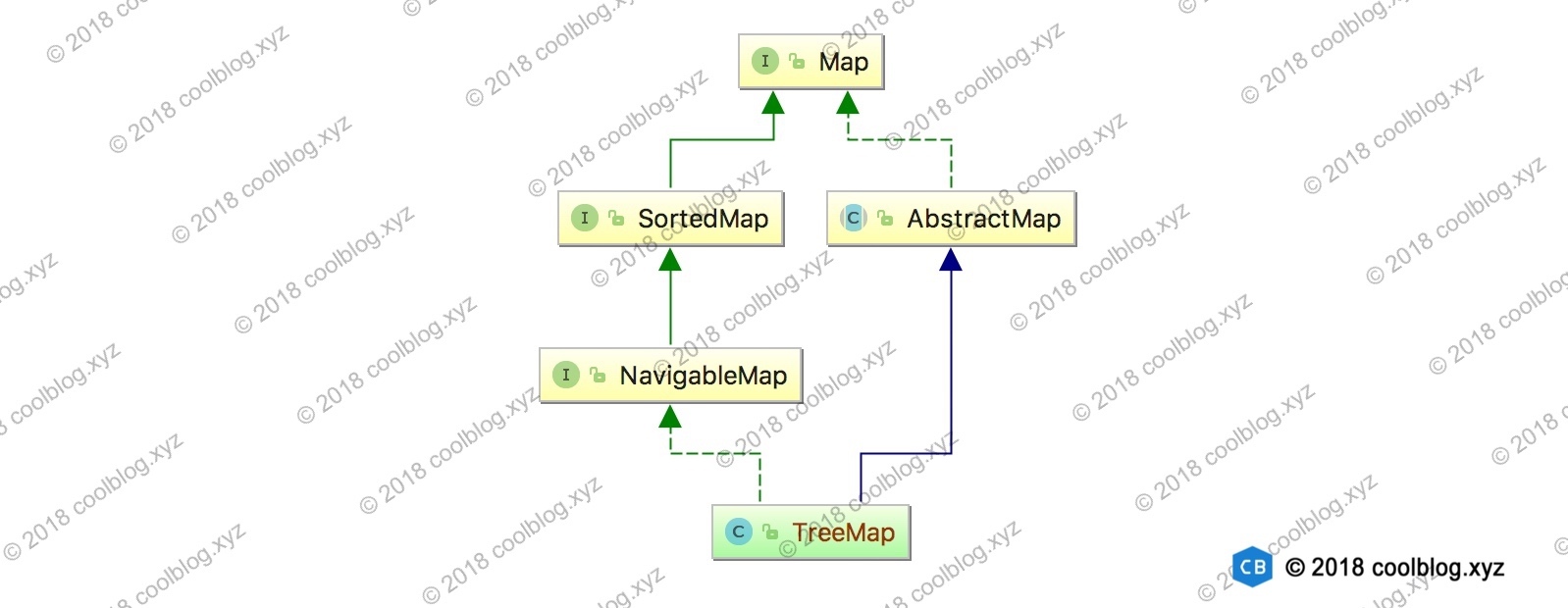
TreeMap 继承自 AbstractMap，还实现了 NavigableMap接口。NavigableMap 接口继承了SortedMap接口，SortedMap 最终继承自Map接口。整体来说 TreeMap 的继承体系如下图所示。

原理

我们将从类成员变量、构造方法、核心方法几个方面来解析 TreeMap 的实现。

类成员变量

// 比较器。根据这个比较器决定TreeMap的排序。
// 如果为空，表示按照key做自然排序（最小的在根节点）。
private final Comparator<? super K> comparator;
// 根节点
private transient Entry<K,V> root;
// 大小
private transient int size = 0;
// Node节点声明
static final class Entry<K,V> implements Map.Entry<K,V> {
    K key;
    V value;
    Entry<K,V> left;
    Entry<K,V> right;
    Entry<K,V> parent;
    boolean color = BLACK;
}

我们可以看到 TreeMap 有一个 Entry 类型的 root 节点，而 Entry 则是 TreeMap 的内部类。从 TreeMap.Entry 的属性我们可以知道其实一个红黑树节点的实现。

构造方法

TeeMap 一共有四个构造方法：

public TreeMap() {
    comparator = null;
}

public TreeMap(Comparator<? super K> comparator) {
    this.comparator = comparator;
}

public TreeMap(Map<? extends K, ? extends V> m) {
    comparator = null;
    putAll(m);
}

public TreeMap(SortedMap<K, ? extends V> m) {
    comparator = m.comparator();
    try {
        buildFromSorted(m.size(), m.entrySet().iterator(), null, null);
    } catch (java.io.IOException cannotHappen) {
    } catch (ClassNotFoundException cannotHappen) {
    }
}

核心方法

我们将从查找、插入、删除、遍历四个方法研究 TreeMap 的实现。

查找

TreeMap基于红黑树实现，而红黑树是一种自平衡二叉查找树，所以 TreeMap 的查找操作流程和二叉查找树一致。二叉树的查找流程是这样的，先将目标值和根节点的值进行比较，如果目标值小于根节点的值，则再和根节点的左孩子进行比较。如果目标值大于根节点的值，则继续和根节点的右孩子比较。在查找过程中，如果目标值和二叉树中的某个节点值相等，则返回 true，否则返回 false。

TreeMap 查找和此类似，只不过在 TreeMap 中，节点（Entry）存储的是键值对<k,v>。在查找过程中，比较的是键的大小，返回的是值，如果没找到，则返回null。TreeMap 中的查找方法是get，具体实现在getEntry方法中，相关源码如下：

public V get(Object key) {
    Entry<K,V> p = getEntry(key);
    return (p==null ? null : p.value);
}

final Entry<K,V> getEntry(Object key) {
    // Offload comparator-based version for sake of performance
    if (comparator != null)
        return getEntryUsingComparator(key);
    if (key == null)
        throw new NullPointerException();
    @SuppressWarnings("unchecked")
        Comparable<? super K> k = (Comparable<? super K>) key;
    Entry<K,V> p = root;
    // 核心查找逻辑
    while (p != null) {
        int cmp = k.compareTo(p.key);
        if (cmp < 0)
            p = p.left;
        else if (cmp > 0)
            p = p.right;
        else
            return p;
    }
    return null;
}

插入

TreeMap 的插入其实就是红黑树的插入，因此搞懂了红黑树插入的各个情况，看懂 TreeMap 的插入源码就不在话下了。

public V put(K key, V value) {
    Entry<K,V> t = root;
    // 1. 如果根节点为 null，将新节点设为根节点
    if (t == null) {
        compare(key, key); // type (and possibly null) check
        root = new Entry<>(key, value, null);
        size = 1;
        modCount++;
        return null;
    }
    int cmp;
    Entry<K,V> parent;
    // 2.为 key 在红黑树找到合适的位置
    Comparator<? super K> cpr = comparator;
    if (cpr != null) {

        do {
            parent = t;
            cmp = cpr.compare(key, t.key);
            if (cmp < 0)
                t = t.left;
            else if (cmp > 0)
                t = t.right;
            else
                return t.setValue(value);
        } while (t != null);
    }
    else {
        if (key == null)
            throw new NullPointerException();
        @SuppressWarnings("unchecked")
            Comparable<? super K> k = (Comparable<? super K>) key;
        do {
            parent = t;
            cmp = k.compareTo(t.key);
            if (cmp < 0)
                t = t.left;
            else if (cmp > 0)
                t = t.right;
            else
                return t.setValue(value);
        } while (t != null);
    }
    // 3.将新节点链入红黑树中
    Entry<K,V> e = new Entry<>(key, value, parent);
    if (cmp < 0)
        parent.left = e;
    else
        parent.right = e;
    // 4.插入新节点可能会破坏红黑树性质，这里修正一下
    fixAfterInsertion(e);
    size++;
    modCount++;
    return null;
}

删除

TreeMap 的删除其实就是红黑树的删除，因此搞懂了红黑树删除的各个情况，看懂 TreeMap 的删除源码就不在话下了。

public V remove(Object key) {
    Entry<K,V> p = getEntry(key);
    if (p == null)
        return null;

    V oldValue = p.value;
    deleteEntry(p);
    return oldValue;
}

private void deleteEntry(Entry<K,V> p) {
    modCount++;
    size--;

    /*
     * 1. 如果 p 有两个孩子节点，则找到后继节点，
     * 并把后继节点的值复制到节点 P 中，并让 p 指向其后继节点
     */
    if (p.left != null && p.right != null) {
        Entry<K,V> s = successor(p);
        p.key = s.key;
        p.value = s.value;
        p = s;
    } // p has 2 children

    // Start fixup at replacement node, if it exists.
    Entry<K,V> replacement = (p.left != null ? p.left : p.right);

    if (replacement != null) {
        /*
         * 2. 将 replacement parent 引用指向新的父节点，
         * 同时让新的父节点指向 replacement。
         */
        replacement.parent = p.parent;
        if (p.parent == null)
            root = replacement;
        else if (p == p.parent.left)
            p.parent.left  = replacement;
        else
            p.parent.right = replacement;

        // Null out links so they are OK to use by fixAfterDeletion.
        p.left = p.right = p.parent = null;

        // 3. 如果删除的节点 p 是黑色节点，则需要进行调整
        if (p.color == BLACK)
            fixAfterDeletion(replacement);
    } else if (p.parent == null) { // 删除的是根节点，且树中当前只有一个节点
        root = null;
    } else { // 删除的节点没有孩子节点
        // p 是黑色，则需要进行调整
        if (p.color == BLACK)
            fixAfterDeletion(p);

        // 将 P 从树中移除
        if (p.parent != null) {
            if (p == p.parent.left)
                p.parent.left = null;
            else if (p == p.parent.right)
                p.parent.right = null;
            p.parent = null;
        }
    }
}

遍历

TreeMap 有一个特性，即可以保证键的有序性，默认是正序。所以在遍历过程中，大家会发现 TreeMap 会从小到大输出键的值。那么，接下来就来分析一下keySet方法，以及在遍历 keySet 方法产生的集合时，TreeMap 是如何保证键的有序性的。相关代码如下：

public Set<K> keySet() {
    return navigableKeySet();
}

public NavigableSet<K> navigableKeySet() {
    KeySet<K> nks = navigableKeySet;
    return (nks != null) ? nks : (navigableKeySet = new KeySet<>(this));
}

static final class KeySet<E> extends AbstractSet<E> implements NavigableSet<E> {
    private final NavigableMap<E, ?> m;
    KeySet(NavigableMap<E,?> map) { m = map; }

    public Iterator<E> iterator() {
        if (m instanceof TreeMap)
            return ((TreeMap<E,?>)m).keyIterator();
        else
            return ((TreeMap.NavigableSubMap<E,?>)m).keyIterator();
    }

    // 省略非关键代码
}

Iterator<K> keyIterator() {
    return new KeyIterator(getFirstEntry());
}

final class KeyIterator extends PrivateEntryIterator<K> {
    KeyIterator(Entry<K,V> first) {
        super(first);
    }
    public K next() {
        return nextEntry().key;
    }
}

abstract class PrivateEntryIterator<T> implements Iterator<T> {
    Entry<K,V> next;
    Entry<K,V> lastReturned;
    int expectedModCount;

    PrivateEntryIterator(Entry<K,V> first) {
        expectedModCount = modCount;
        lastReturned = null;
        next = first;
    }

    public final boolean hasNext() {
        return next != null;
    }

    final Entry<K,V> nextEntry() {
        Entry<K,V> e = next;
        if (e == null)
            throw new NoSuchElementException();
        if (modCount != expectedModCount)
            throw new ConcurrentModificationException();
        // 寻找节点 e 的后继节点
        next = successor(e);
        lastReturned = e;
        return e;
    }

    // 其他方法省略
}

上面的代码比较多，keySet 涉及的代码还是比较多的，大家可以从上往下看。从上面源码可以看出 keySet 方法返回的是 KeySet 类的对象。这个类实现了Iterable接口，可以返回一个迭代器。该迭代器的具体实现是 KeyIterator，而 KeyIterator 类的核心逻辑是在PrivateEntryIterator中实现的。上面的代码虽多，但核心代码还是 KeySet 类和 PrivateEntryIterator 类的 nextEntry方法。KeySet 类就是一个集合，这里不分析了。而 nextEntry 方法比较重要，下面简单分析一下。

在初始化 KeyIterator 时，默认情况下会将 TreeMap 中包含最小键或最大值（取决于传入的比较器）的 Entry 传给 PrivateEntryIterator。当调用 nextEntry 方法时，通过调用 successor 方法找到当前 entry 的后继，并让 next 指向后继，最后返回当前的 entry。通过这种方式即可实现按正序返回键值的的逻辑。

总结

TreeMap 是 Map 集合的经典红黑树实现，所以弄懂了红黑树的查询、插入、删除，TreeMap 的源码自然不再话下。但要注意的是，TreeMap 的遍历并不是从根节点开始遍历，而是根据 key 的大小从小到大输出，或者从大到小输出。到底是升序还是降序，取决于传入的 Comparator，默认是升序，即从小到大输出。

• TreeMap 是哈希的红黑树经典实现，是Map的哈希有序实现。