【学习笔记】动态规划—各种 DP 优化

【大前言】

个人认为贪心，$dp$ 是最难的，每次遇到题完全不知道该怎么办，看了题解后又瞬间恍然大悟（TAT）。这篇文章也是花了我差不多一个月时间才全部完成。

【进入正题】

用动态规划解决问题具有空间耗费大、时间效率高的特点，但也会有时间效率不能满足要求的时候，如果算法有可以优化的余地，就可以考虑时间效率的优化。

【DP 时间复杂度的分析】

$DP$ 高时间效率的关键在于它减少了“冗余”，即不必要的计算或重复计算部分，算法的冗余程度是决定算法效率的关键。而动态规划就是在将问题规模不断缩小的同时，记录已经求解过的子问题的解，充分利用求解结果，避免了反复求解同一子问题的现象，从而减少“冗余”。

但是，一个动态规划问题很难做到完全消除“冗余”。

下面给出动态规划时间复杂度的决定因素：

时间复杂度 $=$ 状态总数 $×$ 每个状态转移的状态数 $×$ 每次状态转移的时间

【DP 优化思路】

一：减少状态总数

$(1).$ 改进状态表示

$(2).$选择适当的规划方向

二：减少每个状态转移的状态数

$(1).$ 四边形不等式和决策的单调性

$(2).$ 决策量的优化

$(3).$ 合理组织状态

$(4).$ 细化状态转移

三：减少状态转移的时间

$(1).$ 减少决策时间

$(2).$ 减少计算递推式的时间

（上述内容摘自 《动态规划算法的优化技巧》毛子青 ，想要深入了解其思想的可以去看看这篇写得超级好的论文。）

看到这里是不是已经感觉有点蒙了呢？

本蒟蒻总结了一个简化版本：

【DP 三要点】

在推导 $dp$ 方程时，我们时常会感到毫无头绪，而实际上 $dp$ 方程也是有迹可循的，总的来说，需要关注两个要点：状态，决策和转移。其中 “状态” 又最为关键，决策最为复杂。

【状态】

关于 “状态” 的优化可以从很多角度出发，思维难度及其高，有时候状态选择的好坏会直接导致出现暴零和满分的分化。

【决策】

与 “状态” 不同，“决策” 优化则有着大量模板化的东西，在各大书籍，文章上你都可以看到这样的话：只要是形如 $XXX$ 的状态转移方程，都可以用 $XXX$ 进行优化。

【转移】

“转移” 则指由最优决策点得到答案的转移过程，其复杂度一般较低，通常可以忽略，但有时也需要特别注意并作优化。

本文将会重点针对 “决策” 优化部分作一些总结，记录自己的感悟和理解。

\[QAQ
\]

一：【矩阵优化 DP】

$updata$ 之后由于篇幅过大，已搬出。。。。。

【学习笔记】动态规划—矩阵递推加速

补充：其实质是优化 “转移”。

\[QAQ
\]

二：【数据结构优化 DP】

【前言】

在一些 $dp$ 方程的状态转移过程中，我们通常需要在某个范围内进行择优，选出最佳决策点，这往往可以作为 $dp$ 优化的突破口。

数据结构的使用较灵活，没有一个特定的模板，需要根据具体情况而定，选择合适的方案。由于状态转移总是伴随着区间查询最值，区间求和等操作，即动态区间操作，所以平衡树可以作为一个有用的工具，但考虑到代码复杂度，使用树状数组或者线段树将会是一个不错的选择。。

其实质是优化 “决策”。

1.【维护合适的信息】

以 $The$ $Battle$ $of$ $Chibi$ $[UVA12983]$ 为例，大概题意就是计算在给定的序列中严格单调递增子序列的数量，并对 $1e9
+7$ 取模，给定序列长度小于等于 $1000$ 。

方程应该是比较好推的，用 $dp[i][j]$ 表示由序列中在 $j$ 之前的数构成并以 $a[j]$ 结尾的子序列中，长度为 $i$ 的子序列的数量。则：$dp[i][j]=\sum dp[i-1][k]$ ，其中 $k < j$ $且$ $a[k] < a[j]$ 。

对于决策点 $dp[i-1][k]$ 这里出现了 $3$ 个信息：

$(1).$ 在原序列中的位置 $k<j$ 。

$(2).$ $a[k]<a[j]$ 。

$(3).$ $dp[i-1][k]$ 的和。

对于 $(1)$，可以用枚举的顺序解决，剩下的两个信息即是数据结构需要维护的信息。

对于每一次 $dp[i]$ 的决策，可以将 $a[j]$ 作为数据结构维护的关键字， $dp[i-1][j]$ 作为权值，加入 $-inf$ 后离散化，得到一个大小为 $N+1$ 的数组并在上面建立树状数组，每次计算 $dp[i][j]$ 时查询前面已经加入的且关键字小于 $a[j]$ 的 $dp[i-1][k]$ 总和（即区间查询），然后把 $dp[i-1][j]$ 加入树状数组（单点查询）。

时间复杂度为 $O(logn)$。

当问题涉及到的操作更复杂时，树状数组无法维护所需要的信息，就只有用线段树了。这道题较简单，所以选择了代码复杂度更低的树状数组。

2.【Code】

#include<algorithm>

#include<cstring>

#include<cstdlib>//UVA抽风，加上这个就好了

#include<cstdio>

#define Re register int

using namespace std;//UVA抽风，还要加这个

const int N=1005,P=1e9+7;

int n,m,T,k,ans,cnt,a[N],b[N],C[N],dp[N][N];

inline void add(Re x,Re v){while(x<=n+1)(C[x]+=v)%=P,x+=x&-x;}

inline int ask(Re x){Re ans=0;while(x)(ans+=C[x])%=P,x-=x&-x;return ans%P;}

int main(){

    scanf("%d",&T);

    for(Re o=1;o<=T;++o){

        scanf("%d%d",&n,&m),ans=0,cnt=n;

        memset(dp,0,sizeof(dp));

        for(Re i=1;i<=n;++i)scanf("%d",&a[i]),b[i]=a[i],dp[1][i]=1;

        sort(b+1,b+n+1);//离散

        cnt=unique(b+1,b+n+1)-b-1;//去重

        for(Re i=2;i<=m;++i){

            memset(C,0,sizeof(C));//每次都要清空，重新开始维护

            for(Re j=1;j<=n;++j)

                dp[i][j]=ask((k=lower_bound(b+1,b+cnt+1,a[j])-b)-1),add(k,dp[i-1][j]);

        }

        for(Re j=1;j<=n;++j)(ans+=dp[m][j])%=P;

        printf("Case #%d: %d\n",o,ans);

    }

}

3.【题目链接】

【简单题】

$The$ $Battle$ $of$ $Chibi$ $[UVA12983]$

【标签】动态规划/树状数组

【高档题】

方伯伯的玉米田 $[P3287]$

【标签】动态规划/二维树状数组
基站选址 $[P2605]$

【标签】动态规划/线段树

\[QAQ
\]

三：【决策单调性】

【前言】

形如 $dp[i]=min(dp[j]+w(j,i))$ $(L_i \leqslant j \leqslant R_i)$ 的 $dp$ 方程被称作 $1D/1D$ 动态规划，其中 $L_i$ 和 $R_i$ 单调递增，$w(j,i)$ 决定着优化策略选择。

针对决策点具有的特性，可以大大降低寻找最优决策点的时间。

其实质是优化 “决策”。

1.【定义】

【决策单调性】

设 $j_0[i]$ 表示 $dp[i]$ 转移的最优决策点，那么决策单调性可描述为 $\forall i \leqslant j,j_0[i] \leqslant j_0[j]$。也就是说随着 $i$ 的增大，所找到的最优决策点是递增态（非严格递增）。

【四边形不等式】

$w(x,y)$ 为定义在整数集合上的一个二元函数，若 $\forall a \leqslant b \leqslant c \leqslant d,w(a,c)+w(b,d) \leqslant w(a,d)+w(b,c)$，那么函数 $w$ 满足四边形不等式。

为什么叫做四边形不等式呢？在 $w(x,y)$ 函数的二维矩阵中挖一块四边形，左上角 加 右下角 小于等于 左下角 加 右上角。

2.【定理及其证明】

定理 (1)：四边形不等式的另一种定义

$w(x,y)$ 为定义在整数集合上的一个二元函数，若 $\forall a < b,w(a,b)+w(a+1,b+1) \leqslant w(a+1,b)+w(a,b+1)$，那么函数 $w$ 满足四边形不等式。

$证明：$

$\because \forall a < c,w(a,c)+w(a+1,c+1) \leqslant w(a+1,c)+w(a,c+1)$

$\therefore \forall a+1 < c,w(a+1,c)+w(a+2,c+1) \leqslant w(a+2,c)+w(a+1,c+1)$

$上下两式相加，有：$ $w(a,c)+w(a+2,c+1) \leqslant w(a,c+1)+w(a+2,c)$

$以此类推$ $\forall a \leqslant b\leqslant c,w(a,c)+w(b,c+1) \leqslant w(a,c+1)+w(b,c)$

$同理$ $\forall a \leqslant b \leqslant c \leqslant d,w(a,c)+w(b,d) \leqslant w(a,d)+w(b,c)$

定理 (2)：决策单调性

$1D/1D$ 动态规划具有决策单调性当且仅当函数 $w$ 满足四边形不等式 时成立。

$证明：$

$\because$ $j_0[i]$ $在$ $dp[i]$ $的决策点中最优$

$\therefore$ $\forall i \in [1,N],\forall j \in [0,j_0[i]-1],dp[j_0[i]]+w(j_0[i],i) \leqslant dp[j]+w(j,i)$

$易知$ $\forall i' \in [i+1,N]$，$均满足$ $j<j_0[i]<i<i'$。

$又$ $\because$ $函数$ $w$ $满足四边形不等式$

$\therefore$ $w(j,i)+w(j_0[i],i') \leqslant w(j,i')+w(j_0[i],i)$

$移项得：$ $w(j_0[i],i')-w(j_0[i],i) \leqslant w(j,i')-w(j,i)$

$与第一个式子相加，有：$ $dp[j_0[i]]+w(j_0[i],i') \leqslant dp[j]+w(j,i')$

最后的式子含义是：把 $j_0[i]$ 作为 $dp[i']$ 的决策点，一定比小于 $j_0[i]$ 的任意一个 $j$ 都要更好。也就是说，$dp[i’]$ 的最优决策点不可能小于 $j_0[i]$ ，即 $j_0[i'] \geqslant j_0[i]$，所以方程 $dp$ 具有决策单调性。

3.【证明决策单调性】

这里以玩具装箱 $toy$ $[P3195]$ 为例（因为这个比较好证 QAQ），先来证一波决策单调性。

设 $S[n]=\sum _{i=1}^n (C[i]+1)$，用 $dp[i]$ 表示装好前 $i$ 个的最小花费，则 $dp$ 方程为：$dp[i]=min(dp[j]+(S[i]-S[j]-1-L)^2)$。

很明显，这个方程是一个 $1D/1D$ 动态规划方程，其中 $w(i,j)=(S[i]-S[j]-1-L)^2$。

（注意在四边形不等式中的 $j$ 不是 $i$ 决策点，可以理解为 $i’$。而 $w(i,j)$ 的值可以理解为是由已完成的状态 $dp[i]$ 转移到 $dp[j]$ 所带有的附加价值）。

$证明：设$ $Q=S[i]-S[j]-1-L$

$\therefore w(i,j)=(S[i]-S[j]-1-L)^2=Q^2$

$\begin{equation*}
\begin{split}
\therefore w(i+1,j+1)=&(S[i+1]-S[j+1]-1-L)^2\\
=&((S[i]+C[i+1]+1)-(S[j]+C[j+1]+1)-1-L)^2\\
=&(Q+C[i+1]-C[j+1])^2
\end{split}
\end{equation*}$

$\begin{equation*}
\begin{split}
w(i,j+1)=&(S[i]-S[j+1]-1-L)^2\\
=&(S[i]-(S[j]+C[j+1]+1)-1-L)^2\\
=&(Q-C[j+1]-1)^2
\end{split}
\end{equation*}$

$\begin{equation*}
\begin{split}
w(i+1,j)=&(S[i+1]-S[j]-1-L)^2\\
=&((S[i]+C[i+1]+1)-S[j]-1-L)^2\\
=&(Q+C[i+1]+1)^2
\end{split}
\end{equation*}$

$\therefore w(i,j)+w(i+1,j+1)=2X^2+2C[i+1]X-2C[j+1]X+C[i+1]^2-2C[i+1]C[j+1]+C[j+1]^2$

$\therefore w(i+1,j)+w(i,j+1)=2X^2+2C[i+1]X-2C[j+1]X+C[i+1]^2+2C[i+1]+2C[j+1]+C[j+1]^2+2$

$\therefore w(i,j)+w(i+1,j+1)-w(i+1,j)+w(i,j+1)=-2(C[i+1]+1)(C[j+1]+1)$

$又 \because C[i],C[j] \geqslant 1$

$\therefore -2(C[i+1]+1)(C[j+1]+1) \leqslant -8$

$\therefore w(i,j)+w(i+1,j+1) \leqslant w(i+1,j)+w(i,j+1)$

由定理 $(1)$ 可知，函数 $w$ 满足四边形不等式。

又由定理 $(2)$可知，方程 $dp$ 具有决策单调性。

在实战中，通常使用打表的形式来验证 $w$ 函数的递变规律。

4.【实现方法】

关于决策单调性和斜率优化这两个东西的分类似乎有争议，有人说斜优是决策单调性的一种（好像就是二分栈来着？），也有人说斜优是针对斜率进行优化，是决策单调性是其一种方案（你谷某管理大大），我支持前一种说法。

（$ps.$ 对于此处及以下语言不严谨处，大家可以认真思考并给予建议，待日后对其理解加深后再行修改。）

这里选择不同的例题将二者分开讲。

【二分栈】

二分栈，顾名思义就是二分加栈。

用栈维护单调的决策点，二分找到最优决策点。

以 $Lightning$ $Conductor$ $[P3515]$ 为例，题目大意就是在给定长度为 $n$ 的序列 $a$ 中，对于每一个 $i$，找到最小的自然数 $p_i$ 满足对于任意的 $j \in [1,n]$，均有 $a_j \leqslant a_i+p_i-\sqrt{\left|i-j\right|}$ 。

把这个式子变下形：$p_i \geqslant a_j-a_i+\sqrt{\left|i-j\right|}$ 。

即 $p_i=max \{ a_j+\sqrt{\left|i-j\right|} \} -a_i$

即 $p_i = max \{ max\{a_j+\sqrt{i-j}\}(j \in [1,i]),max\{a_j+\sqrt{j-i}\}(j \in [i+1,n]) \}-a_i$

可以发现里面两个 $max$ 可以视为同一个问题（只要把序列翻转一下就可以了），所以只需要考虑求出对于每一个 $i$ 的 $max\{ a_j+\sqrt{i-j} \}$，其中 $j \in [1,i]$。

设 $y_j=a_j+\sqrt{i-j}$

那么我们会得到 $n$ 个关于 $i$ 函数，$p_i=max\{ y_j \}$。

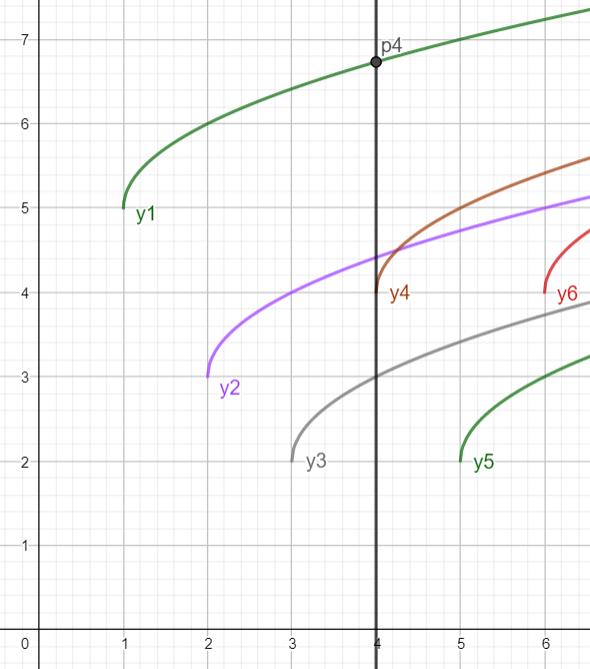
将样例画出来，如图：

可知当 $i=4$ 时，直线 $x=4$ 与 $y1=a_1+\sqrt{x-1}$ 的交点即为 $p_4$。

在上图中，对于任意 $j \in [1,n]$ ，$y1$ 总是在最上面，也就是说下面的其他函数可以踢掉不要，但由于 $sqrt$ 函数的增速递减，会出现如图中 $y2,y4$ 的情况，即存在一个交点使得在该点两边时两条直线的位置关系不同。此时如果没有上面的 $y1$，$y2,y4$ 都有可能成为答案，所以不能乱踢。

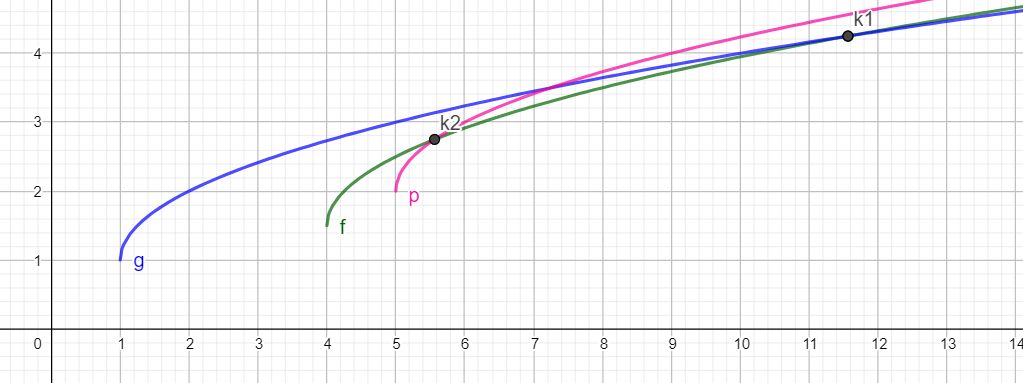
看下面这种情况：

设 $k_1$ 为 $y_1,y_2$ 的交点，$k_2$ 为 $y_2,y_3$ 的交点。

此时 $k_1 > k_2$，可以发现 $y_2$ 始终在其他直线的下面，可以放心的将其踢掉。

所以维护出来的决策集合大概就是酱紫的：

对于不同的 $i$ 来说，都有一个互不不同的直线在最上方，所以该决策集合里的直线都是有用的。可以从图中看出，最优决策点单调递增（决策单调性的数学证明较麻烦，本人能力不足，不作探讨）。

维护决策集合用单调队列，查找直线交点用二分，随便搞搞就行了。

时间复杂度为 $O(nlogn)$。

【分治】

为方便描述，用 $dp[a,b]$ 表示 $dp[a],dp[a+1],dp[a+2]...dp[b]$。

假设我们已知 $dp[l,r]$ 的最优决策点均位于 $[L,R]$，再设 $dp[mid]$ 的最优决策点为 $j_0$，其中 $mid=(l+r)/2$。根据决策单调性的定义可知：

$dp[l,mid-1]$ 的最优决策点位于 $[L,k]$，

$dp[mid+1,r]$ 的最优决策点位于 $[k,R]$。

原问题变成了两个规模更小的同类型问题，所以可以用分治来对 $dp$ 进行优化。

分治的话理解和代码都要简单一些，但在某些情况下可能要被卡，时间复杂度会严重退化，所以还是二分栈的实用性更高。

还是以 $Lightning$ $Conductor$ $[P3515]$ 为例，每次的分治中先暴力扫一遍找到 $p[mid=(l+r)/2]$ 的最优决策点 $j_0$，然后做一下左边，再做一下右边，然后 $...$ 然后 $...$ 就没了。

时间复杂度为 $O(nlogn)$。

5.【Code】

二分栈

#include<algorithm>

#include<cstdio>

#include<cmath>

#define Re register int

using namespace std;

const int N=5e5+3;

int i,j,n,h,t,a[N],Q[N],Poi[N];

double p[N],sqr[N];

inline void in(Re &x){

    int f=0;x=0;char c=getchar();

    while(c<'0'||c>'9')f|=c=='-',c=getchar();

    while(c>='0'&&c<='9')x=(x<<1)+(x<<3)+(c^48),c=getchar();

    x=f?-x:x;

}

inline double Y(Re i,Re j){return a[j]+sqr[i-j];}

inline int find_Poi(int j1,int j2){//找到两个直线的交点i

    Re l=j2,r=n,mid,ans=n+1;//为了处理两个直线没有交点的情况，用一个变量记录答案

    while(l<=r){

        mid=l+r>>1;

        if(Y(mid,j1)<=Y(mid,j2))ans=mid,r=mid-1;

//当前这个位置i使得直线j1的纵坐标小于直线j2的纵坐标，说明这个点i在交点的右方，所以右边界要缩小

        else l=mid+1;

    }

    return ans;

}

inline void sakura(){

    h=1,t=0;

    for(i=1;i<=n;++i){//由于i本身也是一个决策点，所以要先入队再取答案择优

    	while(h<t&&Poi[t-1]>=find_Poi(Q[t],i))--t;//如果出现了上述可踢的情况，出队

    	Poi[t]=find_Poi(Q[t],i),Q[++t]=i;

    	while(h<t&&Poi[h]<=i)++h;

//找到第一个位置j使得直线Q[j]与直线Q[j+1]的交点大于i，

//那么直线Q[j]就是i前面在最上面的直线，即答案，自己画个图模拟一下就懂了

    	p[i]=max(p[i],Y(i,Q[h]));

    }

}

int main(){

    in(n);

    for(Re i=1;i<=n;++i)in(a[i]),sqr[i]=sqrt(i);

    sakura();

    for(Re i=1;i<n-i+1;++i)swap(a[i],a[n-i+1]),swap(p[i],p[n-i+1]);

    sakura();

    for(Re i=n;i;--i)printf("%d\n",(int)ceil(p[i])-a[i]);

}

分治

#include<algorithm>

#include<cstdio>

#include<cmath>

#define Re register int

using namespace std;

const int N=5e5+3;

int i,j,n,h,t,a[N],Q[N],Poi[N];

double tmp,p[N],sqr[N];

inline void in(Re &x){

    int f=0;x=0;char c=getchar();

    while(c<'0'||c>'9')f|=c=='-',c=getchar();

    while(c>='0'&&c<='9')x=(x<<1)+(x<<3)+(c^48),c=getchar();

    x=f?-x:x;

}

inline void sakura(Re l,Re r,Re L,Re R){

    if(l>r)return;

    Re mid=l+r>>1,j0;double mx=0;

    for(Re j=L;j<=mid&&j<=R;++j)

    //暴力找p[i]的最优决策点j0，而其决策点j必须满足j<=i，即此处的j<=mid

    	if((tmp=a[j]+sqr[mid-j])>mx)mx=tmp,j0=j;

    p[mid]=max(p[mid],mx);

    sakura(l,mid-1,L,j0),sakura(mid+1,r,j0,R);

}

int main(){

    in(n);

    for(Re i=1;i<=n;++i)in(a[i]),sqr[i]=sqrt(i);

    sakura(1,n,1,n);

    for(Re i=1;i<n-i+1;++i)swap(a[i],a[n-i+1]),swap(p[i],p[n-i+1]);

    sakura(1,n,1,n);

    for(Re i=n;i;--i)printf("%d\n",(int)ceil(p[i])-a[i]);

}

6.【题目链接】

【中档题】

$Lightning$ $Conductor$ $[P3515]$

【标签】动态规划/决策单调性
$Noi$ 嘉年华 $[P1973]$

【标签】动态规划/决策单调性
大佬 $[P3724]$

【标签】动态规划/决策单调性

【高档题】

诗人小 $G$ $[P1912]$

【标签】动态规划/单调队列/贪心

\[QAQ
\]

四：【单调队列优化 DP】

【前言】

形如 $dp[i]=max/min \{ dp[j]+funtion(i)+function(j) \}$ 的 $dp$ 方程均可尝试使用单调队列优化。

单调栈和单调队列给我们展现出了一种思想：在保证正确性的前提下，及时排除不可能的决策点，保持决策集合内部的有序性和查找决策的高效性。之前的二分栈，此处的单调队列优化，和后面的斜率优化都是以此为核心来运作的。

其实质是优化 “决策”。

1.【单调队列的简单运用】

【T1】

琪露诺 $[P1725]$（盗版滑动窗口QAQ）。

【题目大意】

在给定序列中找出一条路径使其经过的点之和最大，且每次可走的距离在给定区间 $[l,r]$ 以内。

【分析】

方程非常简单：$dp[i]=max\{ dp[j]+a[i] \} (i-r \leqslant j \leqslant i-l)$ 。

在某一次决策中，由于决策点 $j$ 只可能在 $[i-l,i-r]$ 这一段区间内，可以只将这些点放入决策集合。

而 $l,r$ 是定值，当 $i$ 不断增大时，之前小于 $i-l$ 的 $j$ 现在还是小于 $i-l$，所以可以永远地踢掉。

若 $j < j'$ 且 $dp[j] \leqslant dp[j']$，那么 $dp[j]$ 也可以永远地踢掉。为什么呢？ $j$ 在 $j'$ 的前面，一定会先成为不合法决策点，而 $j$ 的价值又比 $j'$ 小，因此留下来只是浪费扫描的时间。

最终维护出了一个价值递减的单调队列。

【Code】

#include<algorithm>

#include<cstring>

#include<cstdio>

#define Re register int

using std::max;

const int N=2e5+3;

int n,l,r,h=1,t,a[N],Q[N];

long long ans=-2e9,dp[N];

inline void in(Re &x){

    int f=0;x=0;char c=getchar();

    while(c<'0'||c>'9')f|=c=='-',c=getchar();

    while(c>='0'&&c<='9')x=(x<<1)+(x<<3)+(c^48),c=getchar();

    x=f?-x:x;

}

int main(){

    in(n),in(l),in(r);

    memset(dp,-127,sizeof(dp));

    Q[++t]=0;

    for(Re i=0;i<=n;++i)in(a[i]);

    dp[0]=a[0];

    for(Re i=l;i<=n;i++){//注意枚举起点是l不是1

    	while(h<=t&&dp[Q[t]]<=dp[i-l])--t;//维护单调递减

    	Q[++t]=i-l;//入队

    	while(h<=t&&Q[h]<i-r)++h;//保证决策点合法

    	dp[i]=dp[Q[h]]+a[i];//取出最优决策点

    	if(i>=n-r)ans=max(ans,dp[i]);

    }

    printf("%lld",ans);

}

【T2】

$fence$ $[POJ1821]$

【题目大意】

$M$ 个工人要对 $N$ 块木板进行粉刷。工人 $i$ 要么不刷，要么就刷不超过 $L_i$ 块并且包含 $S_i$ 的连续一段木板，每粉刷一块木板有 $P_i$ 的报酬。要求使总报酬最大。

【分析】

$S_i$ 的散乱分布非常讨厌，所以先把工人按 $S_i$ 排个序。

主要信息有“工人序号”，“木板序号”，“报酬”这三个，而其中“报酬”为所求答案，可以用 $dp[i][j]$ 表示前 $i$ 个工人刷完前 $j$ 块木板所得总报酬。

考虑状态转移：

第 $i$ 个工人可以跳过不刷木板，也可以跳过第 $j$ 块木板不刷，因此先在 $dp[i-1][j]$ 和 $dp[i][j-1]$ 当中取个最大值。

工人 $i$ 想要粉刷的区间 $[k+1,j]$ 必须包括 $S_i$，并且区间长度要小于等于 $L_i$。

所以得出 $dp$ 转移方程：$dp[i][j]=max \{ dp[i-1][j],dp[i][j-1],dp[i-1][k]+P_i*(j-k) \}$，其中 $S_i \leqslant j$ 且 $k \in [j-L_i,S_i-1]$。

$k$ 为决策点，$P_i*j$ 为定值可以单独提出来，所以实际上就是上面琪露诺 $[P1725]$一样的类型，只是加了一维而已。

最终维护出了一个 $dp[i-1][k]-P_i*k$ 递减的单调队列。

【Code】

#include<algorithm>

#include<cstring>

#include<cstdio>

#define Re register int

using namespace std;

const int N=16005;

struct QAQ{int L,P,S;}a[105];

int n,m,i,j,k,Q[N],W[N],dp[105][N];

inline bool cmp(QAQ a,QAQ b){return a.S<b.S;}

int main(){

    while(scanf("%d%d",&n,&m)!=EOF){

    	memset(dp,0,sizeof(dp));

    	memset(a,0,sizeof(a));

    	for(i=1;i<=m;++i)scanf("%d%d%d",&a[i].L,&a[i].P,&a[i].S);

    	std::sort(a+1,a+m+1,cmp);

    	for(i=1;i<=m;++i){

            Re l=1,r=0,tmp,Si=a[i].S,Li=a[i].L,Pi=a[i].P;

            for(k=max(0,Si-Li);k<Si;++k){

            //k+1为工人i开始刷的位置，max(1,Si-Li+1)<=k+1<=Si

            	tmp=dp[i-1][k]-Pi*k;

            	while(l<=r&&Q[r]<=tmp)--r;

            	Q[++r]=tmp,W[r]=k;

            }

            for(j=1;j<=n;++j){

            	dp[i][j]=max(dp[i-1][j],dp[i][j-1]);

                if(Si+Li>j&&j>=Si){//Si+Li-1>=j>=Si

                    while(l<=r&&W[l]+Li<j)++l;//W[r]+1+Li-1<j

                    if(l<=r)dp[i][j]=max(dp[i][j],Q[l]+Pi*j);

                }

            }

    	}

    	printf("%d\n",dp[m][n]);

    }

}

2.【单调队列优化多重背包】

先来回顾一下多重背包问题。

用 $v,w,c$ 分别表示物品重量，价值，数量，$n$ 为物品数量，$V$ 为背包容量。$dp$ 方程为：$dp[j]=max\{ dp[j-k*v[i]]+k*w[i] \}$ $(j \in [v[i],V],$ $k \in [1,min(c[i],j/v[i])])$

还可以用二进制拆分来进行优化，但就是有这样一道题，连 $log$ 都要卡：多重背包 $[CodeVS5429]$。所以还需要考虑更高效的算法。

但说来说去似乎都和单调队列扯不上关系。

为何？

观察 $dp[j]$ 和 $dp[j-1]$ 决策集合：

$dp[j]: \{ j \% v[i]...j-2*v[i],j-v[i] \}$

$dp[j-1]: \{ (j-1) \% v[i]...(j-1)-2*v[i],(j-1)-v[i] \}$

$dp[j]$ 的每一个决策点都与 $dp[j-1]$ 不同，很难根据 $dp[j-1]$ 的决策集合转移成 $dp[j]$ 的决策集合。

再看 $dp[j]$ 和 $dp[j-v[i]]$：

$dp[j]: \{ j-c[i]*v[i]...j-2v[i],j-v[i] \}$

$dp[j-v[i]]: \{ j-(c[i]+1)*v[i]...j-3v[i],j-2v[i] \}$

可以发现上面只是比下面的区别仅仅在于 $j-(c[i]+1)*v[i]$ 和 $j-v[i]$ ，恰好满足单调队列的一个特性：但有新的决策出现时，决策点集合中会去掉一部分不合法的，再加上一部分新来的。

所以我们可以按照 $j%v[i]$ 的余数来分一下：

$dp[j](j\%v[i]=0):\{0,v[i],2v[i]...j-2v[i],j-v[i]\}$

$dp[j](j\%v[i]=1):\{1,v[i]+1,2v[i]+1...j-2v[i],j-v[i] \}$

$...$

$dp[j](j\%v[i]=v[i]-1):\{v[i]-1,2v[i]-1...j-2v[i],j-v[i]\}$

设 $j=p*v[i]+r$，那么原方程可改为： $dp[p*v[i]+r]=max\{ dp[r+k*v[i]]+(p-k)*w[i] \}$ $(r \in [0,v[i]-1],$ $p \in [1,\lfloor(V-r)/v[i]\rfloor],$ $k \in [p-min( \lfloor V/w[i]\rfloor ,c[i]),p])$

只要在最外层将 $i,r,p$ 都枚举出来，这就是一个标准的单调队列可优化方程，用类似 $fence$ $[POJ1821]$ 的方法维护即可。

时间复杂度为 $O(N*V)$ 。

【Code】

#include<cstdio>

#define Re register int

const int N=7003,M=7003;

int n,h,t,V,mp,tmp,v[N],w[N],c[N],Q[N],K[N],dp[M];

inline void in(Re &x){

    Re fu=0;x=0;char ch=getchar();

    while(ch<'0'||ch>'9')fu|=ch=='-',ch=getchar();

    while(ch>='0'&&ch<='9')x=(x<<1)+(x<<3)+(ch^48),ch=getchar();

    x=fu?-x:x;

}

inline int max(Re a,Re b){return a>b?a:b;}

inline int min(Re a,Re b){return a<b?a:b;}

int main(){

    in(n),in(V);

    for(Re i=1;i<=n;++i)in(v[i]),in(w[i]),in(c[i]);

    for(Re i=1;i<=n;++i)

    	for(Re r=0;r<v[i];++r){

            h=1,t=0,mp=(V-r)/v[i];

            for(Re p=0;p<=mp;++p){

            	tmp=dp[p*v[i]+r]-w[i]*p;

            	while(h<=t&&Q[t]<=tmp)--t;

            	Q[++t]=tmp,K[t]=p;

            	while(h<=t&&p-K[h]>min(c[i],V/v[i]))++h;

            	dp[p*v[i]+r]=max(dp[p*v[i]+r],Q[h]+p*w[i]);

            }

        }

    printf("%d",dp[V]);

}

3.【题目链接】

【简单题】

琪露诺 $[P1725]$

【标签】动态规划/单调队列

【中档题】

$fence$ $[POJ1821]$

【标签】动态规划/单调队列
多重背包 $[CodeVS5429]$

【标签】动态规划/单调队列/多重背包
我要长高 $[UESTC594]$

【标签】动态规划/单调队列

\[QAQ
\]

五：【斜率优化 DP】

由于篇幅过大，已搬出。。。。。

【学习笔记】动态规划—斜率优化DP（超详细）

补充：其实质是优化 “决策”。

\[QAQ
\]

【参考文献】

（本文部分内容摘自以下文章）