红黑树原理详解及golang实现
红黑树原理详解及golang实现
在看红黑树原理之前，先看下二叉查找树。
二叉查找树
二叉查找树，又称二叉排序树，二叉搜索树。
性质
它具备以下性质：
1、左子树上的所有节点均小于它的根节点值。
2、右子树上的所有节点的值均大于它根节点的值。
3、左右子树也分别为二叉排序树。
4、没有键值相等的节点。
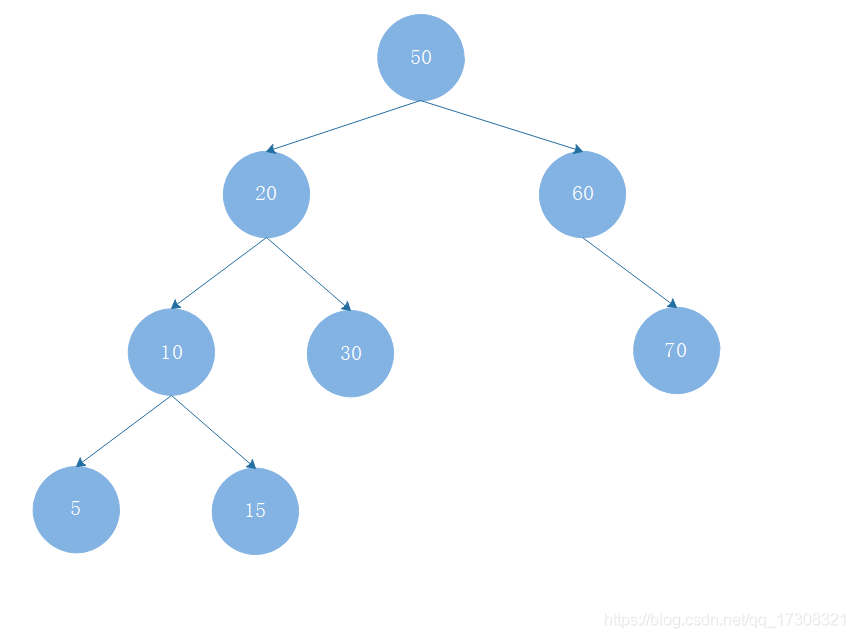
既然叫搜索树，那这种结构的好处当然也就是搜索咯，
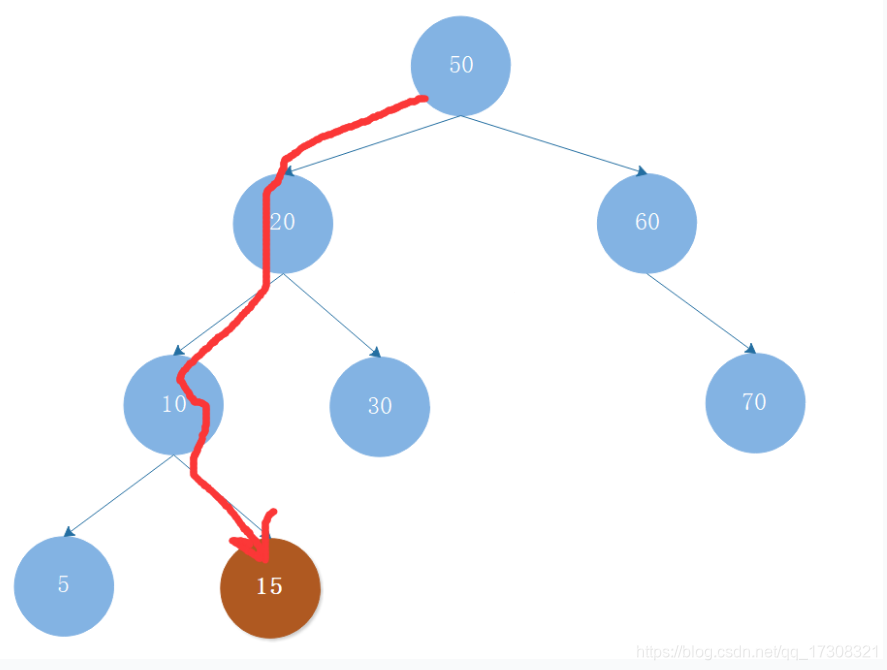
假如我们要查找15
1、从root节点开始，15<50，找左子树。
2、15<20，找左子树，
3、15>10，找右子树，这样便找到15了。
插入也是类似方法，一层一层比较大小，找到合适的位置插入。
时间复杂度
看见它查找的次数等同于树的高度，在最好的情况下，其平均查找次数和log 2 (n)成正比。
当然也有坏情况，当先后插入的关键字有序时，构成的二叉排序树蜕变为单支树，树的深度和其节点数成正比(和顺序查找相同）.
例如依序插入 ： 100、200、90、80、70、60、50、40
就会成为如下图形态：
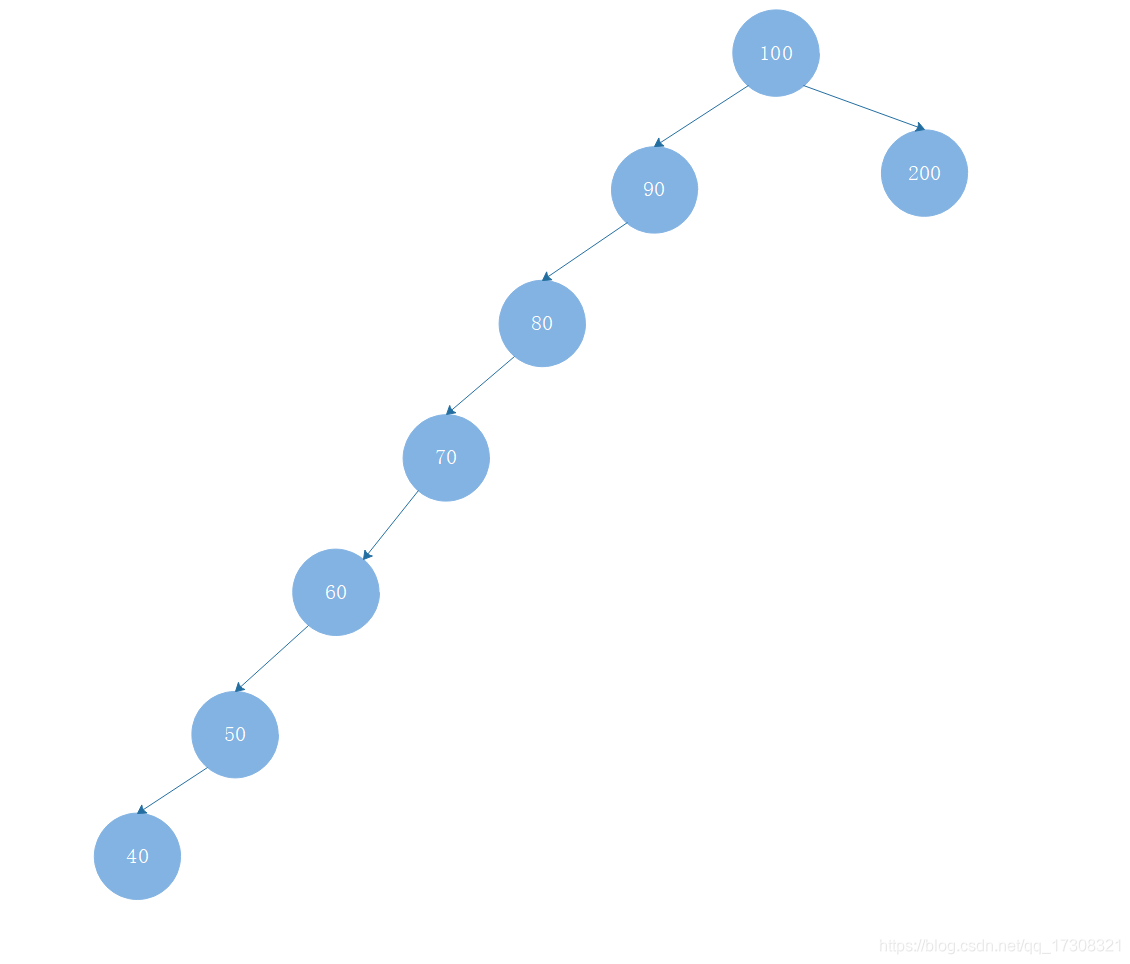
为了解决这种不平衡的情形，就有了红黑树。
红黑树
性质
红黑树是一种自平衡的二叉搜索树，它包含了二叉搜索树的特性，同时具备以下性质：
1、所有节点的颜色不是红色就是黑色。
2、根节点是黑色。
3、每个叶子节点都是黑色的空节点(nil)。
4、每个红色节点的两个子节点都是黑色。(从每个叶子到根节点的所有路径上不能有两个连续的红色节点)
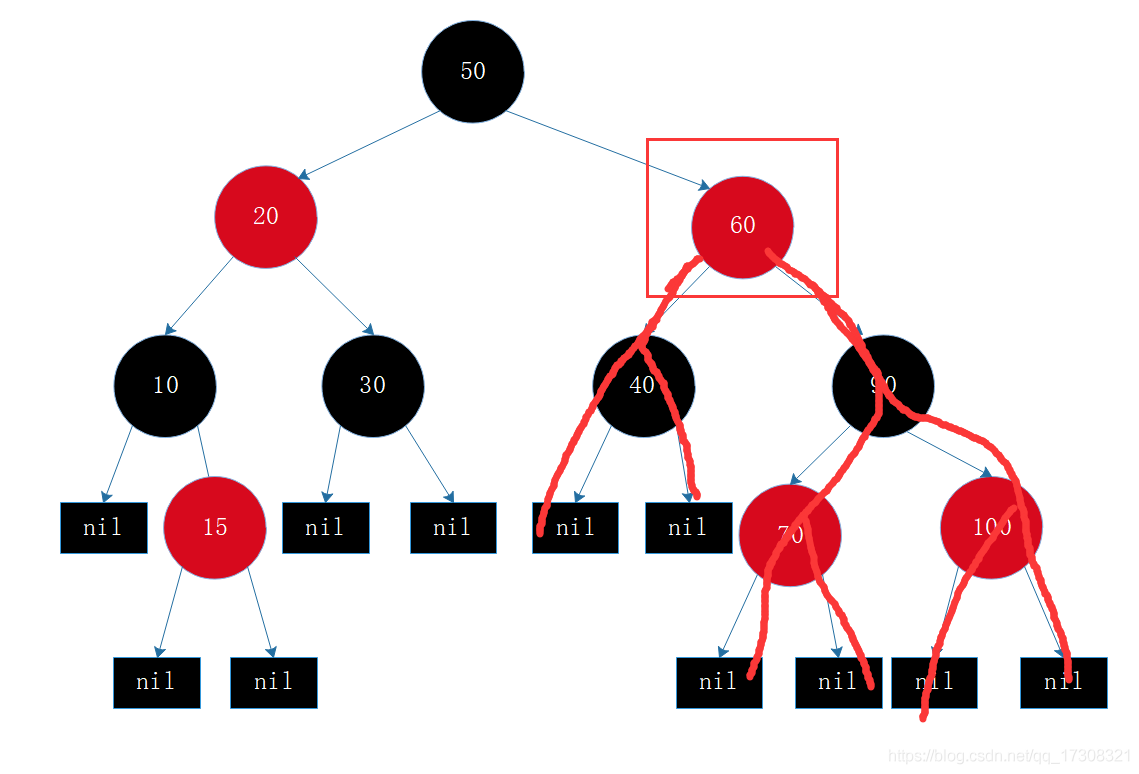
5、从任一节点到其叶子节点的所有路径上都包含相同数目的黑节点。
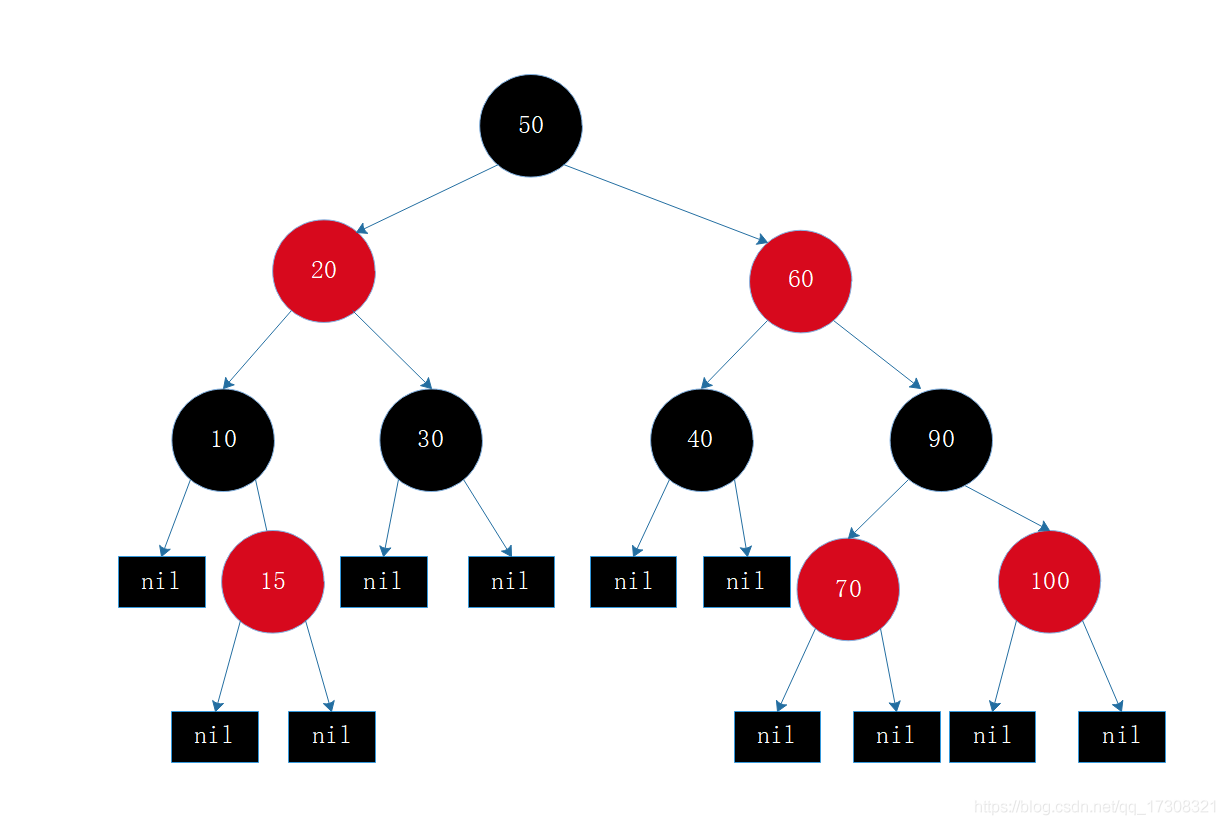
前四都能理解其意思吧，所以只解释下第五点，比如60这个节点，到其所有叶子节点的路径都只包含1个黑色节点：40和90。
operation
红黑树为了维持它的这5点性质，于是它支持了这么几个操作 ，
变色 ： 顾名思义变色，红变黑，黑变红。
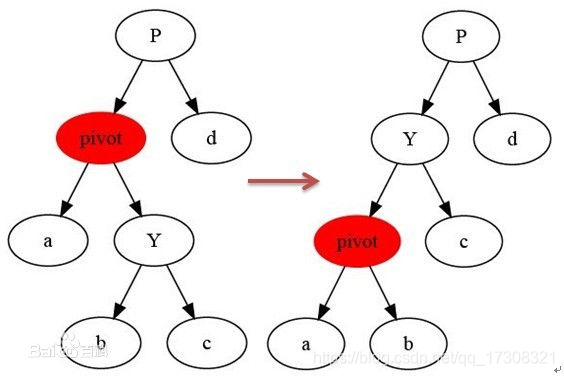
左旋转 : 这里借用百度百科两张旋转图，以图中红色节点为中心，中心节点为右孩子替代，而自己成为它的左孩子，同时节点b作为pivot的有孩子(至于为什么是右孩子，b原本就在pivot的右子树上，所以肯定大于pivot)。
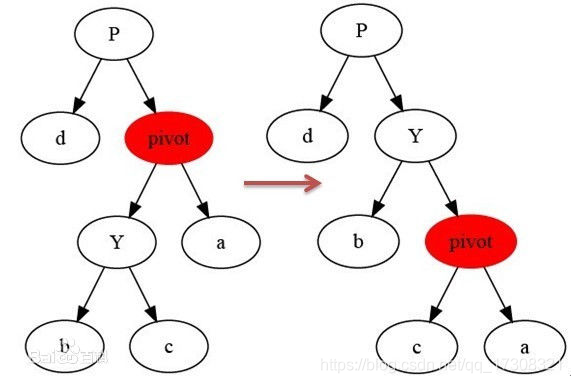
右选装 : 同左旋转，中心点顺时钟旋转，成为其原来左孩子的右孩子，原来左孩子的右孩子则成为原中心点的左孩子。
接着看看红黑树的插入，看看它是如何通过这几个op维持红黑树这5个性质的。
红黑树的插入
关于插入的特点 ： 由于性质5的约束，每次插入的节点颜色必然为红色。
插入的化存在几种情形，复杂的树可能会涉及到循环的向树上检索做自平衡，这里先从一颗空树开始先简单理解下这些情形。
情形1：空树
直接插入，直接作为根节点，同时由于性质1的约束，通过变色op变为黑色即可。
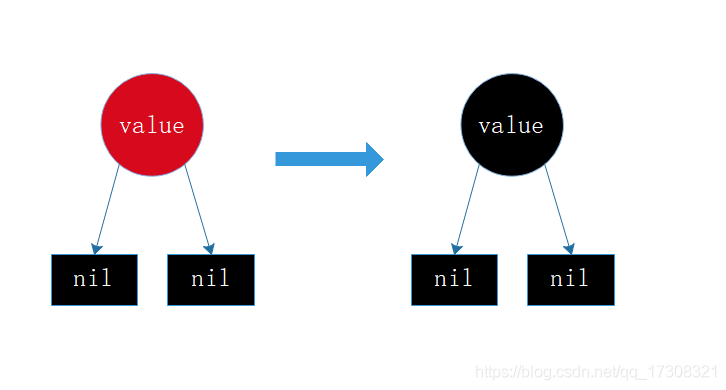
情形2：插入节点父节为黑色，
不违反任何性质，无需做任何修改。
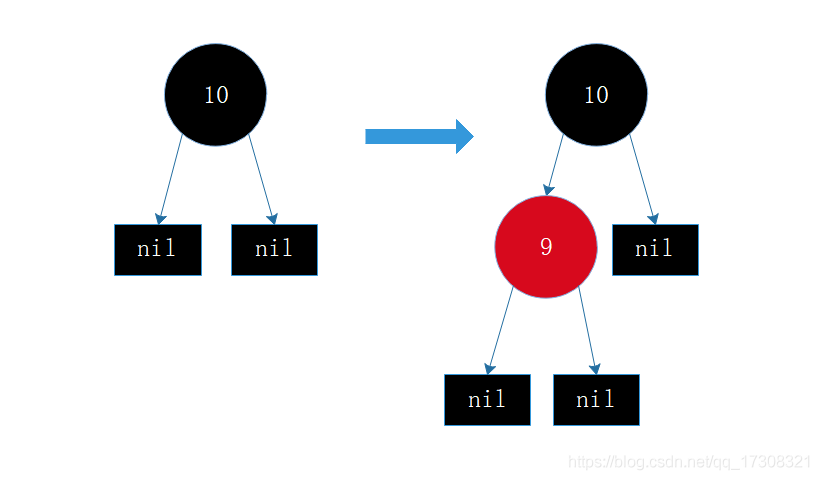
情形3 插入节点的父节点为红色，父节点为父父节点的左孩子，父父节点的右孩子为黑色，插入节点为左孩子(或者父节点为父父节点的右孩子，父父节点的左孩子为黑色，插入节点为右孩子)。
这是一种插入节点和父节点在一个方向上的情况(例如父节点为左孩子，插入节点也为左孩子)和情形5相反
父节点 及 父父节点变色，再进行左/右旋转， 具体左还是右看你插入的节点的父节点是左子树还是右子树，图例为左子树。
此处 : 变色 - > 右旋转
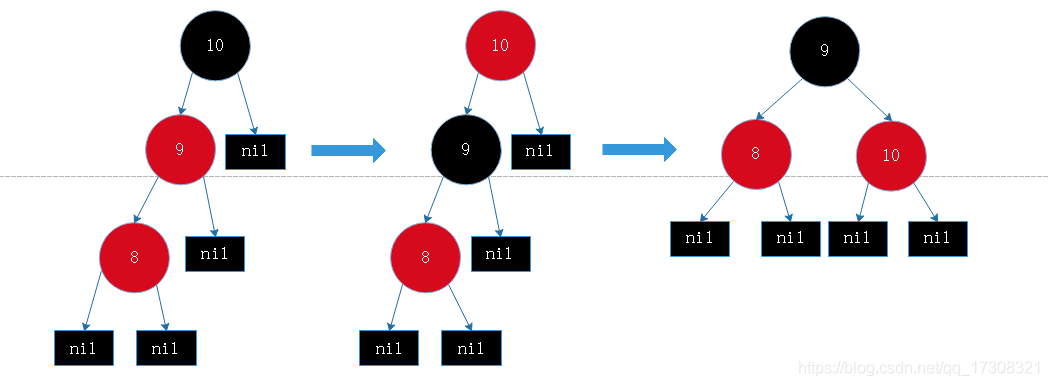
情形4 插入节点父节点为红色，父父节点的左/右孩子为红色
先将父节点和父父节点右孩子变黑，父父节点变红，然后将父节点当做新插入的红色节点一样递归向上进行平衡红黑树性质操作。 若父节点为根节点直接变父节点为黑色即可.
此处 : 变色 -> 变色
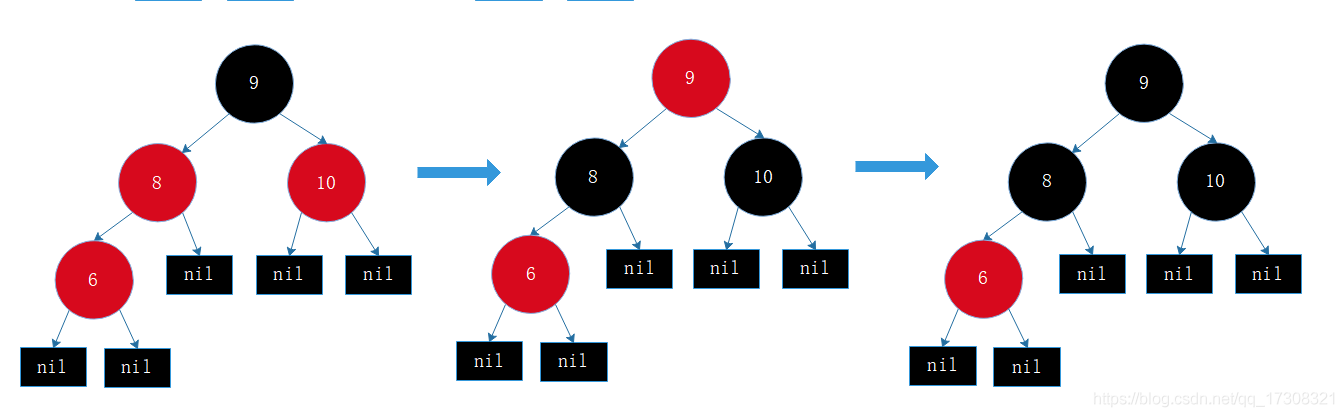
情形5 插入节点的父节点为红色，父节点为父父节点的左孩子，父父节点的右孩子为黑色，插入节点为右孩子(或者父节点为父父节点的右孩子，父父节点的左孩子为黑色，插入节点为左孩子)。
和情形3类比是一种反向情况，这种情况进行两次旋转，
先左/右旋转，旋转后变成了情形3，接着按情形3变换即可。
此处 ：左旋转 -> 变色 -> 右旋转
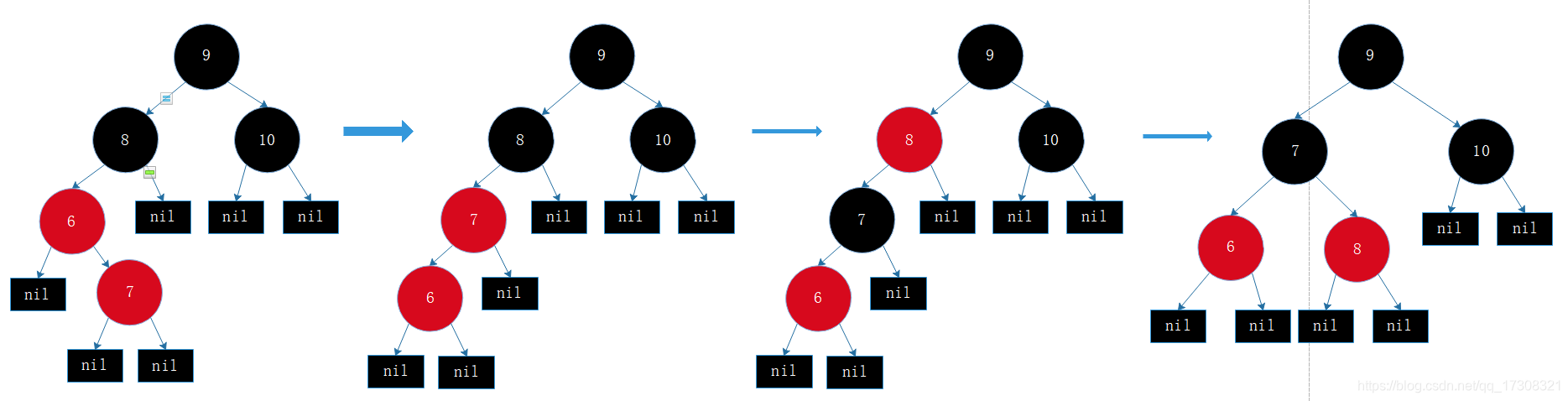
golang实现
类型定义
需要注意的是 红黑树的NIL节点需要单独定义出来，不能直接用nil哦。
const (
RED = true
BLACK = false
)
type Node struct {
Parent *Node
Left *Node
Right *Node
color bool
Item
}
type Rbtree struct {
NIL *Node
root *Node
count uint64
}
func New() *Rbtree{
node := Node{nil, nil, nil, BLACK, nil}
return &Rbtree{
NIL : &node,
root : &node,
count : 0,
}
}
leftRotate
// Left Rotate
func (rbt *Rbtree) LeftRotate(no *Node) {
// Since we are doing the left rotation, the right child should *NOT* nil.
if no.Right == nil {
return
}
// | |
// X Y
// / \ left rotate / \
// α Y -------------> X γ
// / \ / \
// β γ α β
rchild := no.Right
no.Right = rchild.Left
if rchild.Left != nil {
rchild.Left.Parent = no
}
rchild.Parent = no.Parent
if no.Parent == nil {
rbt.root = rchild
} else if no == no.Parent.Left {
no.Parent.Left = rchild
} else {
no.Parent.Right = rchild
}
rchild.Left = no
no.Parent = rchild
}
func LeftRotateTest(){
var i10 Int = 10
var i12 Int = 12
rbtree := New()
x := &Node{rbtree.NIL, rbtree.NIL, rbtree.NIL, BLACK, i10}
rbtree.root = x
y := &Node{rbtree.root.Right, rbtree.NIL, rbtree.NIL, RED, i12}
rbtree.root.Right = y
log.Println("root : ", rbtree.root)
log.Println("left : ", rbtree.root.Left)
log.Println("right : ", rbtree.root.Right)
rbtree.LeftRotate(rbtree.root)
log.Println("root : ", rbtree.root)
log.Println("left : ", rbtree.root.Left)
log.Println("right : ", rbtree.root.Right)
}
RightRotate
// Right Rotate
func (rbt *Rbtree) RightRotate(no *Node) {
if no.Left == nil {
return
}
// | |
// X Y
// / \ right rotate / \
// Y γ -------------> α X
// / \ / \
// α β β γ
lchild := no.Left
no.Left = lchild.Right
if lchild.Right != nil {
lchild.Right.Parent = no
}
lchild.Parent = no.Parent
if no.Parent == nil {
rbt.root = lchild
} else if no == no.Parent.Left {
no.Parent.Left = lchild
} else {
no.Parent.Right = lchild
}
lchild.Right = no
no.Parent = lchild
}
func RightRotateTest(){
var i10 Int = 10
var i12 Int = 12
rbtree := New()
x := &Node{rbtree.NIL, rbtree.NIL, rbtree.NIL, BLACK, i10}
rbtree.root = x
y := &Node{rbtree.root.Right, rbtree.NIL, rbtree.NIL, RED, i12}
rbtree.root.Right = y
log.Println("root : ", rbtree.root)
log.Println("left : ", rbtree.root.Left)
log.Println("right : ", rbtree.root.Right)
rbtree.RightRotate(rbtree.root)
log.Println("root : ", rbtree.root)
log.Println("left : ", rbtree.root.Left)
log.Println("right : ", rbtree.root.Right)
}
Item Interface
值类型接口
type Item interface {
Less(than Item) bool
}
type Int int
func (x Int) Less(than Item) bool {
log.Println(x, " ", than.(Int))
return x < than.(Int)
}
type Uint32 uint32
func (x Uint32) Less(than Item) bool {
log.Println(x, " ", than.(Uint32))
return x < than.(Uint32)
}
type String string
func (x String) Less(than Item) bool {
log.Println(x, " ", than.(String))
return x < than.(String)
}
func ItemTest(){
var itype1 Int = 10
var itype2 Int = 12
log.Println(itype1.Less(itype2))
var strtype1 String = "sola"
var strtype2 String = "ailumiyana"
log.Println(strtype1.Less(strtype2))
}
insert
func (rbt *Rbtree) Insert(no *Node) {
x := rbt.root
var y *Node = rbt.NIL
for x != rbt.NIL {
y = x
if less(no.Item, x.Item) {
x = x.Left
} else if less(x.Item, no.Item) {
x = x.Right
} else {
log.Println("that node already exist")
}
}
no.Parent = y
if y == rbt.NIL {
rbt.root = no
} else if less(no.Item, y.Item) {
y.Left = no
} else {
y.Right = no
}
rbt.count++
rbt.insertFixup(no)
}
func (rbt *Rbtree) insertFixup(no *Node) {
for no.Parent.color == RED {
if no.Parent == no.Parent.Parent.Left {
y := no.Parent.Parent.Right
if y.color == RED {
//
// 情形 4
log.Println("TRACE Do Case 4 :", no.Item)
no.Parent.color = BLACK
y.color = BLACK
no.Parent.Parent.color = RED
no = no.Parent.Parent //循环向上自平衡.
} else {
if no == no.Parent.Right {
//
// 情形 5 : 反向情形
// 直接左旋转 , 然后进行情形3(变色->右旋)
log.Println("TRACE Do Case 5 :", no.Item)
if no == no.Parent.Right {
no = no.Parent
rbt.LeftRotate(no)
}
}
log.Println("TRACE Do Case 6 :", no.Item)
no.Parent.color = BLACK
no.Parent.Parent.color = RED
rbt.RightRotate(no.Parent.Parent)
}
} else { //为父父节点右孩子情形，和左孩子一样，改下转向而已.
y := no.Parent.Parent.Left
if y.color == RED {
no.Parent.color = BLACK
y.color = BLACK
no.Parent.Parent.color = RED
no = no.Parent.Parent
} else {
if no == no.Parent.Left {
no = no.Parent
rbt.RightRotate(no)
}
no.Parent.color = BLACK
no.Parent.Parent.color = RED
rbt.LeftRotate(no.Parent.Parent)
}
}
}
rbt.root.color = BLACK
}
func InsertTest(){
rbtree := New()
rbtree.Insert(&Node{rbtree.NIL, rbtree.NIL, rbtree.NIL, RED, Int(10)})
rbtree.Insert(&Node{rbtree.NIL, rbtree.NIL, rbtree.NIL, RED, Int(9)})
rbtree.Insert(&Node{rbtree.NIL, rbtree.NIL, rbtree.NIL, RED, Int(8)})
rbtree.Insert(&Node{rbtree.NIL, rbtree.NIL, rbtree.NIL, RED, Int(6)})
rbtree.Insert(&Node{rbtree.NIL, rbtree.NIL, rbtree.NIL, RED, Int(7)})
log.Println("rbtree counts : ", rbtree.count)
log.Println("------ ", rbtree.root.Item)
log.Println("----", rbtree.root.Left.Item, "---", rbtree.root.Right.Item)
log.Println("--", rbtree.root.Left.Left.Item, "-", rbtree.root.Left.Right.Item)
}
InsertTest() 仔细瞧瞧这就是我们 讲情形那棵树 哈 。
完整代码
package main
import(
"log"
)
const (
RED = true
BLACK = false
)
//-----------------------------------
//Item interface
//
type Item interface {
Less(than Item) bool
}
type Int int
func (x Int) Less(than Item) bool {
log.Println(x, " ", than.(Int))
return x < than.(Int)
}
type Uint32 uint32
func (x Uint32) Less(than Item) bool {
log.Println(x, " ", than.(Uint32))
return x < than.(Uint32)
}
type String string
func (x String) Less(than Item) bool {
log.Println(x, " ", than.(String))
return x < than.(String)
}
//-----------------------------------
type Node struct {
Parent *Node
Left *Node
Right *Node
color bool
Item
}
type Rbtree struct {
NIL *Node
root *Node
count uint64
}
func New() *Rbtree{
node := &Node{nil, nil, nil, BLACK, nil}
return &Rbtree{
NIL : node,
root : node,
count : 0,
}
}
func less(x, y Item) bool {
return x.Less(y)
}
// Left Rotate
func (rbt *Rbtree) LeftRotate(no *Node) {
// Since we are doing the left rotation, the right child should *NOT* nil.
if no.Right == rbt.NIL {
return
}
// | |
// X Y
// / \ left rotate / \
// α Y -------------> X γ
// / \ / \
// β γ α β
rchild := no.Right
no.Right = rchild.Left
if rchild.Left != rbt.NIL {
rchild.Left.Parent = no
}
rchild.Parent = no.Parent
if no.Parent == rbt.NIL {
rbt.root = rchild
} else if no == no.Parent.Left {
no.Parent.Left = rchild
} else {
no.Parent.Right = rchild
}
rchild.Left = no
no.Parent = rchild
}
// Right Rotate
func (rbt *Rbtree) RightRotate(no *Node) {
if no.Left == rbt.NIL {
return
}
// | |
// X Y
// / \ right rotate / \
// Y γ -------------> α X
// / \ / \
// α β β γ
lchild := no.Left
no.Left = lchild.Right
if lchild.Right != rbt.NIL {
lchild.Right.Parent = no
}
lchild.Parent = no.Parent
if no.Parent == rbt.NIL {
rbt.root = lchild
} else if no == no.Parent.Left {
no.Parent.Left = lchild
} else {
no.Parent.Right = lchild
}
lchild.Right = no
no.Parent = lchild
}
func (rbt *Rbtree) Insert(no *Node) {
x := rbt.root
var y *Node = rbt.NIL
for x != rbt.NIL {
y = x
if less(no.Item, x.Item) {
x = x.Left
} else if less(x.Item, no.Item) {
x = x.Right
} else {
log.Println("that node already exist")
}
}
no.Parent = y
if y == rbt.NIL {
rbt.root = no
} else if less(no.Item, y.Item) {
y.Left = no
} else {
y.Right = no
}
rbt.count++
rbt.insertFixup(no)
}
func (rbt *Rbtree) insertFixup(no *Node) {
for no.Parent.color == RED {
if no.Parent == no.Parent.Parent.Left {
y := no.Parent.Parent.Right
if y.color == RED {
//
// 情形 4
log.Println("TRACE Do Case 4 :", no.Item)
no.Parent.color = BLACK
y.color = BLACK
no.Parent.Parent.color = RED
no = no.Parent.Parent //循环向上自平衡.
} else {
if no == no.Parent.Right {
//
// 情形 5 : 反向情形
// 直接左旋转 , 然后进行情形3(变色->右旋)
log.Println("TRACE Do Case 5 :", no.Item)
if no == no.Parent.Right {
no = no.Parent
rbt.LeftRotate(no)
}
}
log.Println("TRACE Do Case 6 :", no.Item)
no.Parent.color = BLACK
no.Parent.Parent.color = RED
rbt.RightRotate(no.Parent.Parent)
}
} else { //为父父节点右孩子情形，和左孩子一样，改下转向而已.
y := no.Parent.Parent.Left
if y.color == RED {
no.Parent.color = BLACK
y.color = BLACK
no.Parent.Parent.color = RED
no = no.Parent.Parent
} else {
if no == no.Parent.Left {
no = no.Parent
rbt.RightRotate(no)
}
no.Parent.color = BLACK
no.Parent.Parent.color = RED
rbt.LeftRotate(no.Parent.Parent)
}
}
}
rbt.root.color = BLACK
}
func LeftRotateTest(){
var i10 Int = 10
var i12 Int = 12
rbtree := New()
x := &Node{rbtree.NIL, rbtree.NIL, rbtree.NIL, BLACK, i10}
rbtree.root = x
y := &Node{rbtree.root.Right, rbtree.NIL, rbtree.NIL, RED, i12}
rbtree.root.Right = y
log.Println("root : ", rbtree.root)
log.Println("left : ", rbtree.root.Left)
log.Println("right : ", rbtree.root.Right)
rbtree.LeftRotate(rbtree.root)
log.Println("root : ", rbtree.root)
log.Println("left : ", rbtree.root.Left)
log.Println("right : ", rbtree.root.Right)
}
func RightRotateTest(){
var i10 Int = 10
var i12 Int = 12
rbtree := New()
x := &Node{rbtree.NIL, rbtree.NIL, rbtree.NIL, BLACK, i10}
rbtree.root = x
y := &Node{rbtree.root.Right, rbtree.NIL, rbtree.NIL, RED, i12}
rbtree.root.Left = y
log.Println("root : ", rbtree.root)
log.Println("left : ", rbtree.root.Left)
log.Println("right : ", rbtree.root.Right)
rbtree.RightRotate(rbtree.root)
log.Println("root : ", rbtree.root)
log.Println("left : ", rbtree.root.Left)
log.Println("right : ", rbtree.root.Right)
}
func ItemTest(){
var itype1 Int = 10
var itype2 Int = 12
log.Println(itype1.Less(itype2))
var strtype1 String = "sola"
var strtype2 String = "ailumiyana"
log.Println(strtype1.Less(strtype2))
}
func InsertTest(){
rbtree := New()
rbtree.Insert(&Node{rbtree.NIL, rbtree.NIL, rbtree.NIL, RED, Int(10)})
rbtree.Insert(&Node{rbtree.NIL, rbtree.NIL, rbtree.NIL, RED, Int(9)})
rbtree.Insert(&Node{rbtree.NIL, rbtree.NIL, rbtree.NIL, RED, Int(8)})
rbtree.Insert(&Node{rbtree.NIL, rbtree.NIL, rbtree.NIL, RED, Int(6)})
rbtree.Insert(&Node{rbtree.NIL, rbtree.NIL, rbtree.NIL, RED, Int(7)})
log.Println("rbtree counts : ", rbtree.count)
log.Println("------ ", rbtree.root.Item)
log.Println("----", rbtree.root.Left.Item, "---", rbtree.root.Right.Item)
log.Println("--", rbtree.root.Left.Left.Item, "-", rbtree.root.Left.Right.Item)
}
func main() {
log.Println(" ---- main ------ ")
LeftRotateTest()
RightRotateTest()
ItemTest()
InsertTest()
}
小结
好了本文 对红黑树的讲解到此结束，刚开始看红黑树的时候这些性质确实特别绕，但是理解了这5点性质，就好多了。 然后就是两个操作 ： 变色和旋转 理解红黑树是通过他们进行自平衡的就行了。
由于时间原因只写了插入了 ，没做删除，有机会再补上吧，不过理解了插入原理，删除也不在话下了吧。
红黑树原理详解及golang实现的更多相关文章
- jdk1.8 HashMap红黑树操作详解-putTreeVal()
以前也看过hashMap源码不过是看的jdk1.7的,由于时间问题看的也不是太深入,只是大概的了解了一下他的基本原理:这几天通过假期的时间就对jdk1.8的hashMap深入了解了下,相信大家都是对红 ...
- Java网络编程和NIO详解6：Linux epoll实现原理详解
Java网络编程和NIO详解6:Linux epoll实现原理详解 本系列文章首发于我的个人博客:https://h2pl.github.io/ 欢迎阅览我的CSDN专栏:Java网络编程和NIO h ...
- epoll原理详解及epoll反应堆模型
本文转载自epoll原理详解及epoll反应堆模型 导语 设想一个场景:有100万用户同时与一个进程保持着TCP连接,而每一时刻只有几十个或几百个TCP连接是活跃的(接收TCP包),也就是说在每一时刻 ...
- 【转】VLAN原理详解
1.为什么需要VLAN 1.1 什么是VLAN? VLAN(Virtual LAN),翻译成中文是“虚拟局域网”.LAN可以是由少数几台家用计算机构成的网络,也可以是数以百计的计算机构成的企业网络.V ...
- 0614MySQL的InnoDB索引原理详解
转自http://www.cnblogs.com/shijingxiang/articles/4743324.html MySQL的InnoDB索引原理详解 http://www.admin10000 ...
- VLAN原理详解[转载] 网桥--交换机---路由器
来自:http://blog.csdn.net/phunxm/article/details/9498829 一.什么是桥接 桥接工作在OSI网络参考模型的第二层数据链路层,是一种以 ...
- I2C 基础原理详解
今天来学习下I2C通信~ I2C(Inter-Intergrated Circuit)指的是 IC(Intergrated Circuit)之间的(Inter) 通信方式.如上图所以有很多的周边设备都 ...
- Zigbee组网原理详解
Zigbee组网原理详解 来源:互联网 作者:佚名2015年08月13日 15:57 [导读] 组建一个完整的zigbee网状网络包括两个步骤:网络初始化.节点加入网络.其中节点加入网络又包括两个 ...
- 块级格式化上下文(block formatting context)、浮动和绝对定位的工作原理详解
CSS的可视化格式模型中具有一个非常重要地位的概念——定位方案.定位方案用以控制元素的布局,在CSS2.1中,有三种定位方案——普通流.浮动和绝对定位: 普通流:元素按照先后位置自上而下布局,inli ...
随机推荐
- 遍历json数据的几种方式。
json(JavaScript Object Notation),json是一种多用于存储和交换文本信息的语法.他能够进行数据的传输,通常和ajax一起使用.它具有体积小.速度快,易解析等诸多优点. ...
- 在Tinymce编辑器里，集成数学公式
在以前,需要在Web页面显示数学公式,常用的都是先制作成图片,然后插入到页面里.这使得后期对数学公式的修改变的麻烦,同时也不利于搜索引擎搜索. 本文将介绍如何在TinyMce编辑器里集成数学公式.先看 ...
- 创建自己的github仓库
作者: wangzz 原文地址:http://blog.csdn.net/wzzvictory/article/details/20067595 一.创建自己的github仓库 CocoaPods都托 ...
- react-native修改xcode项目名
目录 1. 选中旧工程名,改为新的工程名 2. 依次选择黄色文件夹,修改名字,千万不要在Xcode外修改!!! 3. 点击Find,点击Find and Replace in Project... 4 ...
- 压缩感知重构算法之OMP算法python实现
压缩感知重构算法之OMP算法python实现 压缩感知重构算法之CoSaMP算法python实现 压缩感知重构算法之SP算法python实现 压缩感知重构算法之IHT算法python实现 压缩感知重构 ...
- Mybatis动态查询
需要导入的jar包: 实体类User: package com.bjsxt.pojo; import java.io.Serializable; public class User implement ...
- Ubuntu18.04安装openCV4.1.2
Ubuntu18.04下安装openCV4.1.2 注意: 在整个安装过程中,包括后期QT的使用中不要出现中文路径.会很坑的. 一.下载openCV4.1.2 可以再官网进行下载https://ope ...
- E - Unimodal Array CodeForces - 831A
Array of integers is unimodal, if: it is strictly increasing in the beginning; after that it is cons ...
- POJ 3660 cow contest （Folyed 求传递闭包）
N (1 ≤ N ≤ 100) cows, conveniently numbered 1..N, are participating in a programming contest. As we ...
- ARTS-S C语言主线程获取子线程返回值
#include<stdio.h> #include<stdlib.h> #include <pthread.h> typedef struct { int stu ...