读《An Adaptable and Extensible Geometry Kernel》

读《An Adaptable and Extensible Geometry Kernel》

利用Curiously Recurring Template Pattern替代虚函数

详细内容可以参考[1]。这里单纯列举出相关的代码示例：

// 使用继承的方式实现不同图形的绘制
class Shape
{
public:
    Shape() {}
    virtual ~Shape() {}
    virtual void Draw() = 0；
};

class Triangle : public Shape
{
public:
    Triangle() {}
    ~Triangle() {}

    void Draw() { cout << "Draw a Triangle" << endl; }
};

class Rectangle : public Shape
{
public:
    Rectangle() {}
    ~Rectangle() {}

    void Draw() { cout << "Draw a Rectangle" << endl; }
};

// 利用Curiously Recurring Template Pattern
template <typename Derived>
class Shape
{
public:
    void Draw()
    {
        return static_cast<Derived*>(this)->Draw();
    }
};

class Triangle : public Shape<Triangle>
{
public:
    void Draw() { cout << "Draw a Triangle" << endl; }
};

class Rectangle : public Shape<Rectangle>
{
public:
    void Draw() { cout << "Draw a Rectangle" << endl; }
};

为什么需要Kernel

通过Kernel需要解决的主要问题是代码的适配性和可扩展性。那为什么可以提高适配性和可扩展性可以在后续的内容中得到答案。

Kernel的概念和架构

常见的数据结构和算法的设计，数据结构为独立的类，算法为全局或类的成员函数。示例如下：

K::Point_2   p(0,1), q(1,-4);   // 数据结构
K::Line_2    line(p,q);

if (less_xy_2(p, q)) { ... }    // 算法成员函数

几何Kernel包含需要操作的类型，以及针对这些类型的操作。Kernel会将上述相关的内容进行打包处理。示例如下:

K k;
K::Construct_line_2  c_line = k.construct_line_2_object();
K::Less_xy_2         less_xy = k.less_xy_2_object();
K::Point_2           p(0,1), q(1,-4);
K::Line_2            line = c_line(p, q);

if (less_xy(p, q)) { ... }

Kernel将数据结构和算法相关的细节放到了内部。整体的架构可以分为三层，Kernel， Geometric Primitives，Numeric Primitives，具体如下：

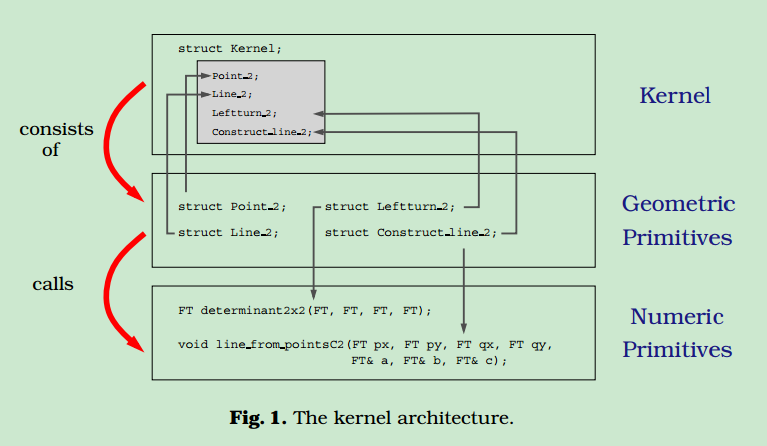
Kernel的实现

第一版本

template <class K> struct MyPoint { };
template <class K> struct MyLine { };
template <class K> struct MyConstruct { };
template <class K> struct MyLess { };

struct Kernel {
    typedef MyPoint<Kernel> Point_2;
    typedef MyLine<Kernel> Line_2;
    typedef MyConstruct<Kernel> Construct_line_2;
    typedef MyLess<Kernel> Less_xy_2;
};

// Generate new Kernel
template <class K> struct NewPoint { };
template <class K> struct MyLeftTurn { };
struct New_kernel : public Kernel {
    typedef NewPoint<New_kernel> Point_2;
    typedef MyLeftTurn<New_kernel> Left_turn_2;
};

int main()
{
    New_kernel::Point_2 p, q;
    New_kernel::Construct_line_2 construct_line_2;
    New_kernel::Line_2 l = construct_line_2(p, q);
    return 0;
}

测试环境可以见： https://ideone.com/MrXCDD

编译错误为：

prog.cpp: In function ‘int main()’:
prog.cpp:28:49: error: no match for call to ‘(Kernel::Construct_line_2 {aka MyConstruct<Kernel>}) (New_kernel::Point_2&, New_kernel::Point_2&)’
     New_kernel::Line_2 l = construct_line_2(p, q);

从编译错误中可见，New_kernel::Construct_line_2其实调用的是MyConstruct<Kernel>的实现，而我们想要的调用是MyConstruct<New_kernel>。依赖关系见下图：

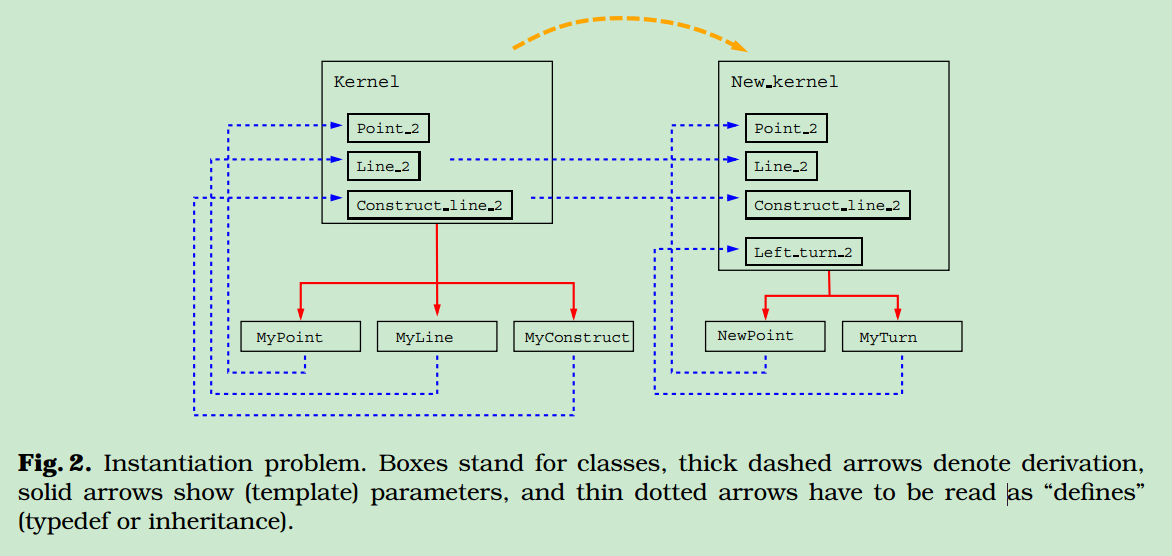
这个版本中另一个隐含的问题是，循环引用的问题，具体如下：

template <class K> struct P {
    typedef K::A B;
};

struct Kernel {
    typedef P<Kernel>::B B;
    typedef int A;
};

为了解决上面的问题，进行了第二版本的改进。

第二版本

为了降低不同Kernel之间的关联性，引入Kernel_base，具体如下：

template <class K> struct MyPoint { };
template <class K> struct MyLine { };
template <class K> struct MyConstruct { };
template <class K> struct MyLess { };

template <class K>
struct Kernel_base {
    typedef MyPoint<K> Point_2;
    typedef MyLine<K> Line_2;
    typedef MyConstruct<K> Construct_line_2;
    typedef MyLess<K> Less_xy_2;
};

struct Kernel : public Kernel_base<Kernel> { };

// Generate new Kernel
template <class K> struct NewPoint { };
template <class K> struct MyLeftTurn { };

template<class K>
struct New_kernel_base : public Kernel_base<K> {
    typedef NewPoint<K> Point_2;
    typedef MyLeftTurn<K> Left_turn_2;
};

struct New_kernel : public New_kernel_base<New_kernel> {};

int main()
{
    New_kernel::Point_2 p, q;
    New_kernel::Construct_line_2 construct_line_2;
    New_kernel::Line_2 l = construct_line_2(p, q);
    return 0;
}

测试环境可以见：https://ideone.com/40wOCa

编译错误如下：

prog.cpp: In function ‘int main()’:
prog.cpp:35:49: error: no match for call to ‘(Kernel_base<New_kernel>::Construct_line_2 {aka MyConstruct<New_kernel>}) (New_kernel_base<New_kernel>::Point_2&, New_kernel_base<New_kernel>::Point_2&)’
     New_kernel::Line_2 l = construct_line_2(p, q);
                                                 ^

从编译结果中可得，Construct_line_2对应的New_kernel正是我们所预期的。接下来需要解决的问题是，construct_line_2并不是可以调用的函数。调整后kernel之间的依赖关系如下：

第三版本

该版本中，利用函数对象来处理操作逻辑。

template <class K> struct MyPoint { };
template <class K> struct MyLine { };
template <class K> struct MyConstruct {
    typedef typename K::Line_2 Line_2;
    typedef typename K::Point_2 Point_2;

    Line_2 operator() (Point_2, Point_2) const
    {
        return Line_2();
    }
};

template <class K> struct MyLess {
    typedef typename K::Point_2 Point_2;

    bool operator() (Point_2, Point_2) const
    {
        return true;
    }
};

template <class K>
struct Kernel_base {
    typedef MyPoint<K> Point_2;
    typedef MyLine<K> Line_2;
    typedef MyConstruct<K> Construct_line_2;
    typedef MyLess<K> Less_xy_2;
    Construct_line_2 construct_line_2_object();
    Less_xy_2        less_xy_2_object();
};

struct Kernel : public Kernel_base<Kernel> { };

// Generate new Kernel
template <class K> struct NewPoint { };
template <class K> struct MyLeftTurn { };

template<class K>
struct New_kernel_base : public Kernel_base<K> {
    typedef NewPoint<K> Point_2;
    typedef MyLeftTurn<K> Left_turn_2;
};

struct New_kernel : public New_kernel_base<New_kernel> {};

int main()
{
    New_kernel::Point_2 p, q;
    New_kernel::Construct_line_2 construct_line_2;
    New_kernel::Line_2 l = construct_line_2(p, q);
    return 0;
}

示例程序见：https://ideone.com/6ISelp

整个编译过程成功通过。

到此处，整个kernel的结构基本完善了。

Kernel使用示例说明算法的适应性

以2D点集凸包计算的实现来举例：https://doc.cgal.org/latest/Convex_hull_2/index.html。仅仅针对算法实现过程中Kernel的使用进行简单说明，对算法的具体实现此处不进行介绍。

// 暴露给外部调用的接口
template <class InputIterator, class OutputIterator>
inline
OutputIterator
ch_graham_andrew( InputIterator first,
                  InputIterator last,
                  OutputIterator result)
{
    typedef std::iterator_traits<InputIterator> ITraits;
    typedef typename ITraits::value_type        value_type;
    typedef CGAL::Kernel_traits<value_type>     KTraits;    // 根据value_type获取KernelTraits
    typedef typename KTraits::Kernel            Kernel;     // 进一步获取Kernel
    return ch_graham_andrew(first, last, result, Kernel()); // 传入Kernel，调用具体实现
}

// 具体实现
template <class InputIterator, class OutputIterator, class Traits>
OutputIterator
ch_graham_andrew( InputIterator  first,
                       InputIterator  last,
                       OutputIterator result,
                       const Traits&  ch_traits)
{
  typedef  typename Traits::Point_2     Point_2;     // 获取Kernel中的类型
  typedef  typename Traits::Equal_2      Equal_2;    // 获取Kernel中的类型

  Equal_2      equal_points = ch_traits.equal_2_object();  // 获取kernel中的算法

  if (first == last) return result;
  std::vector< Point_2 >  V (first, last);
  std::sort( V.begin(), V.end(), ch_traits.less_xy_2_object() ); // 获取Kernel中的算法
  if (equal_points( *(V.begin()), *(V.rbegin())) )
  {
      *result++ = *(V.begin());
      return result;
  }

  #if defined(CGAL_CH_NO_POSTCONDITIONS) || defined(CGAL_NO_POSTCONDITIONS) \
    || defined(NDEBUG)
  OutputIterator  res(result);
  #else
  Tee_for_output_iterator<OutputIterator,Point_2> res(result);
  #endif // no postconditions ...
  ch__ref_graham_andrew_scan( V.begin(), V.end(),  res, ch_traits);
  ch__ref_graham_andrew_scan( V.rbegin(), V.rend(), res, ch_traits);
  CGAL_ch_postcondition( \
      is_ccw_strongly_convex_2( res.output_so_far_begin(), \
                                     res.output_so_far_end(), \
                                     ch_traits));
  CGAL_ch_expensive_postcondition( \
      ch_brute_force_check_2( \
          V.begin(), V.end(), \
          res.output_so_far_begin(), res.output_so_far_end(), \
          ch_traits));
  #if defined(CGAL_CH_NO_POSTCONDITIONS) || defined(CGAL_NO_POSTCONDITIONS) \
    || defined(NDEBUG)
  return res;
  #else
  return res.to_output_iterator();
  #endif // no postconditions ...
}

从上面简单的示例可得，一般在算法构建的时候会在最外层生成调用接口，然后，在具体实现中，通过分别对Kernel中的数据结构和算法的调用，最后组装成一个完整的算法实现。

简单的完整的Kernel

此处将文章最后的示例代码贴出来，用于进一步完善对Kernel的认知。

//------------------------------------------------------------
// bottom layer: number type based function toolbox
//

template <class FT>
FT determinant2x2(FT a00, FT a01, FT a10, FT a11)
{
    return a00*a11 - a10*a01;
}

template <class FT>
void line_from_pointsC2(FT px, FT py, FT qx, FT qy, FT &a, FT &b, FT &c) {}

//------------------------------------------------------------
// mid layer: representations, predicates and constructions
//

template <class K_>
struct Point_2 {
    typedef K_ K;
    typedef typename K::FT FT;
    Point_2() {}
    Point_2(FT x_, FT y_) : x(x_), y(y_) {}
    FT x, y;
};

template <class K_>
struct Line_2 {
    typedef K_ K;
    typedef typename K::Point_2 Point_2;
    Line_2() {}
    Line_2(Point_2 p, Point_2 q) { *this = K::Construct_line_2(p,q); }
    typename K::FT a, b, c;
};

template <class K_>
struct Segment_2 {
    typedef K_ K;
    typename K::Point_2 s, e;
};

template <class K_>
struct Less_xy_2 {
    typedef typename K_::Point_2 Point_2;
    bool operator()(Point_2 p, Point_2 q) const
    { return p.x < q.x || p.x == q.x && p.y < q.y; }
};

template <class K_>
struct Left_turn_2 {
    typedef typename K_::Point_2 Point_2;
    bool operator()(Point_2 p, Point_2 q, Point_2 r) const
    {
        return determinant2x2(q.x - p.x, q.y - p.y,
                              r.x - p.x, r.y - q.y) > 0;
    }
};

template <class K_>
struct Construct_line_2 {
    typedef typename K_::Point_2 Point_2;
    typedef typename K_::Line_2 Line_2;
    Line_2 operator()(Point_2 p, Point_2 q) const {
        Line_2 l;
        Line_from_pointsC2(p.x, p.y, q.x, q.y, l.a, l.b, l.c);
        return l;
    }
};

//------------------------------------------------------------
// top layer: geometric kernel
//

template <class K_, class FT_>
struct Kernel_bae {
    typedef K_                           K;
    typedef FT_                          FT;
    typedef Point_2<K>                   Point_2;
    typedef Line_2<K>                    Line_2;
    typedef Segment_2<K>                 Segment_2;
    typedef Less_xy_2<K>                 Less_xy_2;
    typedef Left_turn_2<K>               Left_turn_2;
    typedef Construct_line_2<K>          Construct_line_2;

    Less_xy_2 less_xy_2_object() const { return Less_xy_2(); }
    Left_turn_2 Left_turn_2_object() const { return Left_turn_2(); }
    Construct_line_2 construct_line_2_object() const { return Construct_line_2(); }
};

template <class FT_>
struct Kernel : public Kernel_base<Kernel<FT_>, FT_>
{};

//------------------------------------------------------------
// convenience layer: global functions
//

template < class K >inline
bool
less_xy_2(typename K::Point_2 p,typename K::Point_2 q, K k = K())
{ returnk.less_xy_2_object()(p, q); }

template < class K >inline
bool
left_turn_2(typenameK::Point_2 p,
            typenameK::Point_2 q,
            typenameK::Point_2 r,
            K k = K())
{ returnk.left_turn_2_object()(p, q, r); }

//------------------------------------------------------------
// enve more convenience: specializations for kernel
//

template < class FT > inline
bool
left_turn_2(Point_2< Kernel< FT > > p,
            Point_2< Kernel< FT > > q,
            Point_2< Kernel< FT > > r)
{ returnleft_turn_2(p, q, r, Kernel< FT >()); }

template < class FT >inline
bool
less_xy_2(Point_2< Kernel< FT > > p, Point_2< Kernel< FT > > q)
{ returnless_xy_2(p, q, Kernel< FT >()); }

参考

• [1] https://www.geeksforgeeks.org/curiously-recurring-template-pattern-crtp-2/
• [2] An Adaptable and Extensible Geometry Kernel https://inf.ethz.ch/~hoffmann/pub/hhkps-aegk-01a.pdf