18.10.7 POIN 模拟赛

期望：80+ +90+40=210+

实际：30+90+0=120

链接：https://www.nowcoder.com/acm/contest/175/A
来源：牛客网

时间限制：C/C++ 1秒，其他语言2秒
空间限制：C/C++ 262144K，其他语言524288K
64bit IO Format: %lld

题目描述

CJK 是一个喜欢数据结构的同学。一天他看到 BZOJ 4012 这一题。“这似乎可以用动态点分治做。”，他想。然而他并不会动态点分治，因此他拿着这一题去问 XXX。

然而 XXX 跟他说：“你呀，毕竟图样图森破，上台拿衣服！连基础都没学好，就想学这些高端的东西！来，我这里有一题，如果你能把这道题秒掉，我才能教你动态点分治！”

于是 CJK 打开题目。题目很短，只有一句话：

“给出 l, r, k，请从小到大输出所有在 [l, r] 范围内，能表示为 k 的非负整数次方的所有数。”

“多组数据。”，XXX 补充说，“注意所有数的 0 次方都为 1，因此 1 也得算进去哦。”

输入描述:

第一行一个数 T，表示数据组数。

接下来 T 行，每行 3 个数 l,r,k，表示一组数据。

输出描述:

对于每一组数据输出一行（总共输出 T 行）。

如果存在符合要求的数，则在一行内从小到大输出这些数；否则输出一个字符串 "None."（包括句点，不包括引号）。

输入例子:

4

1 10 2

2 4 5

19562 31702689720 17701

3680 37745933600 10

输出例子:

1 2 4 8

None.

313325401

10000 100000 1000000 10000000 100000000 1000000000 10000000000

-->

示例1

输入

复制

4

1 10 2

2 4 5

19562 31702689720 17701

3680 37745933600 10

输出

复制

1 2 4 8

None.

313325401

10000 100000 1000000 10000000 100000000 1000000000 10000000000

备注:

/*

也就是到1e18 再大就跑不动了，

所以就看出题人的数据范围了，

如果小的话还可以，大了就gg了。

long long相乘太耗时间了。

正常计算是最慢 63*10^4

但是long long 跑不出来啊！！ 

还很担心会不会有两数相乘爆long long

成了负数，那while就跑不出来了。

*/

#include<cmath>

#include<queue>

#include<cstdio>

#include<cstdlib>

#include<cstring>

#include<iostream>

#include<algorithm>

using namespace std;

int T;

long long l,r,k,sum;

int main(){

    scanf("%d",&T);

    while(T--){

        sum=;bool f=;

        scanf("%lld%lld%lld",&l,&r,&k);

        if(k==){

            if(l==&&r==)    printf("None.\n");    /*此处在挂掉50分*/

            else if(l<=) printf("1\n");

            else printf("None.\n");

            continue;

        }

        if(k==){

            if(l==&&r==)    printf("0\n");

            else if(l==&&r!=)    printf("0 1 \n");    /*此处由于眼瞎挂掉40分*/

            else if(l==)   printf("1 \n");

            else printf("None.\n");

            continue;

        }

        while(){

            if(sum>=l&&sum<=r){

                printf("%lld ",sum);

                f=;

            }

               if(r/k<sum)    break;        //此处挂掉50分

            sum*=k;

        }

        if(f==)    printf("None.\n");

        else printf("\n");

    }

}

/*

所以本题期望80+ 实际30分

失分原因：l ≤r，0≤l,r,k <2^63。

此处的 l<=r 看成了 1<=r 漏判了50分的情况。

其次 是while的结束条件 if(r/k<sum)    break;

应该是炸了 long long 导致死循环 炸掉50分。

综合炸掉70分。。。。。~~~~(>_<)~~~~

*/

链接：https://www.nowcoder.com/acm/contest/175/B
来源：牛客网

时间限制：C/C++ 1秒，其他语言2秒
空间限制：C/C++ 524288K，其他语言1048576K
64bit IO Format: %lld

题目描述

给出一个序列 a₁, ..., a_n。

定义一个区间 [l,r] 是好的，当且仅当这个区间中存在一个 i，使得 a_i 恰好等于 a_l, a_l+1, ..., a_r-1, a_r 的最大公因数。

求最长的好的区间的长度。

输入描述:

第一行 n，表示序列的长度；

第二行 n 个数

输出描述:

输出一行一个数，表示最长的好的区间的长度。

输入例子:

5

4 6 9 3 6

输出例子:

-->

示例1

输入

复制

5

4 6 9 3 6

输出

复制

说明

选择区间 [2,5]，i=4。

备注:

/*

题目要求很显然是求最长的一个区间且这个区间中所有的数都是最小的数的倍数。

从左向右扫，对每个点向左拓展它能到达的最长长度，因为要求是倍数，所以如

果遇到起倍数，直接把他倍数所能拓展到的长度接上，如果不是就停止。

然后从右向左扫 同理。

最后统计。 

期望得分 ：90

*/

#include<cmath>

#include<queue>

#include<cstdio>

#include<cstdlib>

#include<cstring>

#include<iostream>

#include<algorithm>

#define MAXN 4000001

using namespace std;

int n,ans;

int l[MAXN],r[MAXN];

long long a[MAXN];

int main(){

    scanf("%d",&n);

    for(int i=;i<=n;i++)

        scanf("%lld",&a[i]);

    for(int i=;i<=n;i++)

        for(int j=i-;j>=;j--){

            if(a[j]%a[i]==){ l[i]+=l[j]+;j=j-l[j]; }

            else if(a[j]%a[i]!=)    break;

        }

    for(int i=n;i>=;i--)

        for(int j=i+;j<=n;j++){

            if(a[j]%a[i]==){ r[i]+=r[j]+;j=j+r[j]; }

            else if(a[j]%a[i]!=)    break;

        }

    for(int i=;i<=n;i++)

        ans=max(ans,l[i]+r[i]+);

    printf("%d\n",ans);

}

/*期望得分 90  实际得分 90*/

我这个方法的时间复杂度应该是O(n log n)的。

题解是这么写的

这个人↓的写法和我一样，但是不知道加了个什么奇奇怪怪的优化，竟然AC了我这决不是嫉妒（扎小人）

#include<iostream>

#include<cstdio>

#include<algorithm>

using namespace std;

const int wx=;

inline char get_char(){

    static char buf[],*p1=buf,*p2=buf;

    return p1==p2&&(p2=(p1=buf)+fread(buf,,,stdin),p1==p2)?EOF:*p1++;

}

#define short long long

inline short read(){

    short num=;

    char c;

    while(!isdigit(c=get_char()));

    for(num=c-;isdigit(c=get_char());num=((num+(num<<))<<)+c-);

    return num;

}

long long a[wx];

int l[wx],r[wx];

int n;

int ans;

signed main(){

    ios::sync_with_stdio(false);

    cin.tie();cout.tie();

    cin>>n;

    for(int i=;i<=n;i++)    cin>>a[i];

    for(int i=;i<=n;i++)

        for(l[i]=i;l[i]>&&a[l[i]-]%a[i]==;l[i]=l[l[i]-]);

    for(int i=n;i>=;i--)

        for(r[i]=i;r[i]<n&&a[r[i]+]%a[i]==;r[i]=r[r[i]+]);

    for(int i=;i<=n;i++)

        ans=max(ans,r[i]-l[i]+);

    printf("%d\n",ans);

    return ;

}

后来发现我和AC之间就差了几个优化。

#include<cmath>

#include<queue>

#include<cstdio>

#include<cstdlib>

#include<cstring>

#include<iostream>

#include<algorithm>

#define MAXN 4000001

using namespace std;

template<typename T>

inline void read(T&w){

    char c;

    while(!isdigit(c=getchar()));w=c&;

    while(isdigit(c=getchar()))w=w*+(c&);

}

inline char smax(int&x,const int&y){return x<y?x=y,:;}

int n,ans;

int l[MAXN],r[MAXN];

long long a[MAXN];

int main(){

    read(n);

    for(int i=;i<=n;i++)

        read(a[i]);

    for(int i=;i<=n;i++)

        for(int j=i-;j>=;j--){

            if(a[j]%a[i]==){ l[i]+=l[j]+;j=j-l[j]; }

            else if(a[j]%a[i]!=)    break;

        }

    for(int i=n;i>=;i--)

        for(int j=i+;j<=n;j++){

            if(a[j]%a[i]==){ r[i]+=r[j]+;j=j+r[j]; }

            else if(a[j]%a[i]!=)    break;

        }

    for(int i=;i<=n;i++)

        smax(ans,r[i]+l[i]+);

    printf("%d\n",ans);

}

这里面那些我也看不懂的东西就是加的优化。

链接：https://www.nowcoder.com/acm/contest/175/C
来源：牛客网

时间限制：C/C++ 2秒，其他语言4秒
空间限制：C/C++ 524288K，其他语言1048576K
64bit IO Format: %lld

题目描述

你需要在一条无限长的道路上喷洒杀虫剂。

在这条道路上，总共有 N 个投放点，其中第 i 个投放点在数轴上坐标 p_i 处。在每一个投放点，你可以选择往左喷洒或往右喷洒。但是由于风向和地理环境的影响，向左喷洒和向右喷洒的效果不一定相同。具体来说，在一个位置向左喷洒，可以覆盖 [p_i - l_i, p_i] 这一段区域，而向右喷洒可以覆盖 [p_i, p_i + r_i] 这一段区域。

请你决定每个投放点是向左喷洒还是向右喷洒，来使得被杀虫剂覆盖的路段长度和最大。

输入描述:

第一行 N。
接下来 N 行，每行

输出描述:

输出最大的被杀虫剂覆盖的长度和。

输入例子:

输出例子:

-->

示例1

输入

复制

输出

复制

说明

让第一个和第三个投放点向左喷洒，其他投放点向右喷洒。

这样能覆盖的区域是 $[-1,8]$，总长度为 9。

备注:

 
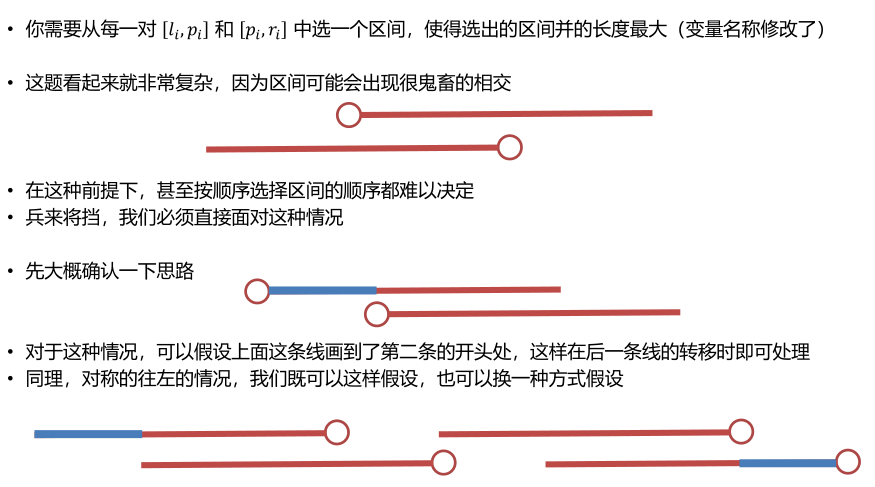
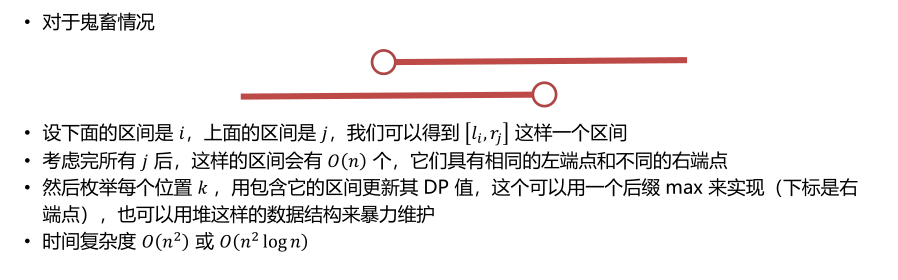
感觉是个DP但是只能想出三维的，所以就写了线段树。
f[i][j][k]表示到第i个为止有j个向左，k个向右所能覆盖的最长长度，然后就没写。
期望40 实际 0
QwQ 好吧。。。我本来就没对线段树抱多大期望。。。。

/*

首先 对于第3.4个测试点的20分的暴力是很好想的 因为他的ri全部是0

然后是1.2号测试点可以暴力一下看看每个点是向左还是向右，

时间复杂度大约是O(2^n);

至于修改操作，当然不能挨着修改，挨着查询，赶脚可以用（线段树）搞一下。

但是看看区间长度，感觉需要离散化搞一下，但我离散写的不好，就不写了。

期望得分 40;

*/

#include<cmath>

#include<queue>

#include<cstdio>

#include<cstdlib>

#include<cstring>

#include<iostream>

#include<algorithm>

using namespace std;

int n,R=;

long long ans;

int decide[];

struct nond{

    int p,l,r;

}v[];

struct non{

    int l,r,flag,dis;

}tree[*];

void up(int now){

    tree[now].dis=tree[now*].dis+tree[now*+].dis;

}

void build(int now,int l,int r){

    tree[now].l=l;tree[now].r=r;

    tree[now].flag=;

    if(tree[now].l==tree[now].r){

        tree[now].dis=;

        return ;

    }

    int mid=(tree[now].l+tree[now].r)/;

    build(now*,l,mid);

    build(now*+,mid+,r);

    up(now);

}

void down(int now){

    tree[now*].flag=;tree[now*+].flag=;

    tree[now*].dis=tree[now*].r-tree[now*].l+;

    tree[now*+].dis=tree[now*+].r-tree[now*+].l+;

    tree[now].flag=;

}

void change(int now,int optl,int optr){

    if(tree[now].l==optl&&tree[now].r==optr){

        tree[now].dis=tree[now].r-tree[now].l+;

        tree[now].flag=;

        return ;

    }

    if(tree[now].flag)    down(now);

    int mid=(tree[now].l+tree[now].r)/;

    if(optr<=mid)    change(now*,optl,optr);

    else if(optl>mid)    change(now*+,optl,optr);

    else {

        change(now*,optl,mid);

        change(now*+,mid+,optr);

    }

    up(now);

}

long long work(){

    for(int i=;i<=n;i++)

        if(decide[i]==-)    change(,v[i].p-v[i].l,v[i].p);

        else if(decide[i]==)    change(,v[i].p,v[i].p+v[i].r);

    return tree[].dis;

}

void dfs(int tot,int now){

    if(now==tot+){

        ans=max(ans,work());

        build(,,R);

        return ;

    }

    decide[now]=-;dfs(tot,now+);decide[now]=;

    decide[now]=;dfs(tot,now+);decide[now]=;

}

int main(){

    scanf("%d",&n);int add=,sum=;

    for(int i=;i<=n;i++){

        scanf("%d%d%d",&v[i].p,&v[i].l,&v[i].r);

        if(v[i].p-v[i].l<)    add=v[i].l-v[i].p+;

        if(v[i].r==)    sum++;

        R=max(R,v[i].p+v[i].r);

    }

    for(int i=;i<=n;i++)    v[i].p+=add;

    R+=add;

    build(,,R);

    if(n<=){

        dfs(n,);

        printf("%lld",ans-);

    }

    else if(sum==n){

        for(int i=;i<=n;i++)

            change(,v[i].p-v[i].l,v[i].p);

        printf("%lld",tree[].dis-);

    }

}

#include<cstdio>

#include<cstring>

#include<iostream>

#include<algorithm>

#define MAXN 3010

using namespace std;

int N,H;

int f[MAXN][MAXN*];

int h[MAXN*],P[MAXN*],L[MAXN*];

struct nond{

    int p,l,r;

}v[MAXN];

int cmp(nond a,nond b){

    return a.p<b.p;

}

int main(){

    scanf("%d",&N);

    for(int i=;i<=N;i++){

        scanf("%d%d%d",&v[i].p,&v[i].l,&v[i].r);;

        h[++H]=v[i].p-v[i].l;

        h[++H]=v[i].p;

        h[++H]=v[i].p+v[i].r;

    }

    sort(v+,v++N,cmp);

    sort(h+,h+H+);

    H=unique(h+,h+H+)-h-;

    for(int i=;i<=N;i++){

        int id=lower_bound(h+,h+H+,v[i].p)-h;

        P[id]=i;

        L[id]=lower_bound(h+,h+H+,v[i].p-v[i].l)-h;

    }

    for(int i=;i<=N;i++){

        const int p=lower_bound(h+,h+H+,v[i].p)-h;

        const int l=lower_bound(h+,h+H+,v[i].p-v[i].l)-h;

        const int r=lower_bound(h+,h+H+,v[i].p+v[i].r)-h;

        int *F=::f[i];//??可能是定义一个数组F,f

        const int *G=::f[i-],hp=h[p];

        memcpy(F+,G+,H<<);

        for(int j=l+;j<=p;j++)

            F[j]=max(F[j],F[j-]+h[j]-h[j-]);

        for(int j=p+,Max=G[p];j<=r;j++){

            F[j]=max(F[j],Max+h[j]-hp);

            if(P[j]&&L[j]<p)

                Max=max(Max,hp-h[L[j]]+G[L[j]]);

        }

        for(int j=;j<=H;j++)

            F[j]=max(F[j],F[j-]);

    }

    printf("%d\n",f[N][H]);

}