Leetcode 310.最小高度树

最小高度树

对于一个具有树特征的无向图，我们可选择任何一个节点作为根。图因此可以成为树，在所有可能的树中，具有最小高度的树被称为最小高度树。给出这样的一个图，写出一个函数找到所有的最小高度树并返回他们的根节点。

格式

该图包含 n 个节点，标记为 0 到 n - 1。给定数字 n 和一个无向边 edges 列表（每一个边都是一对标签）。

你可以假设没有重复的边会出现在 edges 中。由于所有的边都是无向边，[0, 1]和 [1, 0] 是相同的，因此不会同时出现在 edges 里。

示例 1:

输入: n = 4, edges = [[1, 0], [1, 2], [1, 3]]

输出: [1]

示例 2:

输入: n = 6, edges = [[0, 3], [1, 3], [2, 3], [4, 3], [5, 4]]

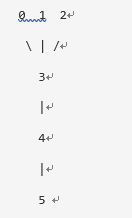
输出: [3, 4]

说明:

• 根据树的定义，树是一个无向图，其中任何两个顶点只通过一条路径连接。换句话说，一个任何没有简单环路的连通图都是一棵树。
• 树的高度是指根节点和叶子节点之间最长向下路径上边的数量。

解题思路

常规方法可以使用BFS或者DFS，对每个点都遍历一遍，求出所有点组成的树的高度，然后找出哪些高度最小的节点，可以通过不断更新最低高度来进行剪枝。但是时间复杂度过高。

最终的解题思路采用了不断删除叶子节点，逐渐逼近根节点的方法，在删除叶子节点的同时，会有一些新的节点成为叶子节点，于是继续循环删除，直至不能删除为止，那么剩下的节点就是高度最小的根。

首先将图存储起来，并将每个节点的入度存储起来，然后遍历将入度为1（叶节点）的节点加入队列。

bfs，当队列不空，取队列存储过的叶子节点再将叶子节点的邻接节点，如果邻接节点的度也为1（叶子节点），加入队列。

如此反复，直到减掉所有叶子节点最后一批剩下来的就是正确答案。

 import java.util.ArrayDeque;
 import java.util.ArrayList;
 import java.util.List;
 import java.util.Queue;

 public class Solution {
     public List<Integer> findMinHeightTrees(int n, int[][] edges) {
         List<List<Integer>> map = new ArrayList<List<Integer>>();
         List<Integer> res = new ArrayList<Integer>();
         if (n==1) {
             res.add(0); return res;
         }
         //记录每个点的入度
         int[] degree = new int[n];
         for (int i = 0;i < n;i++ ) {
             map.add(new ArrayList<Integer>());
         }
         for (int i = 0;i< edges.length;i++) {
             map.get(edges[i][0]).add(edges[i][1]);
             map.get(edges[i][1]).add(edges[i][0]);
             degree[edges[i][0]]++;
             degree[edges[i][1]]++;
         }
         Queue<Integer> q = new ArrayDeque<Integer>();
         for (int i = 0;i < n;i++ ) {
             if(degree[i] == 0) {
                 return res;
             } else if(degree[i] == 1) {
                 q.offer(i);
             }
         }
         while(!q.isEmpty()) {
             res = new ArrayList<Integer>();
             int count = q.size();
             for (int i = 0;i < count ;i++ ) {
                 int cur = q.poll();
                 res.add(cur);
                 degree[cur]--;
                 for (int k = 0;k < map.get(cur).size() ;k++ ) {
                     int next = map.get(cur).get(k);
                     degree[next]--;
                     if(degree[next] == 1) {
                         q.offer(next);
                     }
                 }
             }
         }
         return res;
     }
 }