Tree 树（树形期望dp）

题意也是需要解释一下的，这个期望步数，是需要求无限步的时候的，就是你只要能到达，都要算上去，

这个我一开始真的没什么思路，打了暴力，搞一个精度，结果全超时了，看来精度定的太细了。

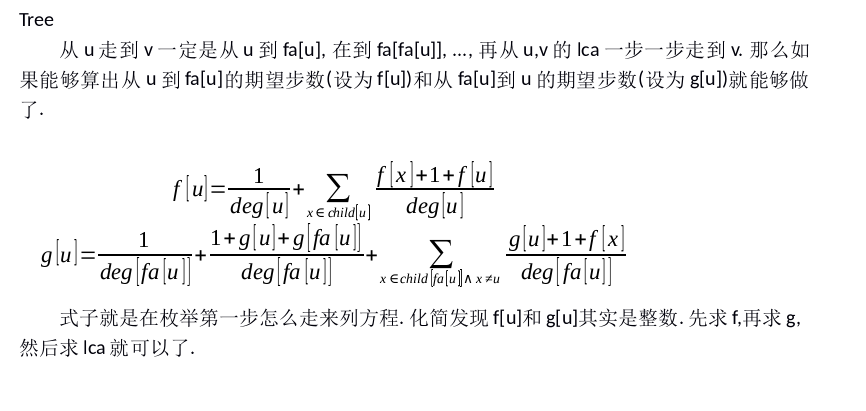
出题人的题解是这个，的确还是难以理解的，说明出题人水平十分高，死磕了。

deg数组是度的意思

看一下这个图片

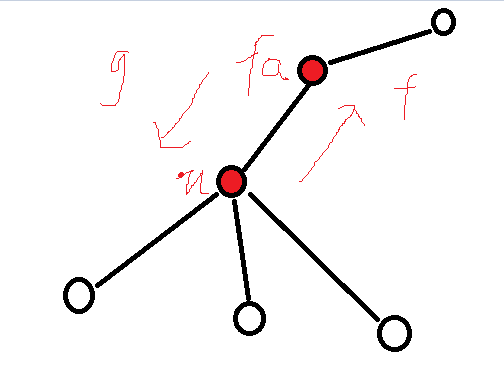
我们看一下关于 f 这个式子，第一项表示直接到其父亲，这个是十分显然的，后者就是先到其儿子，在到儿子的父亲，也就是

自己，然后的期望步数+1就是其到儿子那一步，然后在去u的父亲就好了。

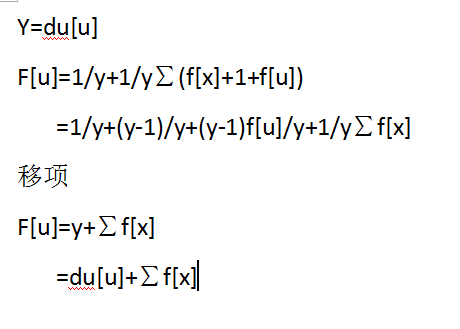
过程是这个，应该还是可以理解了吧，这样发现右边无小数了。

g数组的话第一项就是直接下来，第二项就是从其父亲下来，第三项就是从其兄弟那里过来，如果理解了f应该好理解g的。

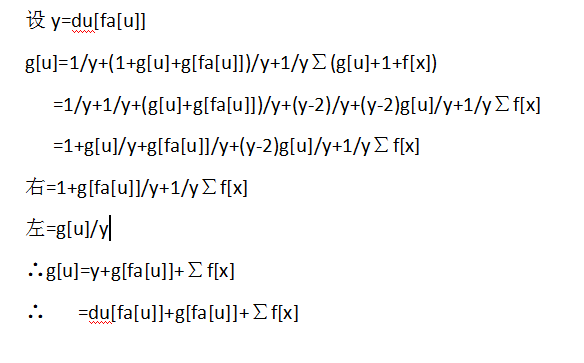
处理好g和f数组以后就可以搞了，因为其符合加法，所以只需要求个前缀和就好了，

就是到该节点的f,g的和，然后求个lca剪一剪，加一加就没了。

O(∩_∩)O哈！