poj 1486 Sorting Slides

Sorting Slides

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 4469		Accepted: 1766

Description

Professor Clumsey is going to give an important talk this afternoon. Unfortunately, he is not a very tidy person and has put all his transparencies on one big heap. Before giving the talk, he has to sort the slides. Being a kind of minimalist, he wants to do this with the minimum amount of work possible.

The situation is like this. The slides all have numbers written on them according to their order in the talk. Since the slides lie on each other and are transparent, one cannot see on which slide each number is written.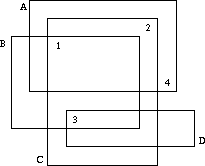 

Well, one cannot see on which slide a number is written, but one may deduce which numbers are written on which slides. If we label the slides which characters A, B, C, ... as in the figure above, it is obvious that D has number 3, B has number 1, C number 2 and A number 4.

Your task, should you choose to accept it, is to write a program that automates this process.

Input

The input consists of several heap descriptions. Each heap descriptions starts with a line containing a single integer n, the number of slides in the heap. The following n lines contain four integers xmin, xmax, ymin and ymax, each, the bounding coordinates of the slides. The slides will be labeled as A, B, C, ... in the order of the input.

This is followed by n lines containing two integers each, the x- and y-coordinates of the n numbers printed on the slides. The first coordinate pair will be for number 1, the next pair for 2, etc. No number will lie on a slide boundary.

The input is terminated by a heap description starting with n = 0, which should not be processed.

Output

For each heap description in the input first output its number. Then print a series of all the slides whose numbers can be uniquely determined from the input. Order the pairs by their letter identifier.

If no matchings can be determined from the input, just print the word none on a line by itself.

Output a blank line after each test case.

Sample Input

4
6 22 10 20
4 18 6 16
8 20 2 18
10 24 4 8
9 15
19 17
11 7
21 11
2
0 2 0 2
0 2 0 2
1 1
1 1
0

Sample Output

Heap 1
(A,4) (B,1) (C,2) (D,3)

Heap 2
none

题意：有n张幻灯片重叠在了一起，并且每张幻灯片上都标记了一个数字，只是重叠之后不知道相应的数字是哪张幻灯片上的，你需要判断那几张幻灯片可以确定出它们上面标记的数字。
思路：每张幻灯片抽象为一个结点，每个数字也抽象为一个结点，并且每个数字出现在了某张幻灯片的内部，幻灯片就向该数字连一条边，这样建立了匹配图，之后就是二分匹配问题。先求一次该图最大匹配，求得的匹配数设为N；
要确定出每张幻灯片a是不是对应了某个数字b，可以先把a,b对应的边从图中删除，删除后再求该图最大匹配，若最大匹配变为了N-1，说明这条边是必须边，即确定了a,b的对应关系；反之，这条边删除后，a还可以和其他的数字对应，b还可和其他幻灯片对应，那么关系就不唯一了，无法确定。操作完成，把这条边再加进图中
把所有边都删除一次，即可确定哪些边是必须的。
AC代码：

#define _CRT_SECURE_NO_DEPRECATE
#include<iostream>
#include<algorithm>
#include<queue>
#include<set>
#include<vector>
#include<cstring>
#include<string>
using namespace std;
#define INF 0x3f3f3f3f
const int N_MAX =;
int V;//点的个数
vector<int>G[N_MAX];
int match[N_MAX];
bool used[N_MAX];
void add_edge(int u, int v) {
    G[u].push_back(v);
    G[v].push_back(u);

}

bool dfs(int v) {
    used[v] = true;
    for (int i = ; i < G[v].size(); i++) {
        int u = G[v][i], w = match[u];
        if (w <  || !used[w] && dfs(w)) {
            match[v] = u;
            match[u] = v;
            return true;
        }
    }
    return false;
}

int bipartite_matching() {
    int res = ;
    memset(match, -, sizeof(match));
    for (int v = ; v < V; v++) {
        if (match[v] < ) {
            memset(used, , sizeof(used));
            if (dfs(v))
                res++;
        }
    }
    return res;
}

struct Area {
    int x_min, x_max, y_min, y_max;

}area[N_MAX];
struct Cor {
    int x, y;
}cor[N_MAX];
int n,s,t,COr[N_MAX];
char ARea[N_MAX];
int main() {
    int Case = ;
    while (scanf("%d",&n)&&n) {
        Case++;
        //0~n-1:区域
        //n~2n-1:记号
        V =  * n;
        for (int i = ; i < n; i++)
            scanf("%d%d%d%d",&area[i].x_min,&area[i].x_max,&area[i].y_min,&area[i].y_max);
        for (int i = ; i < n;i++) {
            scanf("%d%d",&cor[i].x,&cor[i].y);
            for (int j = ; j < n;j++) {
                if (area[j].x_min<cor[i].x&&area[j].x_max>cor[i].x&&area[j].y_min<cor[i].y&&area[j].y_max>cor[i].y)
                add_edge(j, i + n);
            }
        }
        int N = bipartite_matching();//一开始匹配数
        int num = ;
        for (int i = ; i < n;i++) {//对于每一块区域
            for (int j = ; j < n;j++) {//对于每一个坐标点
                if (area[i].x_min<cor[j].x&&area[i].x_max>cor[j].x&&area[i].y_min<cor[j].y&&area[i].y_max>cor[j].y) {
                    vector<int>::iterator it1 = find(G[i].begin(),G[i].end(),j+n);
                    vector<int>::iterator it2 = find(G[j + n].begin(), G[j + n].end(), i);
                    G[i].erase(it1);
                    G[j + n].erase(it2);
                    if (bipartite_matching() < N) {//说明是必须边
                        ARea[num] = i+;
                        COr[num] = j+;
                            num++;
                    }
                    add_edge(i, j + n);//复原
                }
            }
        }

        if (!num)printf("Heap %d\nnone\n",Case);
        else {
            printf("Heap %d\n", Case);
            for (int i = ; i < num;i++) {
                printf("(%c,%d) ",ARea[i],COr[i]);
            }
            puts("");
        }
        puts("");
    for (int i = ; i < V;i++) {
            G[i].clear();
        }
    }
    return ;
}