【2018.10.18】noip模拟赛Day2 地球危机（2018年第九届蓝桥杯C/C++A组省赛 三体攻击）

题目描述

三体人将对地球发起攻击。为了抵御攻击，地球人派出了 $A × B × C$ 艘战舰，在太 空中排成一个 $A$ 层 $B$ 行 $C$ 列的立方体。其中，第 $i$ 层第 $j$ 行第 $k$ 列的战舰（记为战舰 $d(i, j,k)$）的生命值为 $d_{i, j,k}$。

三体人将会对地球发起 m 轮“立方体攻击”，每次攻击会对一个小立方体中的所有 战舰都造成相同的伤害。具体地，第 t 轮攻击用 7 个参数 $la_t ,ra_t , lb_t ,rb_t , lc_t ,rc_t , h_t$ 描述； 所有满足 $i ∈ [la_t ,ra_t], j ∈ [lb_t,rb_t], k ∈ [lc_t,rc_t]$ 的战舰 $(i, j, k)$ 会受到 $h_t$ 的伤害。如果一个 战舰累计受到的总伤害超过其生命值，那么这个战舰会爆炸。

地球指挥官希望你能告诉他，第一艘爆炸的战舰是在哪一轮攻击后爆炸的。

输入格式

从文件 attack.in 中读入数据。

第一行包括 4 个正整数 $A,B,C,m$；

第二行包含 $A × B × C$ 个整数，其中第 $((i − 1) × B + (j − 1)) × C + (k − 1) + 1$ 个数 为 $d_{i,j,k}$；

第 3 到第 $m + 2$ 行中，第 $t − 2$ 行包含 $7$ 个正整数 $la_t ,ra_t , lb_t ,rb_t , lc_t ,rc_t , h_t$。

输出格式

输出到文件 attack.out 中。

输出第一个爆炸的战舰是在哪一轮攻击后爆炸的。保证一定存在这样的战舰。

样例 1 输入

2 2 2 3
1 1 1 1 1 1 1 1
1 2 1 2 1 1 1
1 1 1 2 1 2 1
1 1 1 1 1 1 2

样例 1 输出

2

样例 1 解释

在第 $2$ 轮攻击后，战舰 $(1, 1, 1)$ 总共受到了 $2$ 点伤害，超出其防御力导致爆炸。

子任务

对于 $10\%$ 的数据，$B = C = 1$；

对于 $20\%$ 的数据，$C = 1$；

对于 $40\%$ 的数据，$A × B × C, m ≤ 10, 000$；

对于 $70\%$ 的数据，$A,B,C ≤ 200$；

对于所有数据，$A × B × C ≤ 10^6 , m ≤ 10^6 , 0 ≤ d_{i, j,k},h_t ≤ 10^9$。

题解

讲道理，这应该是网上第一篇详细讲这题的题解了。

之前翻这题题解的时候，大部分人都“只打了过70分的暴力”（实际上是50分复杂度的），好像还有人说若有时间复杂度更低的做法，请指教……

那这就是他需要的做法了吧。

50pts

随便$O(ABC*m)$的暴力就行。

100pts

首先说一下，满分做法不需要数据结构，更不需要什么三维线段树，应该没超过省选难度。

但是比较难想，亲自做一下就能体验到。

这种题显然是有单调性的，即飞船不会加血，如果它在某一秒被打到0血以下，那它以后就一直在0血以下了。

所以可以二分答案（攻击次数），然后判断此时是否存在血量$\lt 0$ 的飞船，如果有就降低答案的二分范围，没有就升高答案的二分范围。

虽然存在单调性，但二分判断好像还得暴力进行每次攻击操作，于是二分就没用了。

简单地说，要让二分上场，我们就得用$O(m)$的时间求出$m$次操作后所有飞船剩余的血量。

三维区间减法的不好想，可以先降为一维。

一维区间减法除了用段树之外，还有什么方法维护？

差分！

差分具体是个什么东西？

给你一个序列$a$，设一个序列$s$为$a$序列中相邻两个数的差，即$s(i)=a(i)-a(i-1)$。特别的，未赋值的$a(0)$为$0$。

我们发现，这样一个数就可以用前面所有的差的和来表示，即$a(i)\space =\space a(i)-a(i-1)+a(i-1)-a(i-2)+...+a(1)-a(0)\space =\space s(i)+s(i-1)+...+s(1)$

这就是差的前缀和。

如果我们只想快速得到少量位置的当前数的话，应该用树状数组维护差分。

但我们现在需要知道所有的数（判断是否存在小于$0$的数），就没必要再用一个$log$维护了，直接线性递推$s(i)$求出每个$a(i)$。

这样有什么好处呢？

当进行区间减法（区间加法同理）时，区间内的数彼此的相对差是不变的（都减少了同一个值，差没变），只有两端的差变了。所以每次区间减法只需要修改两端的差分值。

比如有个数列$a$：1 2 3 2 3 1

对应的差分值$s$：1 1 1 -1 1 -2

现在让$[3,5]$区间都$-1$。

只有$2,3$和$5,6$的差变了，$a(3)-a(2)$减少了$1$，$a(6)-a(5)$增加了$1$。

于是直接修改第$3$和第$6$个位置的差分值。

难度升级，考虑二维。

二维的差分变化情况就是这样

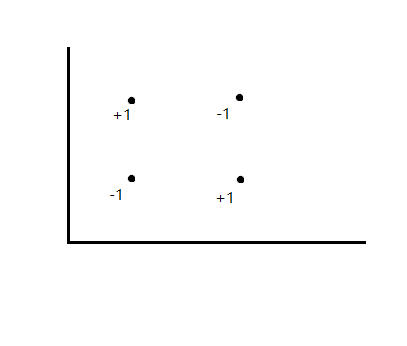
比如一次操作要把图中四个点形成的矩形区间的所有值$-1$，那每个角点的差分值变化就是点旁标的数字。

再推广到三维，就是这样（我还亲自连了线……）

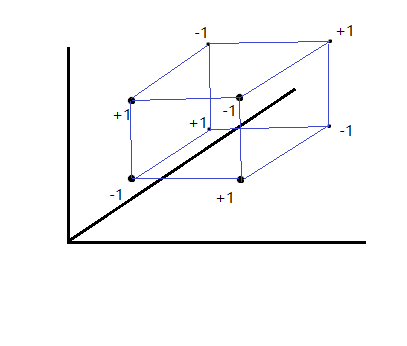
比如一次操作要对图中八个点形成的立体区间的所有值$-1$，那每个角点的差分值变化就是点旁标的数字。

其实，我们会发现一个规律，就是相邻的两个点的差分值一定是相反的。

原因很简单：由于是区间运算，不管在哪一维度，只要前面有一个点的差分值增大或减小，后面就一定有一个点把差分值补回去，这样才能保证不修改到区间后的数。

所以可以用类似二分图匹配的方法计算多维差分时，操作空间的每个顶点的差分值的正负。这里只有三维，所以可以直接赋。

三维差分计算每个位置的当前数的方法：递推求以 $(0,0,0)$ 为左下角，当前点为右上角的立方体中所有位置的差分和。

这样的时间复杂度是$O(维度*空间大小)$的，对于本题就是$O(3*ABC)$。

以上是用$O(m)$的时间求出$m$次操作后所有飞船剩余的血量的方法。这种方法只能快速求出一定次操作后的差分值，对于不同的操作次数，得到每个位置的数所需的时间复杂度很高（得暴力跑一遍$A*B*C$的矩阵），所以不能过多次得到整个矩阵当前每个位置的数（暴力是能的）。因此套用二分就得到了与暴力不同的高效做法。

总结一下，就是对于前$m$个操作，每个操作都修改8个位置的差分值，都操作完后多维差分计算每个位置的数，最后暴力判断每个数是否$\lt 0$ 即可。（只要找到一个就可以退出$check$）

外面套二分，时间复杂度$O(log(m)*(m+ABC))$。

时间复杂度如何优化到理论$O(m+ABC)$

首先，我们的二分有特殊性质，即相邻两次二分的答案的变化量依次为 $\frac{m}{2},\frac{m}{4},\frac{m}{8}$，以此类推。

图中的蓝色编号为二分答案顺序，下面的彩色细线为移动长度。

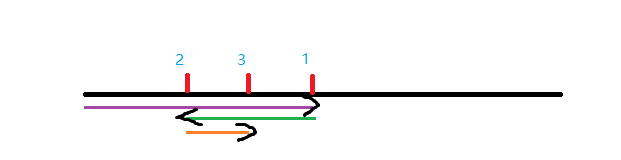
由于这题比较特殊，二分的是攻击次数，所以我们不必每次二分都重新差分前面的攻击操作，造成大量重复计算，而直接在原差分值的基础上修改二分答案的变化量次即可。

根据调和级数，这样的总差分次数是 $\frac{m}{2}+\frac{m}{4}+\frac{m}{8}+...\le 1$，所有差分修改的总时间复杂度就变成了$O(m)$。

如果你不理解调和级数，我这里有个通俗易懂的解释能证明调和级数：把上式结果转为二进制，由于每个加数都把互不相同的一位都加了$1$，表示出来就是$0.1111...$（小数位可以有任意多个$1$），可以看出它无限接近但不等于$1$。

这个优化是可以实际操作的，于是时间复杂度变成了$O(m+log(m)*ABC)$。

那$ABC$呢？

可以再考虑一下这题的特征：任意飞船血量是单调不上升的。

这就说明，对于二分出的一个攻击次数$m$，如果存在血量$\lt 0$ 的飞船，我们肯定要降低答案的二分范围，而此时那些血量$\ge 0$ 的飞船在减少被攻击次数后血量肯定还$\ge 0$，依然不可能成为答案，所以我们可以用链表存储飞船矩阵，然后在上述情况时删掉这些位置。

但实际上三维链表很难写，所以最多记个$vis$数组记录被删掉的位置。

而且这个优化仅限于理论，实际上它的优化效果是不定的，时间复杂度最优是$O(m+ABC)$，最坏还是$O(m+log(m)*ABC)$（正好要进行完$m$次攻击后才能出现一个挂掉的飞船时，上述优化就没法用）。

代码是$syf$大佬的 $AC\space code$，格式嘛……

 #include<bits/stdc++.h>
 #define rep(i,x,y) for(register int i=(x);i<=(y);i++)
 #define dwn(i,x,y) for(register int i=(x);i>=(y);i--)
 #define maxn 1000010
 #define LL long long
 using namespace std;
 int read()
 {
     int x=,f=;char ch=getchar();
     while(!isdigit(ch)&&ch!='-')ch=getchar();
     if(ch=='-')f=-,ch=getchar();
     while(isdigit(ch))x=(x<<)+(x<<)+ch-'',ch=getchar();
     return x*f;
 }
 void write(int x)
 {
     int f=;char ch[];
     if(!x){putchar(''),putchar('\n');return;}
     if(x<)x=-x,putchar('-');
     while(x)ch[++f]=x%+'',x/=;
     while(f)putchar(ch[f--]);
     putchar('\n');
 }
 LL qh[maxn],a[maxn],s[maxn],d[maxn];
 int qxa[maxn],qya[maxn],qza[maxn],qxb[maxn],qyb[maxn],qzb[maxn],A,B,C,m,ans;
 int getx(int x,int y,int z){return (x*B+y)*C+z+;}
 void getp(int x,int px,int py,int pz){x--;pz=x%C,x/=C,py=x%B,pz=x/B;return;}
 void add(int x,int y,int z,LL h){if(x<=(A-)&&y<=(B-)&&z<=(C-))a[getx(x,y,z)]+=h;}
 void atk(int xa,int ya,int za,int xb,int yb,int zb,LL h)
 {
     add(xa,ya,za,h),add(xa,ya,zb+,-h),add(xa,yb+,za,-h),add(xa,yb+,zb+,h);
     add(xb+,ya,za,-h),add(xb+,ya,zb+,h),add(xb+,yb+,za,h),add(xb+,yb+,zb+,-h);
 }
 int check()
 {
     rep(i,,A-)rep(j,,B-)rep(k,,C-)s[getx(i,j,k)]=a[getx(i,j,k)];
     if(C!=)rep(i,,A-)rep(j,,B-)rep(k,,C-)s[getx(i,j,k)]+=s[getx(i,j,k-)];//,cout<<i<<" "<<j<<" "<<k<<"+1 "<<s[getx(i,j,k-1)]<<endl;
     if(B!=)rep(i,,A-)rep(j,,B-)rep(k,,C-)s[getx(i,j,k)]+=s[getx(i,j-,k)];//,cout<<i<<" "<<j<<" "<<k<<"+2 "<<s[getx(i,j-1,k)]<<endl;
     if(A!=)rep(i,,A-)rep(j,,B-)rep(k,,C-)s[getx(i,j,k)]+=s[getx(i-,j,k)];//,cout<<<<"+3 "<<s[getx(i-1,j,k)]<<endl;
     rep(i,,A-)rep(j,,B-)rep(k,,C-)if(s[getx(i,j,k)]>d[getx(i,j,k)])return ;
     return ;
 }
 void getans(int L,int R,int lastmid)
 {
     if(L>R)return;
     int mid=(L+R)>>;
     if(mid>lastmid)rep(i,lastmid+,mid)/*cout<<"mid:"<<mid<<" add:"<<i<<endl,*/atk(qxa[i],qya[i],qza[i],qxb[i],qyb[i],qzb[i],qh[i]);
     if(mid<lastmid)rep(i,mid+,lastmid)/*cout<<"mid:"<<mid<<" del:"<<i<<endl,*/atk(qxa[i],qya[i],qza[i],qxb[i],qyb[i],qzb[i],-qh[i]);
     int f=check();
     //cout<<"mid:"<<mid;
     //cout<<"now:";
     //rep(i,0,A-1)rep(j,0,B-1)rep(k,0,C-1)cout<<s[getx(i,j,k)]<<" ";cout<<endl;
     if(f){ans=min(ans,mid);getans(L,mid-,mid);}
     else getans(mid+,R,mid);
 }
 int main()
 {
     //freopen("attack.in","r",stdin);
     //freopen("attack.out","w",stdout);
     A=read(),B=read(),C=read(),ans=m=read();
     rep(i,,A-)rep(j,,B-)rep(k,,C-)d[getx(i,j,k)]=read();
     rep(i,,m)qxa[i]=read()-,qxb[i]=read()-,qya[i]=read()-,qyb[i]=read()-,qza[i]=read()-,qzb[i]=read()-,qh[i]=read();
     getans(,m,);
     write(ans);
     return ;
 }
 /*
 2 2 2 3
 1 1 1 1 1 1 1 1
 1 2 1 2 1 1 1
 1 1 1 2 1 2 1
 1 1 1 1 1 1 2
 */