C语言8大经典排序算法（2）

二、插入类排序

　插入排序(Insertion Sort)的基本思想是：每次将一个待排序的记录，按其关键字大小插入到前面已经排好序的子文件中的适当位置，直到全部记录插入完成为止。

插入排序一般意义上有两种：直接插入排序和希尔排序，下面分别介绍。

3、直接插入排序

基本思想：

最基本的操作是将第i个记录插入到前面i-1个以排好序列的记录中。具体过程是：将第i个记录的关键字K依次与其前面的i-1个已经拍好序列的记录进行比较。将所有大于K的记录依次向后移动一个位置，直到遇到一个关键字小于或等于K的记录，此时它后面的位置必定为空，则将K插入。

图示：

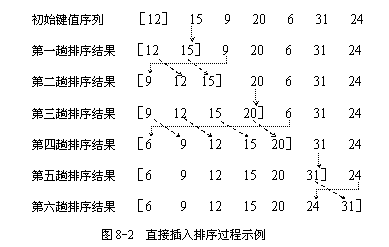
C语言实现：（直接把后面小的数插入到前面对应位置）

void Insertsort1(int a[], int n)
{
    int i, j, k;
    for (i = ; i < n; i++)
    {
        //为a[i]在前面的a[0...i-1]有序区间中找一个合适的位置
        for (j = i - ; j >= ; j--)
            if (a[j] < a[i])
                break;  

        //如找到了一个合适的位置
        if (j != i - )
        {
            //将比a[i]大的数据向后移
            int temp = a[i];
            for (k = i - ; k > j; k--)
                a[k + ] = a[k];
            //将a[i]放到正确位置上
            a[k + ] = temp;
        }
    }
}

算法分析：

1．算法的时间性能分析

我们来分析一下这个算法，从空间上来看，它只需要一个记录的辅助空间，因此关键是看它的时间复杂度。

当最好的情况，也就是要排序的表本身就是有序的，比如纸牌拿到后就是{2,3,4,5,6}，那么我们比较次数，其实就是代码第6行每个L.r[i]与L.r[i‐1]的比较，共比较了次，由于每次都是L.r[i]>L.r[i‐1]，因此没有移动的记录，时间复杂度为O(n)。

当最坏的情况，即待排序表是逆序的情况，比如{6,5,4,3,2}，此时需要比较 次，而记录的移动次数也达到最大值 次。

如果排序记录是随机的，那么根据概率相同的原则，平均比较和移动次约为   次。因此，我们得出直接插入排序法的时间复杂度为O(n2)。从这里也看出，同样的O(n2)时间复杂度，直接插入排序法比冒泡和简单选择排序的性能要好一些。

2．直接插入排序的稳定性
　直接插入排序是稳定的排序方法。

直接插入排序法，针对少量的数据项排序，速度比较快，数据越大，这中方法的劣势也就越明显了。

改进方案：折半插入排序（binary insertion sort）

思路：折半插入排序（binary insertion sort）是对插入排序算法的一种改进，由于排序算法过程中，就是不断的依次将元素插入前面已排好序的序列中。由于前半部分为已排好序的数列，这样我们不用按顺序依次寻找插入点，可以采用折半查找的方法来加快寻找插入点的速度。

具体操作：在将一个新元素插入已排好序的数组的过程中，寻找插入点时，将待插入区域的首元素设置为a[low],末元素设置为a[high]，则轮比较时将待插入元素与a[m],其中m=(low+high)/2相比较,如果比参考元素小，则选择a[low]到a[m-1]为新的插入区域(即high=m-1)，否则选择a[m+1]到a[high]为新的插入区域（即low=m+1），如此直至low<=high不成立，即将此位置之后所有元素后移一位，并将新元素插入a[high+1]。

C语言实现：

 void BInsertSort(int data[],int n)
  {
       int low,high,mid;
       int temp,i,j;
       for(i=1;i<n;i++)
       {
                       low=0;
                       temp=data[i];// 保存要插入的元素
                      high=i-1;
                    while(low<=high) //折半查找到要插入的位置
                    {
                   mid=(low+high)/2;
                      if(data[mid]>temp)
                         high=mid-1;
                      else
                       low=mid+1;
                     }
                int j = i;
            while ((j > low) && (arr[j - 1] > t))
            {
                arr[j] = arr[j - 1];//交换顺序
                --j;
            }
            arr[low] = temp;  

 } 

 }

算法分析：折半插入排序算法是一种稳定的排序算法，比直接插入算法明显减少了关键字之间比较的次数，因此速度比直接插入排序算法快，但记录移动的次数没有变，所以折半插入排序算法的时间复杂度仍然为O(n^2)，与直接插入排序算法相同。附加空间O(1)。

4、希尔排序

希尔排序(Shell Sort)是插入排序的一种。是针对直接插入排序算法的改进。该方法又称缩小增量排序，因DL．Shell于1959年提出而得名。

基本思想：
　    先取一个小于n的整数d₁作为第一个增量，把文件的全部记录分成d₁个组。所有距离为d_l的倍数的记录放在同一个组中。先在各组内进行直接插人排序；然后，取第二个增量d₂<d₁重复上述的分组和排序，直至所取的增量d_t=1(d_t<d_t-l<…<d₂<d₁)，即所有记录放在同一组中进行直接插入排序为止。
    　该方法实质上是一种分组插入方法。

举例阐述：

例如，假设有这样一组数[ 13 14 94 33 82 25 59 94 65 23 45 27 73 25 39 10 ]，如果我们以步长为5开始进行排序，我们可以通过将这列表放在有5列的表中来更好地描述算法，这样他们就应该看起来是这样：

13 14 94 33 82
25 59 94 65 23
45 27 73 25 39
10

然后我们对每列进行排序：

10 14 73 25 23
13 27 94 33 39
25 59 94 65 82
45

将上述四行数字，依序接在一起时我们得到：[ 10 14 73 25 23 13 27 94 33 39 25 59 94 65 82 45 ].这时10已经移至正确位置了，然后再以3为步长进行排序：

10 14 73
25 23 13
27 94 33
39 25 59
94 65 82
45

排序之后变为：

10 14 13
25 23 33
27 25 59
39 65 73
45 94 82
94

最后以1步长进行排序（此时就是简单的插入排序了）。

图示：

C++代码实现：

 1 void shellsort(int *data, size_t size)
 2 {
 3     for (int gap = size / 2; gap > 0; gap /= 2)
 4         for (int i = gap; i < size; ++i)
 5         {
 6
 7              int key = data[i];
 8              int j = 0;
 9              for( j = i -gap; j >= 0 && data[j] > key; j -=gap)
10              {
11                 data[j+gap] = data[j];
12               }
13              data[j+gap] = key;
14          }
15 }

性能分析：

希尔排序是按照不同步长对元素进行插入排序，当刚开始元素很无序的时候，步长最大，所以插入排序的元素个数很少，速度很快；当元素基本有序了，步长很小，插入排序对于有序的序列效率很高。所以，希尔排序的时间复杂度会比o(n^2)好一些。由于多次插入排序，我们知道一次插入排序是稳定的，不会改变相同元素的相对顺序，但在不同的插入排序过程中，相同的元素可能在各自的插入排序中移动，最后其稳定性就会被打乱，所以shell排序是不稳定的。

最差时间复杂度	根据步长序列的不同而不同。 已知最好的:
最优时间复杂度	O(n)
平均时间复杂度	根据步长序列的不同而不同。