1.1.1最短路（Floyd、Dijstra、BellmanFord）

转载自hr_whisper大佬的博客

[

一、Dijkstra

比较详细的迪杰斯特拉算法讲解传送门

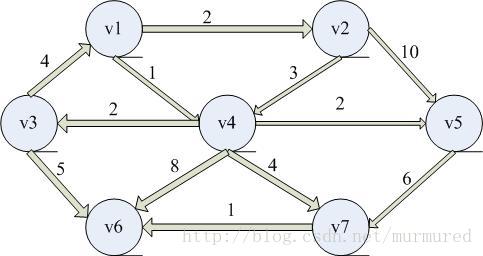
Dijkstra单源最短路算法，即计算从起点出发到每个点的最短路。所以Dijkstra常常作为其他算法的预处理。

使用邻接矩阵的时间复杂度为O(n^2),用优先队列的复杂度为O((m+n)logn)近似为O(mlogn)

(一) 过程

每次选择一个未访问过的到已经访问过（标记为Known）的所有点的集合的最短边，并用这个点进行更新，过程如下：

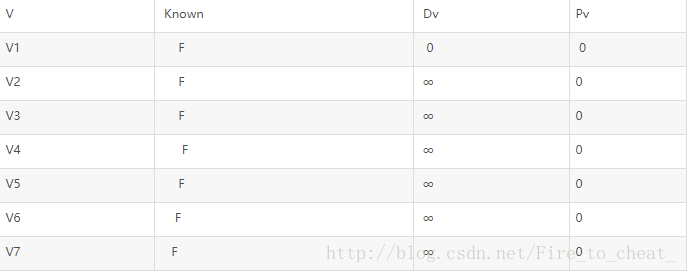
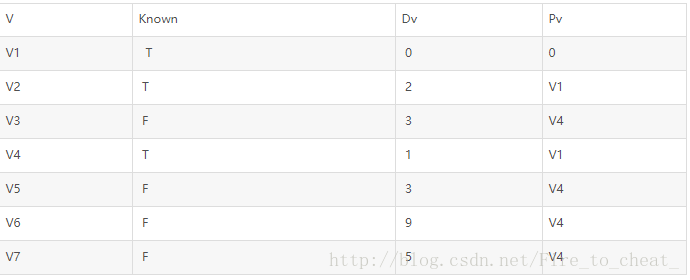
Dv为最短路，而Pv为前面的顶点。

初始
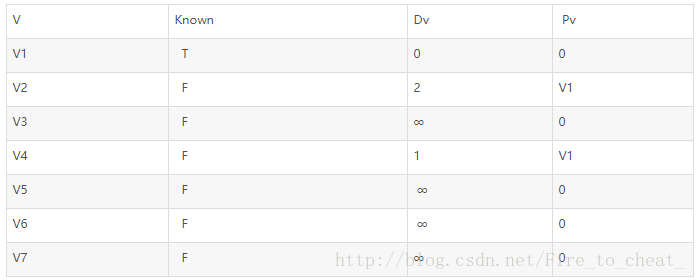
在v1被标记为已知后的表
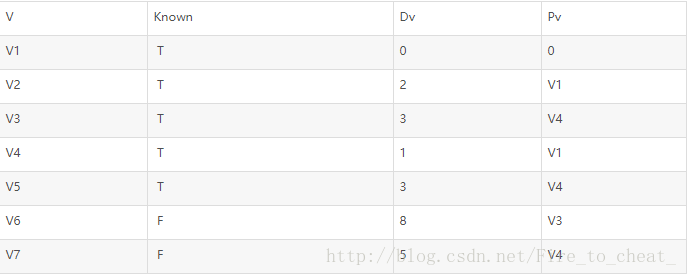
下一步选取v4并且标记为known，顶点v3,v5,v6,v7是邻接的顶点，而他们实际上都需要调整。如表所示:
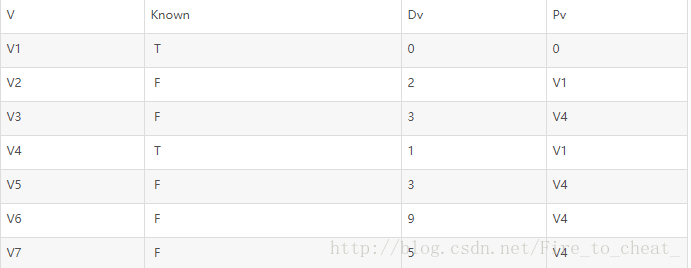
接下来选取v2,v4是邻接点，但已经是known的，不需要调整，v5是邻接的点但不做调整，因为经过v2的值为2+10=12而长为3的路径已经是已知的。
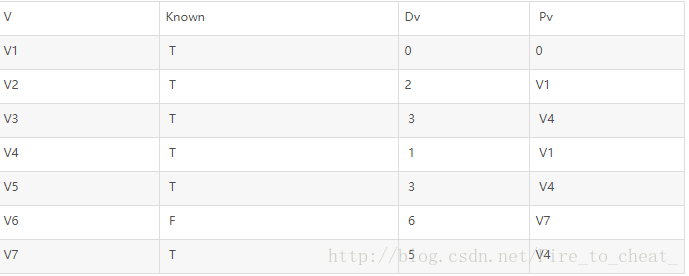
接下来选取v5，值为3，v7 3+6>5不需调整，然后选取v3，对v6的距离下调到3+5=8
再选下一个顶点是v7，v6变为5+1=6
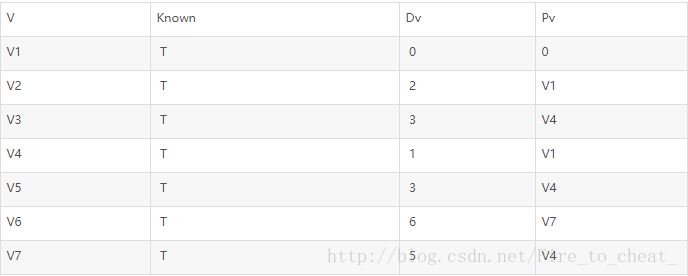
最后选取v6

(二) 局限性

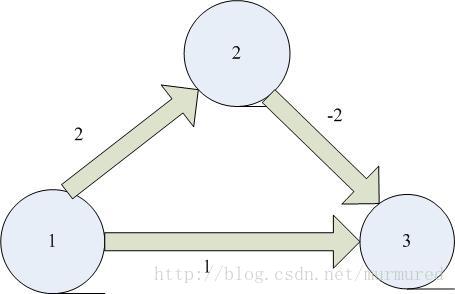
Dijkstra没办法解决负边权的最短路径，如图

运行完该算法后，从顶点1到顶点3的最短路径为1,3，其长度为1，而实际上最短路径为1,2,3，其长度为0.（因为过程中先选择v3，v3被标记为已知，今后不再更新）

(三) 算法实现。

1．普通的邻接表以（HDU 1874 畅通工程续 SPFA || dijkstra）为例

用vis作为上面标记的known，dis记录最短距离（记得初始化为一个很大的数）。

（1）Dijkstra+邻接矩阵

#include<cstdio>

#include<cstring>

const int MAXN=200+10;

const int INF=1000000;

int n,m,map[MAXN][MAXN],dis[MAXN];

bool vis[MAXN];

void dijkstra(int s)

{

    memset(vis,0,sizeof(vis));

    int cur=s;

    dis[cur]=0;

    vis[cur]=1;

    for(int i=0;i<n;i++)

    {

        for(int j=0;j<n;j++)

            if(!vis[j] && dis[cur] + map[cur][j] < dis[j])

                dis[j]=dis[cur] + map[cur][j] ;

        int mini=INF;

        for(int j=0;j<n;j++)

            if(!vis[j] && dis[j] < mini)

                mini=dis[cur=j];

        vis[cur]=true;

    }

}

int main()

{

    while(~scanf("%d%d",&n,&m))

    {

        for(int i=0;i<n;i++)

        {

            dis[i]=INF;

            for(int j=0;j<n;j++)

                map[i][j]=INF;

        }

        for(int i=0;i<m;i++)

        {

            int from,to,val;

            scanf("%d%d%d",&from,&to,&val);

            if(map[from][to] > val)

                map[to][from]=map[from][to]=val;

        }

        int s,t;

        scanf("%d%d",&s,&t);

        dijkstra(s);

        if(dis[t]==INF)

            printf("-1\n");

        else

            printf("%d\n",dis[t]);

    }

    return 0;

}

（2）Dijkstra+优先队列

#include<cstdio>

#include<cstring>

#include<queue>

using namespace std;

const int MAXN=200+10;

const int MAXM=40000+10;

const int INF=1000000;

int n,m,dis[MAXN],head[MAXN],len;

bool vis[MAXN];

struct edge

{

    int to,val,next;

}e[MAXM];

void add(int from,int to,int  val)

{

    e[len].to=to;

    e[len].val=val;

    e[len].next=head[from];

    head[from]=len++;

}

struct point

{

    int val,id;

    point(int id,int val):id(id),val(val){}

    bool operator <(const point &x)const{

        return val>x.val;

    }

};

void dijkstra(int s)

{

    memset(vis,0,sizeof(vis));

    for(int i=0;i<n;i++)

        dis[i]=INF; 

    priority_queue<point> q;

    q.push(point(s,0));

    dis[s]=0;

    while(!q.empty())

    {

        int cur=q.top().id;

        q.pop();

        if(vis[cur]) continue;

        vis[cur]=true;

        for(int i=head[cur];i!=-1;i=e[i].next)

        {

            int id=e[i].to;

            if(!vis[id] && dis[cur]+e[i].val < dis[id])

            {

                dis[id]=dis[cur]+e[i].val;

                q.push(point(id,dis[id]));

            }

        }

    }

}

int main()

{

    while(~scanf("%d%d",&n,&m))

    {

        len=0;

        memset(head,-1,sizeof(head));

        for(int i=0;i<m;i++)

        {

            int from,to,val;

            scanf("%d%d%d",&from,&to,&val);

            add(from,to,val);

            add(to,from,val);

        }

        int s,t;

        scanf("%d%d",&s,&t);

        dijkstra(s);

        if(dis[t]==INF)

            printf("-1\n");

        else

            printf("%d\n",dis[t]);

    }

    return 0;

}

二、SPFA（bellman-ford）

（一）原理过程

关于SPFA算法详细介绍传送门

（二）实现

1.邻接矩阵的SPFA以（HDU 1874 畅通工程续 SPFA || dijkstra）为例：

#include<cstdio>

#include<queue>

using namespace std;

const int INF=1000000;

const int MAXN=200+10;

int n,m;

int map[MAXN][MAXN];

int dis[MAXN];

void SPFA(int s)

{

    for(int i=0;i<n;i++)

        dis[i]=INF;

    bool vis[MAXN]={0};

    vis[s]=true;

    dis[s]=0;

    queue<int> q;

    q.push(s);

    while(!q.empty())

    {

        int cur=q.front();

        q.pop();

        vis[cur]=false;

        for(int i=0;i<n;i++)

        {

            if(dis[cur] + map[cur][i] < dis[i])

            {

                dis[i]=dis[cur] + map[cur][i];

                if(!vis[i])

                {

                    q.push(i);

                    vis[i]=true;

                }

            }

        }

    }

}

int main()

{

    while(~scanf("%d%d",&n,&m))

    {

        for(int i=0;i<n;i++)

            for(int j=0;j<n;j++)

                map[i][j]=INF;

        for(int i=0;i<m;i++)

        {

            int from,to,dis;

            scanf("%d%d%d",&from,&to,&dis);

            if(map[from][to]>dis)

                map[from][to]=map[to][from]=dis;

        }

        int s,t;

        scanf("%d%d",&s,&t);

        SPFA(s);

        if(dis[t]==INF)

            puts("-1");

        else

            printf("%d\n",dis[t]);

    }

    return 0;

}

2.SPFA+邻接表

#include<cstdio>

#include<cstring>

#include<queue>

using namespace std;

const int MAXN=200+10;

const int MAXM=40000+10;

const int INF=1000000;

int n,m,dis[MAXN],head[MAXN],len;

bool vis[MAXN];

struct edge

{

    int to,val,next;

}e[MAXM];

void add(int from,int to,int  val)

{

    e[len].to=to;

    e[len].val=val;

    e[len].next=head[from];

    head[from]=len++;

}

void spfa(int s)

{

    memset(vis,0,sizeof(vis));

    for(int i=0;i<n;i++)

        dis[i]=INF;    

    queue<int> q;

    q.push(s);

    vis[s]=true;

    dis[s]=0;

    while(!q.empty())

    {

        int cur=q.front();

        q.pop();

        vis[cur]=false;

        for(int i=head[cur];i!=-1;i=e[i].next)

        {

            int id=e[i].to;

            if(dis[id] > dis[cur]+e[i].val)

            {

                dis[id] = dis[cur] + e[i].val;

                if(!vis[id])

                {

                    vis[id]=true;

                    q.push(id);

                }

            }

        }

    }

}

int main()

{

    while(~scanf("%d%d",&n,&m))

    {

        len=0;

        memset(head,-1,sizeof(head));

        for(int i=0;i<m;i++)

        {

            int from,to,val;

            scanf("%d%d%d",&from,&to,&val);

            add(from,to,val);

            add(to,from,val);

        }

        int s,t;

        scanf("%d%d",&s,&t);

        spfa(s);

        if(dis[t]==INF)

            printf("-1\n");

        else

            printf("%d\n",dis[t]);

    }

    return 0;

}

三、Floyd

全称Floyd-Warshall。记得离散数学里面有Warshall算法，用来计算传递闭包。而数据结构每次都简称floyd，当时就觉得两个都差不多，有神马关系，后来google一下发现是同一个算法。。。。改个名字出来走江湖啊！！！！！

这个算法用于求所有点对的最短距离。比调用n次dijkstra的优点在于代码简单。

（一）原理过程

这是一个dp（动态规划的过程）

dis[i][j]=min(dis[i][j],dis[i][k]+dis[k][j]);

即从顶点i到j且经过顶点k的最短路径长度。

（二）实现

以（HDU 1874 畅通工程续 SPFA || dijkstra）为例

#include<cstdio>

#include<cstring>

#include<algorithm>

using namespace std;

const int MAXN=200+10;

const int INF=1000000;

int n,m,dis[MAXN][MAXN];

void floyd()

{

    for(int k=0;k<n;k++)

        for(int i=0;i<n;i++)

            for(int j=0;j<n;j++)

                dis[i][j]=min(dis[i][j],dis[i][k]+dis[k][j]);

}

int main()

{

    while(~scanf("%d%d",&n,&m))

    {

        for(int i=0;i<n;i++)

            for(int j=0;j<n;j++)

              dis[i][j]=INF;

        for(int i=0;i<m;i++)

        {

            int from,to,val;

            scanf("%d%d%d",&from,&to,&val);

            if(dis[from][to] > val)

                dis[to][from]=dis[from][to]=val;

        }

        int s,t;

        scanf("%d%d",&s,&t);

        if(s==t)

        {

            printf("0\n");

            continue;

        }

        floyd();

        if(dis[s][t]==INF)

            printf("-1\n");

        else

            printf("%d\n",dis[s][t]);

    }

    return 0;

}

如走迷宫经常用的BFS，以一个点出发，向外扩散。

如：

UVA 10047 - TheMonocycle BFS

HDU 1728逃离迷宫 BFS

POJ3984迷宫问题 BFS

UVA 11624 - Fire!图BFS

除了上面的

HDU 1874畅通工程续 SPFA || dijkstra||floyd

还有：

UVA11280 - Flying to Fredericton SPFA变形

UVA11090 - Going in Cycle!! SPFA

UVA10917 Walk Through the Forest SPFA

POJ 3259Wormholes邻接表的SPFA判断负权回路

POJ 1932XYZZY (ZOJ 1935)SPFA+floyd

UVA11374 Airport Express SPFA||dijkstra

UVA11367 - Full Tank? dijkstra+DP

POJ 1511Invitation Cards (ZOJ 2008)使用优先队列的dijkstra

POJ 3268Silver Cow Party (Dijkstra~)

POJ 2387Til the Cows Come Home (Dijkstra)

UVA10603 - Fill BFS~