期望dp好题选做

前言：

最近连考两场期望dp的题目，sir说十分板子的题目我竟然一点也不会，而且讲过以后也觉得很不可改。于是开个坑。

1.晚测10 T2 大佬(kat)

明明有\(O(mlog)\)的写法，但是\(m\)等于\(500\)就让人十分迷惑。当然我并没有推出来

以下式子来自这里

emm，目前觉得DeepinC的式子最好理解，也最好写 其实我就看懂了一个

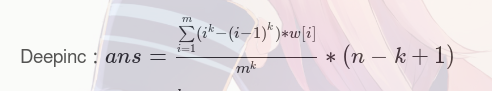
下面的\(m^k\)显然是总方案数，后面乘的\((n-k+1)\)提醒我们这个式子是在枚举每一个区间。

至于分子上的东西，

从\(1\)到\(m\)枚举当前区间造成贡献的数是多少。

假设当前枚举到\(i\)

那么方案数就是\(i^k-(i-1)^k\) ,前面是每个数值域在\([1,i]\)的方案数，后面是每个数值域在\([1,i-1]\)的方案数，相减就是这个区间内至少有一个是\(i\)的方案数。

然后乘以对应的\(w[i]\)，求个和。

实际意义大概就是这样的。

P.S.

那我为什么交了折磨多次68分呢？

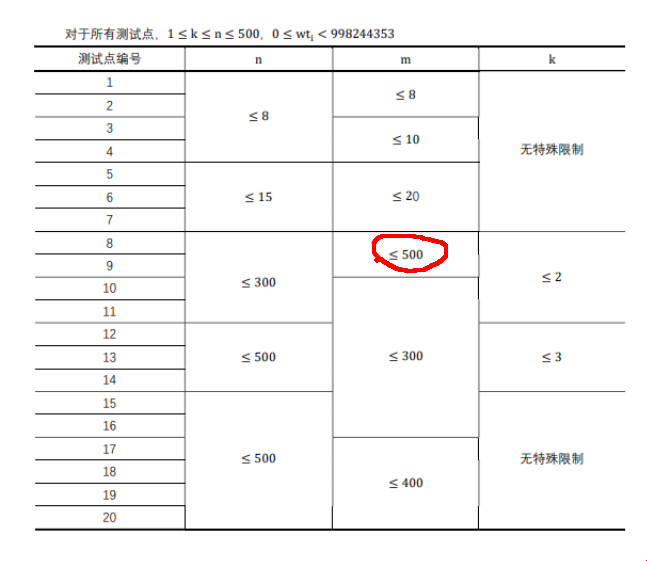
不会真的有人能看到m是500吧，不会吧不会吧不会吧

1.联考Day5 T2 客星璀璨之夜

貌似是HDU 6848的弱化版？

这个题可以\(O(n^2)\)解决掉。原题貌似就要\(O(nlog)\)了，我不会。

首先，这类题目的一个常用套路是，用每一个元素对答案的贡献，乘以每一个元素的贡献次数，求和再除以总方案数。

这个题里面，首先可以发现，每条路径出现的次数只与当前的点数和这条路径第一个点的位置有关。

所以我们用dp[i][j]表示，这条路径中间有i对点，右面有j对点的方案数（不考虑左面的方案数，当作左面是0个）。

考虑转移。

dp[i][j]=dp[i-1][j]*(i*2-1)+dp[i][j-1]*(j*2+1);

这里我们相当与枚举下一次是哪个点进行碰撞。中间有i对点，除了最右面的，其他点都可以向左或向右。右面的j对点同理。

当然，有：

\(dp[0][0]=1\)

\(dp[0][i]=dp[0][i-1]*(i*2-1)*i!*2^i\)

\(dp[i][0]=dp[i-1][0]*(i*2-1)\)

这里要说一下\(dp[0][i]\)和\(dp[i][0]\)转移的区别。

\(dp[i][0]\):右面没有点对。也就是说，我们选择作出贡献的点对必须在i对点碰撞完之后才能进行碰撞。

\(dp[0][i]\):中间没有点对，也就是说，我们选择作出贡献的点对可以在i对点碰撞的过程中进行碰撞，所以要乘以\((i!*2^i)\)

然后我们就求出了方案数（左面的方案没有乘）

现在只要枚举造成贡献的路径，再乘以对应的dp[i][j]，再乘以左面的方案数，再求个和，最后除以总方案数，就完了！

具体实现：第一维枚举奇数点，第二维枚举偶数点。如果x<y,就普通算，如果是x>y,就让x=2n+1-x+1,y=2n+1-y，相当与让整个序列反转，这样求方案数更加方便。

当然，如果这么敲上去，大概会拿到90分的好成绩，因为快速幂带个log，就很烦。

只要预处理一下就行了。

代码：

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=3000+10,maxm=6000+10,mod=998244353;
#define gc() (p1 == p2 ? (p2 = buf + fread(p1 = buf, 1, 1 << 20, stdin), p1 == p2 ? EOF : *p1++) : *p1++)
#define read() ({ register int x = 0, f = 1; register char c = gc(); while(c < '0' || c > '9') { if (c == '-') f = -1; c = gc();} while(c >= '0' && c <= '9') x = x * 10 + (c & 15), c = gc(); f * x; })
char buf[1 << 20], *p1, *p2;
int a[maxm];
ll dp[maxn][maxn];
ll fac[maxn],facn[maxn],n2[maxn];
int n;
ll ans;
ll qpow(ll x,int y){
	ll res=1;
	ll base=x;
	while(y){
		if(y&1) res=res*base%mod;
		base=base*base%mod;
		y>>=1;
	}
	return res;
}
void Solve(){
	scanf("%d",&n);
	fac[0]=1;
	for(register int i=1;i<=n;++i) fac[i]=fac[i-1]*i%mod;
	for(int i=1;i<=n;++i) facn[i]=qpow(fac[i],mod-2);
	n2[0]=1;
	for(int i=1;i<=n;++i) n2[i]=qpow(2,i);
	for(register int i=1;i<=(n<<1)+1;++i) scanf("%d",&a[i]);
	dp[0][0]=1;
	for(register int i=1;i<=n;++i){
		dp[i][0]=dp[i-1][0]*(i*2-1)%mod;
		dp[0][i]=(dp[0][i-1]*(i*2-1)%mod+fac[i]%mod*qpow(2,i)%mod)%mod;
	}
	for(register int i=1;i<=n;++i){
		for(register int j=1;j<=n;++j){
			dp[i][j]=(dp[i-1][j]*(i*2-1)+dp[i][j-1]*(j*2-1))%mod;
		}
	}
	for(register int i=2;i<=(n*2);i+=2){
		for(register int j=1;j<=n*2+1;j+=2){
			int x=i;
			int y=j;
			if(x>y) x=2*n+1-x+1,y=2*n+1-y;
			ans=(ans+1ll*abs(a[i]-a[j])*dp[(y-x)/2][(n*2+1-y)/2]%mod*n2[(x-2)/2]%mod*fac[n]%mod*facn[n-(x-2)/2])%mod;
			//ans=(ans+1ll*abs(a[i]-a[j])*dp[(y-x)/2][(n*2+1-y)/2]%mod*qpow(2,(x-2)/2)%mod*fac[n]%mod*qpow((fac[n-(x-2)/2]),mod-2))%mod;
		}
	}
	ans=ans*qpow(qpow(2,n)*fac[n]%mod,mod-2)%mod;
	printf("%lld\n",ans);
}
int main(){
	//freopen("stars.in","r",stdin);
	//freopen("stars.out","w",stdout);
	Solve();
	return 0;
}