Atcoder Grand Contest 032 E - Modulo Pairing（乱搞+二分）

Atcoder 题面传送门 & 洛谷题面传送门

神仙调整+乱搞题。

首先某些人（including me）一看到最大值最小就二分答案，事实上二分答案对这题正解没有任何启发。

首先将 \(a_i\) 从小到大排序。我们考虑将分配的点对看作一条条线，对于 \(a_x+a_y<M\) 的点对 \((x,y)\) 我们在 \(x,y\) 之间连一条蓝线，对于 \(a_x+a_y\ge M\) 的点对我们在 \(x,y\) 之间连一条红线。

先抛结论，再给证明：如在最优分配方式中，我们的连线方式肯定是长这样的：

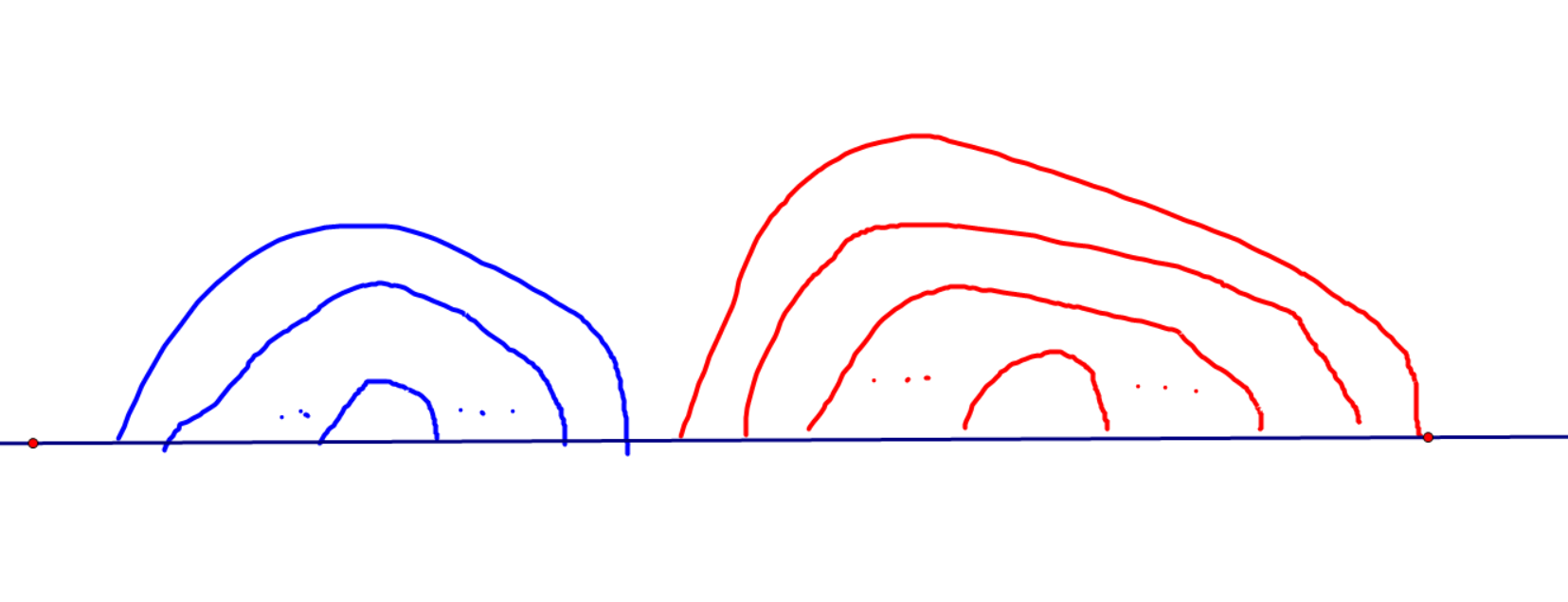
证明：使用调整法，证明上述命题，等价于证明对于以下 \(7\) 种情况，左边的情况都可以被调整为右边的情况且答案不会更劣（这里借用了粉兔题解中的图）：

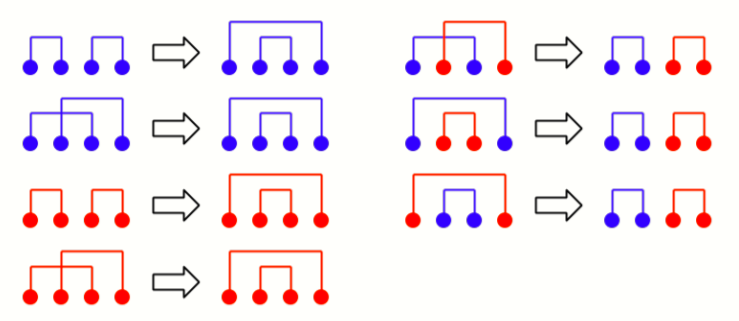
我们考虑一一对其进行证明，为了表述方便我们统一假设从左到右四个点分别为 \(a_p,a_q,a_r,a_s\)，则显然 \(a_p\le a_q\le a_r\le a_s\)：

1. 对于左边第一个的情况，左边的最大值为 \(\max(a_p+a_q,a_r+a_s)=a_r+a_s\)，右边的最大值为 \(\max(a_p+a_s,a_q+a_r)\)，而由于 \(a_p+a_s\le a_r+a_s,a_q+a_r\le a_r+a_s\)，故右边答案不会比左边更劣。
2. 对于右边第一个的情况，左边的最大值为 \(\max(a_p+a_r,a_q+a_s-M)\)，而由于 \(a_s-M<0\)，故 \(a_q+a_s-M<a_q<a_p+a_r\)，故左边的最大值实际上是 \(a_p+a_r\)，右边的最大值为 \(\max(a_p+a_q,a_r+a_s-M)\)，而显然 \(a_p+a_q\le a_p+a_r,a_r+a_s-M<a_r\le a_p+a_r\)，故右边答案不会比左边更劣，同时又因为 \(a_p+a_q\le a_p+a_r<M,a_r+a_s\ge a_q+a_s\ge M\)，故 \(a_p,a_q\) 之间连的依旧是蓝线，\(a_r,a_s\) 之间连的依旧是红线。
3. 对于左边第二个的情况，左边的最大值为 \(a_q+a_s\)，右边的最大值为 \(\max(a_p+a_s,a_q+a_r)\)，而 \(a_p+a_s\le a_q+a_s,a_q+a_r\le a_q+a_s\)，故右边答案不会比左边更劣。
4. 对于右边第二个的情况，左边的最大值为 \(\max(a_p+a_s,a_q+a_r-M)=a_p+a_s\)，右边的最大值为 \(\max(a_p+a_q,a_r+a_s-M)\)，又由于 \(a_p+a_q\le a_p+a_s,a_r+a_s-M<a_r\le a_p+a_s\)，故右边答案不会比左边更劣。
5. 对于左边第三、四个的情况，证明方法同左边第一、二个，只不过需要整体减个 \(M\)。
6. 对于右边第三个的情况，左边最大值为 \(\max(a_q+a_r,a_p+a_s-M)=a_q+a_r\)，右边最大值为 \(\max(a_p+a_q,a_r+a_s-M)\)，又由于 \(a_p+a_q\le a_q+a_r,a_r+a_s-M<a_r\le a_q+a_r\)，故右边答案不会比左边更劣。

综上，只要出现线相交或者不同颜色的线出现包含关系的情况，都可以被调整，证毕。

接下来考虑怎样求答案，暴力枚举分割点显然是不可行的，不过注意到对于两个不同且均合法的分割点 \(p\) 和 \(p'\)，如果 \(p<p'\)，那么以 \(p\) 为分割点的每条线的权值都小于以 \(p'\) 为分割点的每条线的权值，因此我们肯定希望分割点越靠左越好，而如果我们分割点太左了（yyq：政治学得很好嘛），那就会出现右侧有的线不是红线的情况，因此我们可以二分找出合法的且最靠左的分割点 \(p\)，然后求出答案即可。

时间复杂度线性对数。

namespace fastio{
	#define FILE_SIZE 1<<23
	char rbuf[FILE_SIZE],*p1=rbuf,*p2=rbuf,wbuf[FILE_SIZE],*p3=wbuf;
	inline char getc(){return p1==p2&&(p2=(p1=rbuf)+fread(rbuf,1,FILE_SIZE,stdin),p1==p2)?-1:*p1++;}
	inline void putc(char x){(*p3++=x);}
	template<typename T> void read(T &x){
		x=0;char c=getchar();T neg=0;
		while(!isdigit(c)) neg|=!(c^'-'),c=getchar();
		while(isdigit(c)) x=(x<<3)+(x<<1)+(c^48),c=getchar();
		if(neg) x=(~x)+1;
	}
	template<typename T> void recursive_print(T x){if(!x) return;recursive_print(x/10);putc(x%10^48);}
	template<typename T> void print(T x){if(!x) putc('0');if(x<0) putc('-'),x=~x+1;recursive_print(x);}
	template<typename T> void print(T x,char c){if(!x) putc('0');if(x<0) putc('-'),x=~x+1;recursive_print(x);putc(c);}
	void print_final(){fwrite(wbuf,1,p3-wbuf,stdout);}
}
using namespace fastio;
const int MAXN=1e5;
int n,m,a[MAXN*2+5];
int add(int x,int y){return (x+y<m)?(x+y):(x+y-m);}
bool check(int mid){bool flg=1;for(int i=(mid<<1)+1;i<=n<<1;i++) flg&=(a[i]+a[(n<<1)+(mid<<1)+1-i]>=m);return flg;}
int main(){
	read(n);read(m);
	for(int i=1;i<=n<<1;i++) read(a[i]);
	sort(a+1,a+(n<<1)+1);int l=0,r=n,p=-1;
	while(l<=r){
		int mid=l+r>>1;
		if(check(mid)) p=mid,r=mid-1;
		else l=mid+1;
	} int mx=0;
//	printf("%d\n",p);
	for(int i=1;i<=p<<1;i++) chkmax(mx,add(a[i],a[(p<<1)+1-i]));
	for(int i=(p<<1)+1;i<=n<<1;i++) chkmax(mx,add(a[i],a[(n<<1)+(p<<1)+1-i]));
	printf("%d\n",mx);
	return 0;
}