【数据结构与算法Python版学习笔记】算法分析
什么是算法分析
- 算法是问题解决的通用的分步的指令的聚合
- 算法分析主要就是从计算资源的消耗的角度来评判和比较算法。
计算资源指标
- 存储空间或内存
- 执行时间
影响算法运行时间的其他因素
- 分为最好、最差和平均情况,平均状况体现主流性能
累计求和案例
import timedef sumOFN2(n):start=time.time()theSum=0for i in range(1,n+1):theSum+=iend=time.time()return theSum,end-startdef sumOFN3(n):start=time.time()theSum=(n*(n+1))/2end=time.time()return theSum,end-startif __name__ == "__main__":for i in range(5):print("sum is %d required %10.7f seconds" % sumOFN2(100000))print("--------")for i in range(5):print("sum is %d required %10.7f seconds" % sumOFN3(100000))-----------sum is 5000050000 required 0.1255534 secondssum is 5000050000 required 0.1245010 secondssum is 5000050000 required 0.1389964 secondssum is 5000050000 required 0.1279476 secondssum is 5000050000 required 0.1276410 seconds--------sum is 5000050000 required 0.0000000 secondssum is 5000050000 required 0.0000000 secondssum is 5000050000 required 0.0000000 secondssum is 5000050000 required 0.0000000 secondssum is 5000050000 required 0.0000000 seconds
“大O” 表示法
数量级函数用来描述当规模 n 增加时, T(n)函数中增长最快的部分。
常见大O表示法
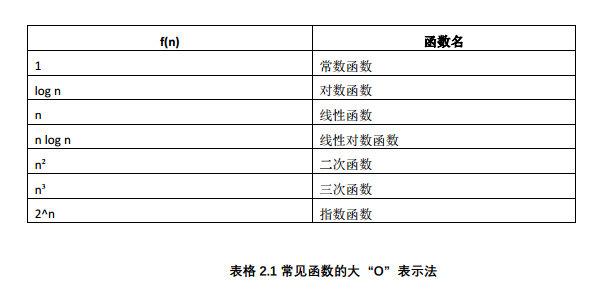
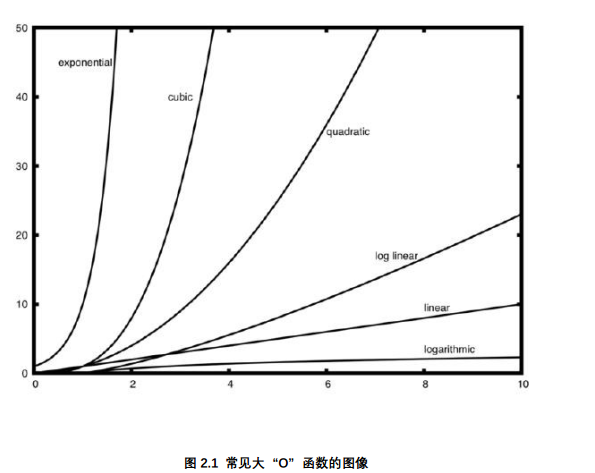
变 位 词 检 测
如果一个字符串是另一个字符串的重新排列组合,那么这两个字符串互为变位词。比如, ”heart”与”earth”互为变位词, ”python”与”typhon”也互为变位词。
- 逐字检查法 O(n²)
- 排序比较法 O(nlogn)
- 暴力匹配算法 O(n!)
- 字母计数比较法 O(n)
#变位词判断问题#逐字检查def anagramSolution(s1,s2):alist=list(s2)pos1=0stillOK=Truewhile pos1<len(s1) and stillOK:#循环s1中的每一个字符pos2=0found=Falsewhile pos2<len(alist) and not found:if s1[pos1]==alist[pos2]:found=Trueelse:pos2=pos2+1if found:alist[pos2]=Noneelse:stillOK=Falsepos1=pos1+1return stillOK#print(anagramSolution('abcd','dcba'))#排序解法def anagramSolution2(s1,s2):alist1=list(s1)alist2=list(s2)alist1.sort()alist2.sort()pos=0matches=Truewhile pos<len(s1) and matches:if alist1[pos]==alist2[pos]:pos=pos+1else:matches=Falsereturn matchesprint(anagramSolution2('abcd','dcba'))#计数器解法def anagramSolution3(s1,s2):c1=[0]*26c2=[0]*26for i in range(len(s1)):pos=ord(s1[i])-ord('a')#把a-z转化为0-25 ps:感谢m0_47550366的提醒,此处错误已改正c1[pos]=c1[pos]+1#计数for i in range(len(s2)):pos = ord(s2[i]) - ord('a') # 把a-z转化为0-25c2[pos] = c2[pos] + 1 # 计数j=0stillOK=Truewhile j<26 and stillOK:if c1[j]==c2[j]:j=j+1else:stillOK=Falsereturn stillOKprint(anagramSolution3('abcd','dcba'))
python数据类型
List 列表
```pythonimport timeit # 运行时间测量模块from timeit import Timer# 循环连接def test1():l=[]for i in range(1000):l=l+[i]# append添加def test2():l=[]for i in range(1000):l.append(i)# 列表推导式def test3():l=[i for i in range(1000)]# range转列表def test4():l=list(range(1000))if __name__ == "__main__":t1=Timer("test1()","from __main__ import test1")print("concat %f second" % t1.timeit(number=1000)) # number指定程序被执行的次数t2=Timer("test2()","from __main__ import test2")print("append %f second" % t2.timeit(number=1000))t3=Timer("test3()","from __main__ import test3")print("comprehension %f second" % t3.timeit(number=1000))t4=Timer("test4()","from __main__ import test4")print("list range %f second" % t4.timeit(number=1000))-------concat 1.979591 secondappend 0.811599 secondcomprehension 0.375291 secondlist range 0.024658 second```

dict 字典
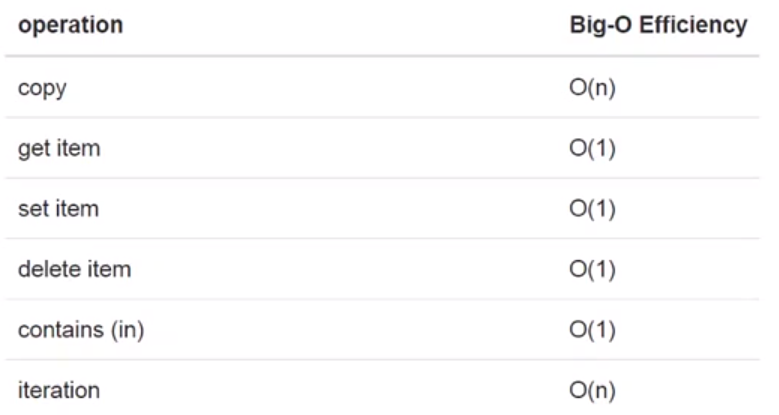
【数据结构与算法Python版学习笔记】算法分析的更多相关文章
- 【数据结构与算法Python版学习笔记】引言
学习来源 北京大学-数据结构与算法Python版 目标 了解计算机科学.程序设计和问题解决的基本概念 计算机科学是对问题本身.问题的解决.以及问题求解过程中得出的解决方案的研究.面对一 个特定问题,计 ...
- 【数据结构与算法Python版学习笔记】查找与排序——散列、散列函数、区块链
散列 Hasing 前言 如果数据项之间是按照大小排好序的话,就可以利用二分查找来降低算法复杂度. 现在我们进一步来构造一个新的数据结构, 能使得查找算法的复杂度降到O(1), 这种概念称为" ...
- 【数据结构与算法Python版学习笔记】基本数据结构——列表 List,链表实现
无序表链表 定义 一种数据项按照相对位置存放的数据集 抽象数据类型无序列表 UnorderedList 方法 list() 创建一个新的空列表.它不需要参数,而返回一个空列表. add(item) 将 ...
- 【数据结构与算法Python版学习笔记】目录索引
引言 算法分析 基本数据结构 概览 栈 stack 队列 Queue 双端队列 Deque 列表 List,链表实现 递归(Recursion) 定义及应用:分形树.谢尔宾斯基三角.汉诺塔.迷宫 优化 ...
- 【数据结构与算法Python版学习笔记】递归(Recursion)——定义及应用:分形树、谢尔宾斯基三角、汉诺塔、迷宫
定义 递归是一种解决问题的方法,它把一个问题分解为越来越小的子问题,直到问题的规模小到可以被很简单直接解决. 通常为了达到分解问题的效果,递归过程中要引入一个调用自身的函数. 举例 数列求和 def ...
- 【数据结构与算法Python版学习笔记】图——最短路径问题、最小生成树
最短路径问题 概念 可以通过"traceroute"命令来跟踪信息传送的路径: traceroute www.lib.pku.edu.cn 可以将互联网路由器体系表示为一个带权边的 ...
- 【数据结构与算法Python版学习笔记】图——骑士周游问题 深度优先搜索
骑士周游问题 概念 在一个国际象棋棋盘上, 一个棋子"马"(骑士) , 按照"马走日"的规则, 从一个格子出发, 要走遍所有棋盘格恰好一次.把一个这样的走棋序列 ...
- 【数据结构与算法Python版学习笔记】图——词梯问题 广度优先搜索 BFS
词梯Word Ladder问题 要求是相邻两个单词之间差异只能是1个字母,如FOOL变SAGE: FOOL >> POOL >> POLL >> POLE > ...
- 【数据结构与算法Python版学习笔记】树——利用二叉堆实现优先级队列
概念 队列有一个重要的变体,叫作优先级队列. 和队列一样,优先级队列从头部移除元素,不过元素的逻辑顺序是由优先级决定的. 优先级最高的元素在最前,优先级最低的元素在最后. 实现优先级队列的经典方法是使 ...
随机推荐
- PyQT5基础布局管理
绝对定位布局 使用move(x, y)可以对窗口进行布局,以窗口左上角为原点,向右为 x 轴正方向,向下为 y 轴正方向,移动(x,y); import sys from PyQt5.QtGui im ...
- 从一个跨二十年的glibc bug说起
1. 缘起 这几天调gcc 7.5.0 +glibc 2.23的交叉编译工具链,由于gcc 7.5.0的默认打开Werr,偶然发现了glibc一个隐藏了二十年的世纪大bug. 这个bug在glibc ...
- Python中 sys.argv[]
sys.argv[]是一个从程序外部获取参数的桥梁,从外部取得的参数可以是多个,所以获得的是一个列表(list),用[]提取其中的元素.其第一个元素是程序本身,随后才依次是外部给予的参数. 实例 im ...
- Python - 执行顺序、执行入口
Python 是如何执行的?执行顺序是怎么样? 至上而下,逐行执行 #!usr/bin/env python # -*- coding:utf-8 _*- """ # a ...
- IPv4掩码与掩码位数的转换
1. 根据掩码获取掩码的位数 int mask2len(unsigned int mask) { /*eg: 255.255.255.0 255.0.255.255.0*/ int bit=0,len ...
- JS008. 跳转缓存滚动条高度并返回时过渡动画(window.pageYOffset & window.scrollTo & SessionStorage)
业务场景 从列表跳转详情页,通过操作返回列表页时,滚动条仍然处于跳转前的高度,并加上 ease-out 的过渡动画. 由于sessionStorage是随页面即关即消的,所以比起VUEX.localS ...
- weblogic漏洞分析之CVE-2017-3248 & CVE-2018-2628
CVE-2017-3248 & CVE-2018-2628 后面的漏洞就是2017-3248的绕过而已,所以poc都一样,只是使用的payload不同 本机开启JRMP服务端 ->利用T ...
- webpack learn2-vue的jsx写法和postcss 1
首先输入命令安装 npm i postcss-loader autoprefixer babel-loader babel-core 在根目录创建文件 .babelrc和postcss.config. ...
- jquery 设置django全局token
通过JQUEYR中的ajaxSetup,来设置django中的token,即不需要再每次都去引用: 第一步: 先django中的html中设置 {% csrf_token %} 第二步: 新一个js ...
- windows2012安装django
第一步:下载python3.6.8或者到(https://www.python.org/downloads/release/python-368/)官网下载(Windows x86-64 execut ...
