OO随笔之魔鬼的第一单元——多项式求导

OO是个借助Java交我们面向对象的课，可是萌新们总是喜欢带着面向过程的脑子去写求导，然后就是各种一面(main)到底、各种方法杂糅，然后就是被hack的很惨。

第一次作业：萌新入门面向对象

题目分析

题目其实不难，最难不过是这种东西的求导：

+4*x - -x^2 + x　　

其实很好办啊，直接超级长的一个正则表达式莽，如图。

String pattern = "..."；//好长的一段
String longPattern = "pattern(pattern)+";

于是这次作业那些一百多个字符长的正则表达式就来了，思想就是整体匹配，然后就被hack地爆栈了（GG。当然，正则可不是给你这样操作的，正则更加适合于那些特征性强的长度也不是很长的串的识别。一个更好的办法是逐项匹配，匹配到一项就存起来再匹配下一项，然后求导化简一气呵成。

整体思路是对读入进行一些处理，比如排除掉一些错误字符、判断空格位置和合法性、格式化字符串以便逐项匹配，然后利用简单的正则表达式匹配第一项并实例化一个Poly类，利用通项a*x^b进行储存（这里可以利用HashMap或者暴力for循环合并下同类项）。然后就可以求导了。输出的时候也要分类：将系数为0，系数为1和系数为-1的情况；指数为0，指数为1的情况分类输出。

题目不难，思路也清楚，问题在于不知道面向对象是个什么东西。就比如我的架构：

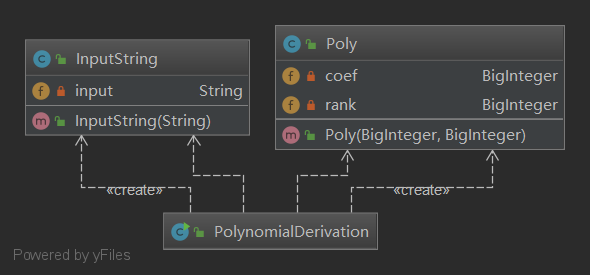
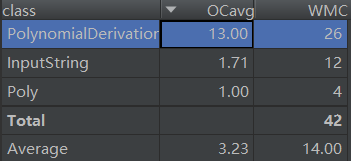
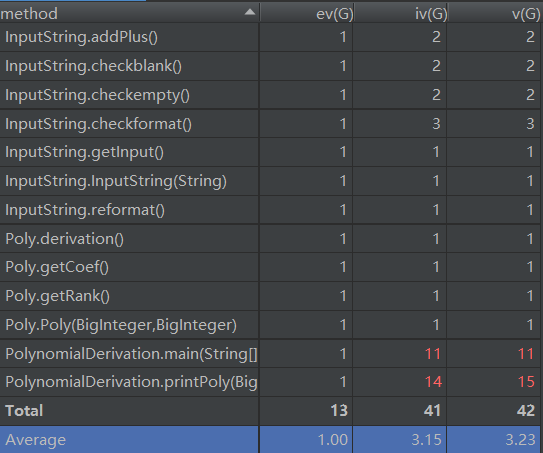
我把逐项匹配、输出优化全部放在了主类PolynomialDerivation里面，然后复杂度就爆炸了，单个方法也是逼近60行边界。虽然说类比较少，但是我main里面什么都有，各种功能胡乱炖，这代码风格就很差了，读起来颇有C的感觉。

发现问题

主要是大家的写法都很C-style，功能混杂，面向过程。

次要是正则表达式不够完善，比如少了一个[\t ]，没有处理非法字符，当然也有一些刀友采取了不是很好的处理输入的方案，导致一些诡异的数据点会报错，比如 +或者500个+x。

再次要问题是刀不够长，我一开始采取简单的蒙眼扔弹法，手动造数据，然后蒙着眼睛给房间七兄弟扔一发，结果就是伤害真的不行。后来通过看正则表达式也有所收获，但总体还是消耗体力来刀人。

第二次作业：萌新尝试面向对象

题目分析

第二次作业学乖了，考虑到有幂函数和三角函数两种情况，同学们开始用继承啊接口啊操作，或者，用一种“面向题目”的办法：找到一个通项a*x^b*sin(x)^c*cos(x)^d，然后甚至可以不用对sin、cos的类进行求导，而是直接对这个通项类（Item类）进行求导，得到三项，分别都为Item类，然后通过HashMap或者for循环合并同类项完事（dalao：加一层三角恒等变换也行）。这个看似巧妙的办法很好的简化了类的功能需求，”面向题目“地解决了问题，将可拓展性抛掷脑后。我相信很多人也是这样写的；而这显然有违代码风格中的“开闭原则”——可以基于你的代码进行拓展，但不能修改你的代码，毕竟通项这种东西可遇而不可求。

这一节标题是尝试面向对象，那么相比第一次的main.c，这次又有什么不同呢。

• 将功能分离，对于+3*x^2*sin(x)-cos(x)，将其分为+3*x^2*sin(x)这样的一个实例，再分为3和x^2和sin(x)这三个基类的实例，拥有了基本的界限和分工

• 对于类内部保持了封闭和不可见，至少在语法层面有了封装

• 接口和抽象类的使用开始出现

• dalao们的其他骚操作，比如Factory和assert

我的设计也更加的有层次感，虽然依旧存在着主类中功能较多，类较少，功能混杂，“面向题目”过于明显而扩展性较差的问题，隐约感觉到我第三次作业要爆肝重构了。

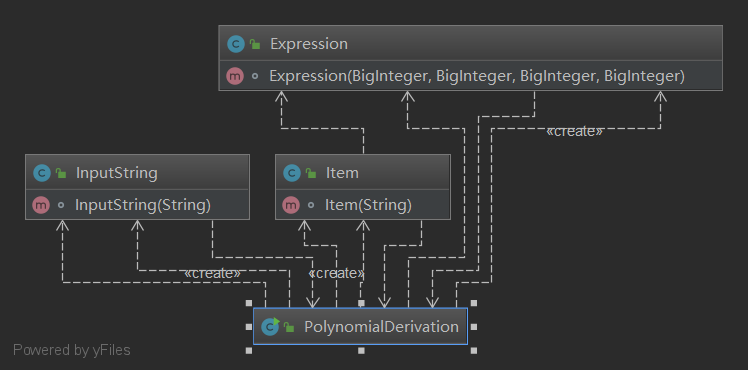
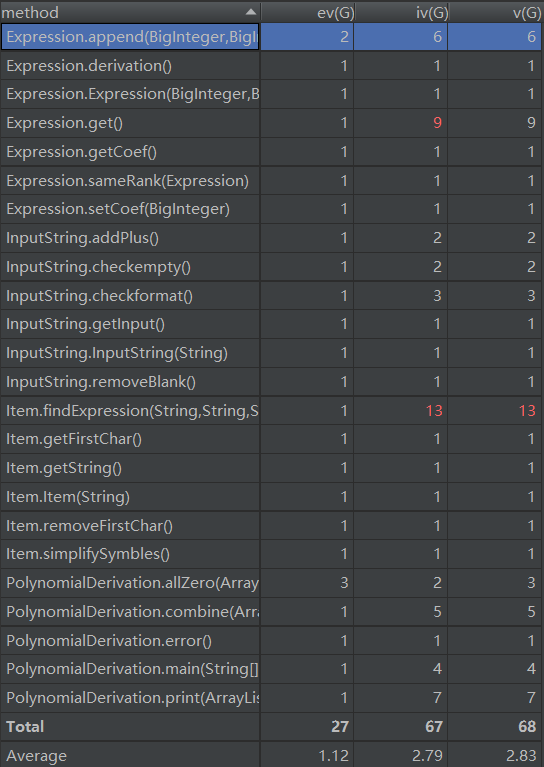
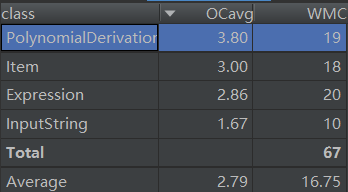
这次作业中复杂性比较高的方法是在一长串输入的字符串找到一个个的项（即通项），因为这个方法不仅仅涉及了循环处理字符串寻找通项，也兼职了用matcher.group()方法取得其中的有效信息的任务，导致这个方法比较复杂；但是它可以被拆解成两个方法：一个负责matcher.find()，另一个负责用group()取得数据，他们之间通过传递Matcher类的参数来沟通。

发现问题

这次的强测错了几个点，然后分到了腥风血雨的C组，各种你捅我一刀我还你两刀，最后被砍七刀。后来公布数据之后我才发现，当初一个小小的疏忽，贪图简单把1*x这种系数为1的情况的化简写成了replace("1*","")。单纯的将1*给替换掉，乍一看好像是没有错的，但是我却忽略了当系数为11、21、31...的时候，乃至所有系数个位为1的项，甚至x^1*sin(x)这样的项，几乎都是错的。

第三次作业：萌新胡乱面向对象

题目分析

写完第二次作业以后，我就开始了对代码的重构，因为自己对于面向对象有有了新的理解，以前代码许多不规范不区分的东西，都需要重新分门别类，于是我将输入模块拿出，将一些过长的方法重新理清。

首先是不能依靠正则表达式了，Java的正则仿佛不能处理嵌套的问题，而且由于第一次作业就有深层递归导致爆栈的问题出现，这种一层又一层的就不能直接一个正则往上写了，而需要剥洋葱。

其次是类的职责需要分的更加清楚，我现在有一种想法就是把题目中所有出现过的对象都作为一个类，不论大小不论耦合，然后再去分析其中的关系。就比如逛菜市场，先无脑把所有的每一种的食材都建立一个类，然后再考虑这个属于鱼、那个属于青菜这样的分类，建立父类或者接口。这样的分类法，应该能更好的将对象分离。

考虑第三次的任务，我和很多同学一样，建立了一棵树，树中的元素为两种类：Expression类（负责解析形如1+1的式子），Item类（负责解析形如1*1的式子），并且他们继承自一个公共的父类Factor（负责处理sin(x)这样的简单表达式）。

我的大概想法是这样：一个表达式解析成Expression类，然后按照+号或者-号分割成若干个Item类，Item类中再依据*号切割成若干个Expression类……直到最后剩下一个形如1、x、sin(x)这样的简单因子，但是在处理过程中，慢慢的发现自己设计的不合理之处：第一Expression类同时也肩负着处理形如sin(((x+4)*cos(x)))这样的表达式中的sin部分的责任，第二Expression类结点的子结点只能为Item类，Item类的子结点只能为Expression类。这两个问题在我实际在写的时候才发现，处理起来逻辑上比较麻烦，甚至需要东拼西凑。也正因此，在写完之后的测试过程中，我经历了长期的修补过程；最后的程序也不是完美的。

最后写出来的类比较少（相比其他同学），只有六个；我分析了下，这是因为自己类的作用混合性很高，比如Factor类可以识别并处理简单因子，同时又包含了三种简单因子的求导方法，更还有Expression类和Item类共用的切割字符串中因子的方法；如果重构的话，我会将其分为两个类：真正的Factor类（负责处理1、x、sin(x)这样的简单因子）和一个Expression、Item类的公共父类，同时Factor类又可以包含三个子类，分别用来处理纯数字、x的幂、三角函数的幂。“胡乱面向对象”指的就是我这样各种元素混在一起写成一个类然后出现各种各样的bug的操作。

发现问题

在互测中，我自己发现的bug就是因为自己胡乱一波操作导致的：Expression类由于兼职了处理形如sin(((x+4)*cos(x)))这样的表达式中的sin部分的责任，而在按照括号切割的时候，面对sin(x)*(x)这种伪sin(x)型的式子，就出现了bug；在面对sin(cos(((x))))这种多个括号嵌套三角函数的时候，也出现了bug。所以这些bug如果好好写对象，不要一股脑用面向过程的思想去莽，也不会出现。

除了bug之外，就是方法和类的复杂性和耦合性比较高，如图。

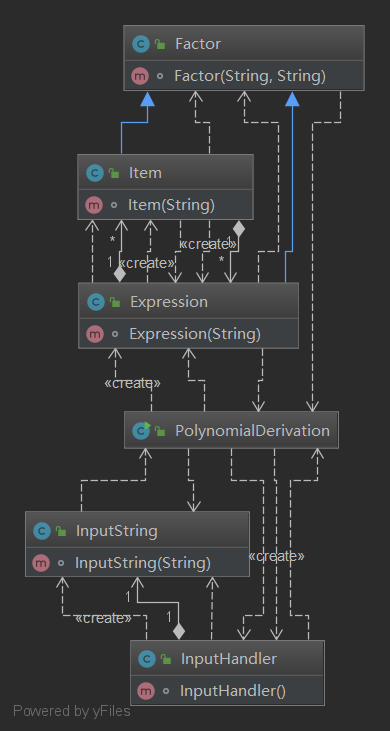
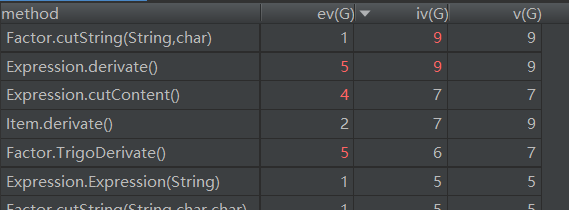
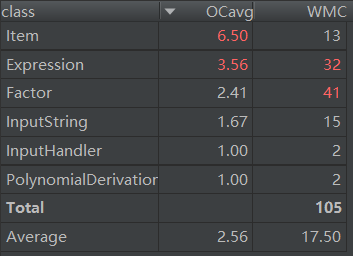
从图中可以看出，几乎每个类都和其他类有直接的关系，所以关系错综复杂；这也是我设计的缺漏导致的代码风格的不佳。

方法复杂度我只展示了复杂度最高的的几个方法，其中主要是切割字符串cutString方法、求导的derivate方法比较复杂。因为cutString方法我是用for循环来遍历字符串并且用ArrayList来接收结果，而derivate方法涉及到了多重的递归调用和复杂的乘法求导的法则，故这两个方法比较复杂。

另外，由于使用的类相对比较少，类之间的平行性也不是很强，我也懒得去写接口了，似乎没有这个的必要。

互测中发现的bug，并没有特别强的典型性，应该都是因为架构的小瑕疵导致的，不过根据观察，计算错误的比较少，反而是因为某些特殊数据导致的爆栈或异常然后输出了WRONG FORMAT!。

在三次的刀人的过程中，我找bug的能力也越来越强，虽然依旧停留在用炸弹炸鱼的老思想，但是用的装备越来越成熟了。第一次作业的时候是典型的蒙眼手动炸人，第二次开始写了一些基于命令行的脚本，能够自动根据输入将所有人的输出都列出来，第三次借用了别人的数据生成器然后自动带入数据比对出大家的对与错。虽然不知道以后还用不用得着这种工具，但是自己也懂得了很多课外的、其他语言的用法，增长了见识。同时结合自动数据和手动的点对点数据的轰炸，在刀人方面也成了一个“狼人”。