[省选联考 2021 A 卷] 矩阵游戏

很巧妙的一个构造。

我是没有想到的。

自己的思维能力可能还是不足。

考虑先满足\(b\)对\(a\)的限制，把\(a\)的第一行和第一列设\(0\)，推出这个\(a\)。

接下来考虑对这个\(a\),矩阵进行一些行列加的操作满足\(\leq 1e6\)的性质。

考虑操作做时，奇偶分开加减这样的操作保证\(b\)的限制。

借用一下其他大佬的图。

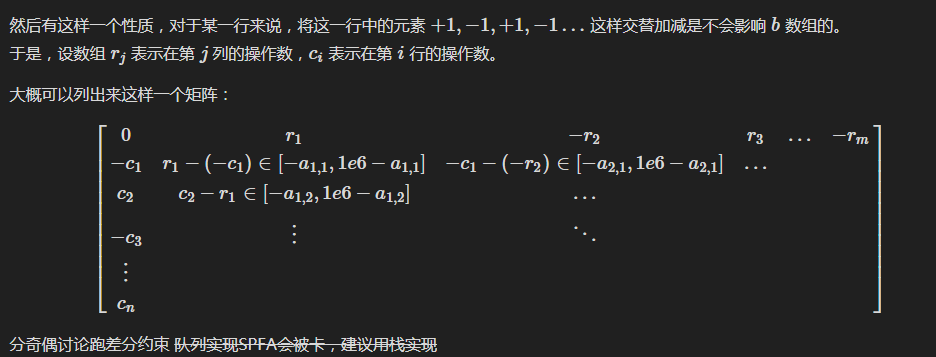
如下代码因为被卡常了，所以在跑\(BellmanFord\)时没有跑完，所以其实并不保证正确性。只是能过数据而已，好无奈。

[省选联考 2021 A 卷] 矩阵游戏

#include<iostream>
#include<cstdio>
#include<cstring>
#define ll long long 
ll N;
int n,m;
int a[4000][4000],b[4000][4000],cnt,head[100000];
ll dis[100000];
struct P{int s,to,next,v;}e[400000];
inline void clear(){cnt = 0;std::memset(head,0,sizeof(head));std::memset(dis,0x3f,sizeof(dis));}
inline void add(ll x,ll y,ll v){
//	std::cout<<x<<" "<<y<<" "<<v<<std::endl;
	e[++cnt].s = x;
	e[cnt].to = y;
	e[cnt].next = head[x];
	e[cnt].v = v;
	head[x] = cnt;
}
inline int read(){
	int ans = 0;
	char a = getchar();
	while(a < '0' || a > '9')a = getchar();
	while(a <= '9' && a >= '0')
	ans = (ans << 3) + (ans << 1) + (a - '0'),a = getchar();
	return ans;
}
inline void init(){
	n = read(),m = read();
	for(int i = 1;i <= n - 1;++i)
	for(int j = 1;j <= m - 1;++j)
	b[i][j] = read();
}
inline void st(){
	for(int i = n;i >= 1;--i)
	for(int j = m;j >= 1;--j)
	a[i][j] = b[i][j] - a[i + 1][j] - a[i + 1][j + 1] - a[i][j + 1];
}
inline bool r(){
	dis[1] = 0;
	for(int i = 1;i <= n;++i){
		for(int j = 1;j <= cnt;++j){
			int s = e[j].s;
			int t = e[j].to;
			if(dis[t] > dis[s] + e[j].v)
			dis[t] = dis[s] + e[j].v;
//			std::cout<<s<<" "<<t<<" "<<dis[t]<<" "<<dis[s]<<" "<<e[j].v<<std::endl;
		}
	}
//	for(int i = 1;i <= m + n;++i)
//	std::cout<<dis[i]<<" ";
	for(int j = 1;j <= cnt;++j){
			int s = e[j].s;
			int t = e[j].to;
			if(dis[t] > dis[s] + e[j].v){
				return false;
			}
	}
	return true;
}
inline void putout(){
//	for(int i = 1;i <= m + n;++i)
//	std::cout<<dis[i]<<" ";
	puts("YES");
//	for(int i = 1;i <= n;++i,puts(""))
//	for(int j = 1;j <= m;++j)
//	std::cout<<a[i][j]<<" ";
	for(int i = 1;i <= n;++i,puts(""))
	for(int j = 1;j <= m;++j){
		if(!((i + j) & 1))
		a[i][j] = a[i][j] + dis[i] - dis[n + j];
		else
		a[i][j] = a[i][j] + dis[j + n] - dis[i];
		std::cout<<a[i][j]<<" ";
	}
}
inline void got(){
	clear();
	for(int i = 1;i <= n;++i){
		for(int j = 1;j <= m;++j){
		if(!((i + j) & 1))
		add(i,j + n,a[i][j]),add(j + n,i,1000000 - a[i][j]);
		else
		add(j + n,i,a[i][j]),add(i,j + n,1000000 - a[i][j]);
		}
	}
//	for(int i = 1;i <= m + n;++i)
//	add(0,i,0);
	if(!r())
	puts("NO");
	else
	putout();
}
int main(){
	scanf("%d",&N);
	while(N -- ){
		init();
		st();
		got();
	}
}