xf浅谈_最短路

最短路问题（short-path problem）：最短路问题是图论研究中的一个经典算法问题，指在寻找图（由结点和路径组成的）中两结点之间的最短路径。算法具体的形式包括：

1.确定起点的最短路径问题 - 即已知起始结点，求最短路径的问题。

2.确定终点的最短路径问题 - 与确定起点的问题相反，该问题是已知终结结点，求最短路径的问题。在无向图中该问题与确定起点的问题完全等同，在有向图中该问题 等同于把所有路径方向反转的确定起点的问题。

3.确定起点终点的最短路径问题 - 即已知起点和终点，求两结点之间的最短路径。

4.全局最短路径问题 - 求图中所有的最短路径。

---

以一个故事开头吧：

这又是晴朗的一天，XF准备去旅行，但他这次想去看自由男神像。所以他正在用千度查一查机票的价格：

出发地			目的地      		单价
夫代尔马			自由男神像		15000 yuan
浮卢宫			尼悉歌剧院		100 yuan
尼悉歌剧院		自由男神像		1000 yuan
夫代尔马			浮卢宫			10 yuan

XF现在住在夫代尔马，他发现直接由夫代尔马去自由男神像会比夫代尔马->浮卢宫->尼悉歌剧院->自由男神像花费的钱多一些，~~或者说，多得多。。。~~所以他决定选择
夫代尔马->浮卢宫->尼悉歌剧院->自由男神像这一条便宜的方案！！！

---

故事结束！

那么，我们把XF的机票选择方案扩大很多很多倍，且让XF住的地方变来变去，就成为了求一个多源最短路径的题啦！！
那么对于这类问题，我们应该砸么做类？？

Floyd算法隆重出场！！！

首先，我要问一个问题：为什么两个顶点的最短距离为什么不是它们的直接距离呢？？？
局外读者:“因为他们有可能没有直接连接的边，而是由一个或多个中继顶点间接连接的啊！！！”
对啦！真聪明！！！
举个栗子：

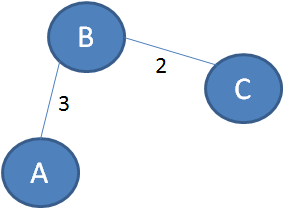
上图的顶点A和顶点C没有直接相连的边，它们之间没有直接距离。
如果以B作为“中继顶点”，此时A到C的最短路径就是A-B-C，最短距离是3+2=5
那么，再举个栗子：
上图的顶点A和顶点C直接相连，距离是6。但是存在一条“迂回”路径A-B-C，距离是3+2=5<6。
所以，经过中继顶点B，从A到C的最短距离是5。
这就是弗洛伊德算法的核心思想，我们利用这些中继顶点，一步一步推导出图中所有顶点的最短距离；
下面我们来看一看Floyd算法的详细步骤。

1. 要实现Floyd算法，首先需要构建带权图的邻接矩阵：
   
   在邻接矩阵当中，每一个数字代表着从某个顶点到另一个顶点的直接距离，这个距离是没有涉及到任何中继顶点的。
2. 此时假定只允许以顶点A作为中继顶点，那么各顶点之间的距离会变成什么样子呢？
   B和C之间的距离原本是无穷大，此时以A为中继，距离缩短为AB距离+AC距离=
   5+2=7。
   更新对应矩阵元素（橙色区域代表顶点A到其他顶点的临时距离：
   
3. 接下来以顶点A、B作为中继顶点，那么各顶点之间的距离会变成什么样子呢？
   A和D之间的距离原本是无穷大，此时以B为中继，距离缩短为AB距离+BD距离=5+1=6。
   A和E之间的距离原本是无穷大，此时以B为中继，距离缩短为AB距离+BE距离=5+6=11。
   更新对应矩阵元素（橙色区域代表顶点B到其他顶点的临时距离）：
   
4. 接下来以顶点A、B、C作为中继顶点，那么各顶点之间的距离会变成什么样子呢？
   A和F之间的距离原本是无穷大，此时以C为中继，距离缩短为AC距离+CF距离=2+8=10。
   更新对应矩阵元素（橙色区域代表顶点C到其他顶点的临时距离）：
   以此类推，我们不断引入新的中继顶点，不断刷新矩阵中的临时距离。
   最终，当所有顶点都可以作为中继顶点时，我们的距离矩阵更新如下：

此时，矩阵中每一个元素，都对应着某顶点到另一个顶点的最短距离。
让我们回顾一下动态规划的两大要素：

问题的初始状态
问题的状态转移方程式

对于寻找图的所有顶点之间距离的问题，初始状态就是顶点之间的直接距离，也就是邻接矩阵。
而问题的状态转移方程式又是什么呢？
假设新引入的中继顶点是n，那么：
顶点i 到 顶点j 的新距离 = Min（顶点i 到 顶点j 的旧距离，顶点i 到 顶点n 的距离+顶点n 到 顶点j 的距离
所以：

弗洛伊德是一种基于动态规划的多源点最短路算法！

---

回到故事，如果XF就一直住在夫代尔马呢？？
那么，这就转换为一道单源最短路径问题了。。。

Dijkstra算法隆重出场！！！

究竟什么是迪杰斯特拉算法？它是如何寻找图中顶点的最短路径呢？
这个算法的本质，是不断刷新起点与其他各个顶点之间的 “距离表”。
让我们来演示一下迪杰斯特拉的详细过程：

1. ，创建距离表。表中的Key是顶点名称，Value是从起点A到对应顶点的已知最短距离。但是，一开始我们并不知道A到其他顶点的最短距离是多少，Value默认是无限大

2. ，遍历起点A，找到起点A的邻接顶点B和C。从A到B的距离是5，从A到C的距离是2。把这一信息刷新到距离表当中：

3. ，从距离表中找到从A出发距离最短的点，也就是顶点C。

4. ，遍历顶点C，找到顶点C的邻接顶点D和F（A已经遍历过，不需要考虑）。从C到D的距离是6，所以A到D的距离是2+6=8；从C到F的距离是8，所以从A到F的距离是2+8=10。把这一信息刷新到表中：
   接下来重复第3步、第4步所做的操作：

5. ，也就是第3步的重复，从距离表中找到从A出发距离最短的点（C已经遍历过，不需要考虑），也就是顶点B。

6. ，也就是第4步的重复，遍历顶点B，找到顶点B的邻接顶点D和E（A已经遍历过，不需要考虑）。从B到D的距离是1，所以A到D的距离是5+1=6，小于距离表中的8；从B到E的距离是6，所以从A到E的距离是5+6=11。把这一信息刷新到表中：（在第6步，A到D的距离从8刷新到6，可以看出距离表所发挥的作用。距离表通过迭代刷新，用新路径长度取代旧路径长度，最终可以得到从起点到其他顶点的最短距离）

7. ，从距离表中找到从A出发距离最短的点（B和C不用考虑），也就是顶点D。

8. ，遍历顶点D，找到顶点D的邻接顶点E和F。从D到E的距离是1，所以A到E的距离是6+1=7，小于距离表中的11；从D到F的距离是2，所以从A到F的距离是6+2=8，小于距离表中的10。把这一信息刷新到表中：
   （过了一百年——————）
   
   就这样，除终点以外的全部顶点都已经遍历完毕，距离表中存储的是从起点A到所有顶点的最短距离。显然，从A到G的最短距离是11。（路径：A-B-D-F-G）

弗洛伊德代码实现：

#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
using namespace std;

int n,m,x,y;
long long dp[505][505];
int pre[505][505];

void HH(int z){
	if(pre[x][z]==0)
		return ;
	HH(pre[x][z]);
	printf("%d ",z);
}

int main(){
	cin>>n>>m;
	for(int i=1;i<=n;i++){
		for(int j=1;j<=n;j++)
			dp[i][j]=214748360;
	}
	for(int i=1;i<=m;i++){
		int sum;
		cin>>x>>y>>sum;
		dp[x][y]=sum;
		pre[x][y]=x;
	}
	for(int k=1;k<=n;k++){
		for(int i=1;i<=n;i++){
			for(int j=1;j<=n;j++){
				if(dp[i][j]>dp[i][k]+dp[k][j]){
					dp[i][j]=dp[i][k]+dp[k][j];
					pre[i][j]=pre[k][j];
				}
			}
		}
	}
	cin>>x>>y;
	cout<<dp[x][y]<<endl;
	printf("%d ",x);
	HH(y);
	return 0;
}

Dijkstra算法:

#include<bits/stdc++.h>
using namespace std;
int n,m,x,y;
bool flag[5005]={};
int dp[5005][5005],f[5005];
int main(){
	cin>>n>>m>>x>>y;
	memset(dp,0x3f,sizeof(dp));
	memset(f,0x3f,sizeof(f));
	for(int i=1;i<=m;i++){
		int xx,yy,zz;
		scanf("%d %d %d",&xx,&yy,&zz);
		dp[xx][yy]=dp[yy][xx]=zz;
	}
	f[x]=0;
	flag[x]=0;
	for(int i=1;i<=n;i++){
		int Minn=0x3f3f3f3f;
		int k=0;
		for(int j=1;j<=n;j++){
			if(flag[j]==0&&(f[j]<Minn)){
				Minn=f[j];
				k=j;
			}
		}
		if(k==0) continue;
		flag[k]=1;
		for(int j=1;j<=n;j++){
			if(f[j]>f[k]+dp[k][j]){
				f[j]=f[k]+dp[k][j];
			}
		}
	}
	printf("%d",f[y]);
	return 0;
}