6.6考试总结(NOIP模拟4)

前言

考试这种东西暴力拉满就对了QAQ

T1 随

题解

解题思路

DP+矩阵乘（快速幂）+数论

又是一道与期望无关的期望题，显然答案是 总情况/情况数（\(n^m\)）。

接下来的问题就是对于总情况的求和了。题目下面就给出了一个很好的概念：原根。

求原根

再看一下mod的值，不会错了，暴力求就行。根据原根的性质，判断枚举元素的 \(1\sim p-2\) 次方有没有在\(\mod p\)意义下等于 1 。

int get_Yuan()
{
	for(int i=2;i<=p;i++)
	{
		int temp=1;
		bool vis=true;
		for(int j=1;j<p-1;j++)
		{
			temp=temp*i%p;
			if(temp==1)
			{
				vis=false;
				break;
			}
		}
		if(vis)
			return i;
	}
}

原根用途

有了原根，我们就可以把几个数的乘积换成指数级别的加法了。

最后的结果也就是\(k_0\times g^0+k_1\times g^1+...+k_{p-1}\times g^{p-1}\)

k就是每一个答案（g的若干次幂）出现的次数，计算$ k_i$ 就是从n个元素中取m次，取出的数的次方之和等于i，可以矩阵乘加速

优化

如果模数是一质数，在计算快速幂的时候，可以直接把指数%(p-1)。

我们的矩阵计算的就是指数之和，所以关于矩阵的所有模数都是p-1,这样以来矩阵的规模也就缩小到了\((p-1)\times(p-1)\)，并且可以采用矩阵快速幂。

注意

整个过程中mod的值有所变化：

• 计算原根以及原根的若干次幂的时候，模数是p
• 计算矩阵的时候，因为计算的是原根的指数和，模数是p-1
• 计算答案的时候，模数是1e9+7

再求幂以及log时，算到p-2就刚刚好，至于比他大的部分，在之后的运算中如果加上就会导致结果偏大，所以直接不初始化，值为0就好了。

code

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e5+10,mod=1e9+7;
int n,m,p,yg,sum,base,mi[N],lg[N],s[N];
int get_Yuan()
{
	for(int i=2;i<=p;i++)
	{
		int temp=1;
		bool vis=true;
		for(int j=1;j<p-1;j++)
		{
			temp=temp*i%p;
			if(temp==1)
			{
				vis=false;
				break;
			}
		}
		if(vis)
			return i;
	}
}
int ksm(int x,int y)
{
	int ans=1;
	while(y)
	{
		if(y&1)
			ans=ans*x%mod;
		y>>=1;
		x=x*x%mod;
	}
	return ans;
}
struct jz
{
	int h[1005];
	void clear()
	{
		memset(h,0,sizeof(h));
	}
	jz operator *(const jz &a) const
	{
		jz ans;
		ans.clear();
		for(int i=0;i<p-1;i++)
			for(int j=0;j<p-1;j++)
				ans.h[(i+j)%(p-1)]=(ans.h[(i+j)%(p-1)]+h[i]*a.h[j])%mod;
		return ans;
	}
}a,answer;
jz ksm(jz x,int y)
{
	jz ans;
	ans.clear();
	ans.h[lg[1]]=1;
	while(y)
	{
		if(y&1)
			ans=ans*x;
		y>>=1;
		x=x*x;
	}
	return ans;
}
#undef int
int main()
{
	#define int register long long
	#define ll long long
	scanf("%lld%lld%lld",&n,&m,&p);
	yg=get_Yuan();
//	cout<<yg<<endl;
	base=ksm(ksm(n,m),mod-2);
	if(p==2)
	{
		cout<<1;
		return 0;
	}
	mi[0]=1;
	for(int i=1;i<p-1;i++)
	{
		mi[i]=mi[i-1]%p*yg%p;
		lg[mi[i]]=i;
//		cout<<mi[i]<<endl;
	}
	for(int i=1;i<=n;i++)
		scanf("%lld",&s[i]);
	for(int i=1;i<=n;i++)
		a.h[lg[s[i]]]++;
	answer=ksm(a,m);
	for(int i=0;i<p-1;i++)
		sum=(sum+mi[i]*answer.h[i]%mod)%mod;
	printf("%lld",sum*base%mod);
	return 0;
}

T2 单

题解

解题思路

看遍网上题解都说是个高级的 换根DP 感觉有一点关系，但不知道也无妨。

先看暴力

暴力思路比较好像，对于t=1的情况直接Dij或者LCA，DFS也行；t=2的式子一看就可以高斯消元，要注意的就是卡一下精度，开double，输出的时候手动四舍五入或者加上一个1e-12也可以输出整数位，但是绝不能int强制转化！！！

\(code\)

再看正解

令\(sum[i]\)表示以 i 为根的子树的 a 之和。

t=0

可以得出式子：\(b[now]=(b[fa]-sum[now])+(sum[1]-sum[now])\)

以下图为例

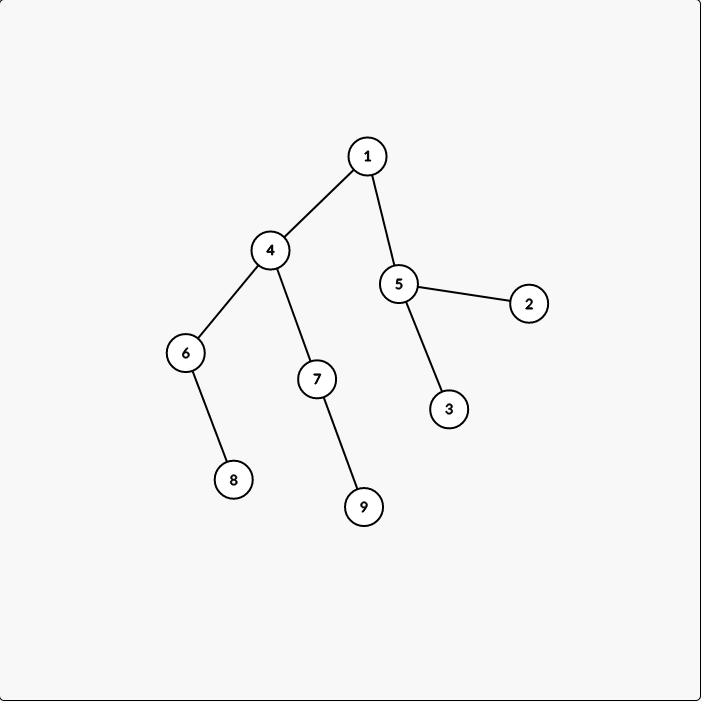
假设\(now=6\)，那么 \(fa=4\)，将数值由fa转移到now

此时我们把整棵树划分为两部分：

• A：以 6 为根节点的子树
• B：其他部分

现在，式子的前半部分就是fa的b减去now子树部分的a，这就是now子树对于b[now]的贡献以及B部分的部分贡献，相比于fa，now相较于B的深度多一，因此要加上\(sum[1]-sum[now]\)。这一块的式子很妙，可以多思考一下。

然后进行 DFS 求出 sum 数组，进而求出 b 数组就好了。

t=1

和t=1的式子有一定的关系，移一下项：

\(b[now]-b[fa]=sum[1]-sum[now]\)

求一下和：

\(\sum\limits_{i=2}^nb[i]+b[fa(i)]=sum[1]\times(n-1)-2\times\sum\limits_{i=2}^nsum[i]\)

也就是：

\(x_1b[1]+x_2b[2]+...+x_nb[n]=(n-1)sum[1]-2\times\sum\limits_{i=2}^nsum[now]\)

与前面的换根的思路相似，不难发现\(2\times\sum\limits_{i=2}^nsum[now]\)其实就是\(b[1]\),在此不做过多赘述。

然后进行DFS求出每个系数x，然后就可以求出sum[1]

再进行DFS求一下其他的sum。

\(now=1\)时需要特殊处理，如果由以上式子求的话显然会出现负数，直接求LCA或者堆优化Dij，DFS都可以求。

然后再再进行DFS求出整棵树的a就好了。

code

#include<bits/stdc++.h>
#define int long long
//#define double long double
using namespace std;
const int N=1e5+10,M=1e4+10;
int T,n;
int dis[N],sum[N],s[N];
int tot,T_temp,head[N],nxt[N<<1],ver[N<<1],a[N],b[N];
inline void add_edge(int x,int y)
{
	ver[++tot]=y;
	nxt[tot]=head[x];
	head[x]=tot;
}
void dfs(int x,int fa,int dep)
{
	b[1]+=a[x]*dep;
	for(int i=head[x];i;i=nxt[i])
	{
		int to=ver[i];
		if(to==fa)
			continue;
		dfs(to,x,dep+1);
	}
}
void dfs1(int x,int fa)
{
	for(int i=head[x];i;i=nxt[i])
	{
		int to=ver[i];
		if(to==fa)
			continue;
		dfs1(to,x);
		sum[x]+=sum[to];
	}
	sum[x]+=a[x];
}
void dfs2(int x,int fa)
{
	b[x]=b[fa]+sum[1]-2*sum[x];
	for(int i=head[x];i;i=nxt[i])
	{
		int to=ver[i];
		if(to==fa)
			continue;
		dfs2(to,x);
	}
}
inline void work_B()
{
	dfs(1,0,0);
	dfs1(1,0);
	for(int i=head[1];i;i=nxt[i])
		dfs2(ver[i],1);
	for(int i=1;i<=n;i++)
		printf("%lld ",b[i]);
	printf("\n");
}
void dfs3(int x,int fa)
{
	s[x]++;
	s[fa]--;
	for(int i=head[x];i;i=nxt[i])
	{
		int to=ver[i];
		if(to==fa)
			continue;
		 dfs3(to,x);
	}
}
void dfs4(int x,int fa)
{
	sum[x]=(b[fa]-b[x]+sum[1])/2;
	for(int i=head[x];i;i=nxt[i])
	{
		int to=ver[i];
		if(to==fa)
			continue;
		 dfs4(to,x);
	}
}
void dfs5(int x,int fa)
{
	int temp=sum[x];
	for(int i=head[x];i;i=nxt[i])
	{
		int to=ver[i];
		if(to==fa)
			continue;
		dfs5(to,x);
		temp-=sum[to];
	}
	a[x]=temp;
}
inline void work_A()
{
	memset(s,0,sizeof(s));
	int temp=0;
	for(int i=head[1];i;i=nxt[i])
		dfs3(ver[i],1);
	for(int i=1;i<=n;i++)
		temp+=s[i]*b[i];
	sum[1]=(temp+2*b[1])/(n-1);
	for(int i=head[1];i;i=nxt[i])
		dfs4(ver[i],1);
	dfs5(1,0);
	for(int i=1;i<=n;i++)
		printf("%lld ",a[i]);
	printf("\n");
}
inline void work()
{
	tot=0;
	memset(ver,0,sizeof(ver));
	memset(head,0,sizeof(head));
	memset(nxt,0,sizeof(nxt));
	memset(sum,0,sizeof(sum));
	scanf("%lld",&n);
	for(int i=1,x,y;i<n;i++)
	{
		scanf("%lld%lld",&x,&y);
		add_edge(x,y);
		add_edge(y,x);
	}
	scanf("%lld",&T_temp);
	if(T_temp)
	{
		memset(a,0,sizeof(a));
		for(int i=1;i<=n;i++)
			scanf("%lld",&b[i]);
		work_A();
	}
	else
	{
		memset(b,0,sizeof(b));
		for(int i=1;i<=n;i++)
			scanf("%lld",&a[i]);
		work_B();
	}
}
#undef int
int main()
{
	#define int register long long
	#define ll long long
	scanf("%lld",&T);
	while(T--)
		work();
	return 0;
}

T3 题

题解

解题思路

一看这题名字挺奇怪，网上一搜，是一套题（简，单，题）好像时学长出的，因为简太水了，就被教练踢掉了。

看见这个题的第一思路先是DP，随后想了想排列组合好像更好一些，最后一看时间不够了，先打了一个样例（5pts）然后就是大暴力了。

下面就是正解了：

typ=0

枚举横向移动了多少步。

横向移动i步时(为了存在合法解,i必须是偶数)，纵向的显然就是n-i了，横向方案数为\(C_i^{\frac{i}{2}}\)(来回随便走i步里面选\(\dfrac{i}{2}\)步

纵向就是\(C_{n-i}^{\frac{n-i}{2}}\)，和横向的式子差不多。

然后从n步里选i步，乘上一个\(C_n^i\)就好了。

typ=1

从\(\dfrac{n}{2}\)个-1和\(\dfrac{n}{2}\)个1里排列一下，这不就是个Catalan序列吗 （虽然我是现学的） 。

typ=2

这里就用上DP了

f[i]表示走了i步回到原点的方案数（中途可能回到过原点多次

枚举第一次回到原点时走过的步数j(为了存在合法解,j为偶数)

则此时方案数为\(f[i-j]*Catalan(j/2-1)\)

第 j 步第一次回到原点，之后可能有多次再次回原点\(f[i-j]\)，

在计算这 j 步时，我们必须保证 j 步中不回原点，所以\(Catalan(j/2-1)\)

这个 -1 就是保证栈不为空 (左右移动可以看作栈)

typ=3

与typ=1的做法有一点类似。

枚举横向移动了多少步

横向移动 i 步时(为了存在合法解, i 必须是偶数)

方案数为\(C_n^i*Catalan(\dfrac{i}{2})*Catalan(\dfrac{n-i}{2})\)

代码优化

因为要取模，就一定要计算 inv ，又可以发现我们用的所有inv都是阶乘，因此我们可以直接把inv初始化阶乘。对于其他的快速幂一下就好了。

code

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e5+10,mod=1e9+7;
int n,ans,task,f[N],jc[N<<1],inv[N<<1];
void get_Jc()
{
	jc[0]=1;
	for(int i=1;i<(N<<1);i++)
		jc[i]=jc[i-1]*i%mod;
}
void get_Inv()
{
	inv[0]=inv[1]=1;
	for(int i=2;i<(N<<1);i++)
		inv[i]=(mod-mod/i)*inv[mod%i]%mod;
	for(int i=1;i<(N<<1);i++)
		inv[i]=inv[i]*inv[i-1]%mod;
}
int ksm(int x,int y)
{
	int ans=1;
	while(y)
	{
		if(y&1)
			ans=ans*x%mod;
		y>>=1;
		x=x*x%mod;
	}
	return ans;
}
int C(int i,int j)
{
	if(i>j)
		return 0;
	if(i==0||j==0)
		return 1;
	return jc[j]%mod*inv[i]%mod*inv[j-i]%mod;
}
int Catalan(int x)
{
	return C(x,x<<1)%mod*ksm(x+1,mod-2)%mod;
}
#undef int
int main()
{
	#define int register long long
	#define ll long long
	scanf("%lld%lld",&n,&task);
	get_Jc();
	get_Inv();
	if(task==0)
	{
		for(int i=0;i<=n;i+=2)
			ans=(ans+C(i,n)%mod*C(i>>1,i)%mod*C((n-i)>>1,n-i)%mod)%mod;
	}
	else	if(task==1)
		ans=Catalan(n>>1)%mod;
	else	if(task==2)
	{
		n>>=1;
		f[0]=1;
		f[1]=4;
		for(int i=2;i<=n;i++)
			for(int j=1;j<=i;j++)
				f[i]=(f[i]+4*f[i-j]%mod*Catalan(j-1)%mod)%mod;
		ans=f[n]%mod;
	}
	else
	{
		for(int i=0;i<=n;i+=2)
			ans=(ans+C(i,n)*Catalan(i>>1)%mod*Catalan((n-i)>>1)%mod)%mod;
	}
	printf("%lld",ans%mod);
	return 0;
}

T4 大佬

题解

解题思路

暴力打法

这个题一看题面和题目，令人畏惧，但是细细读题后可以发现：好像就是个深搜，再一看数据范围，直接开码 （然后我们愉快的TLE40pts）。

code

正解

有一个十分重要的地方就是怼大佬与活下来是两个事。

然后我们就可以分别运算了：

DP最多天数

类似于背包 DP ，利用前面的更新现在的直接 +1 就好了，最后对于所有的 dp 值取 mod ，求出最大天数就好了。

void get_Day()
{
	for(int i=1;i<=n;i++)//枚举天数
		for(int j=a[i];j<=mc;j++)//枚举自己的自信
		{
			dp[i][j-a[i]]=max(dp[i][j-a[i]],dp[i-1][j]+1);
			int temp=min(mc,j-a[i]+w[i]);
			dp[i][temp]=max(dp[i][temp],dp[i-1][j]);
		}
	for(int i=1;i<=n;i++)
		for(int j=1;j<=mc;j++)
			day=max(day,dp[i][j]);
}

BFS求二元组(d,f)

二元组 \((d,f)\) 表示第 d 天 \((d<D)\) 并且此时的 \(F=f\) ，运算的过程中需要去重，用 Hash 或者 map 可以很好的解决这个问题这里给出 map 做法。

队列的数组三维分别表示: 天数， L ，F，对于大于上面求的D，直接跳过，其他的枚举并更新 L 和 F 入队就好了，然后用一个 S1 数组储存所有的二元组。

void get_Dui()
{
	int head=1,tail=0;
	q[++tail]=make_pair(1,make_pair(0,1));
	a1[make_pair(1,1)]=1;
	while(head<=tail)
	{
		pair<int,pair<int,int> > temp;
		temp=q[head++];
		if(temp.first>=day)
			continue;
		int da=temp.first,l=temp.second.first,f=temp.second.second;
		q[++tail]=make_pair(da+1,make_pair(l+1,f));
		a1[make_pair(da+1,f)]=1;
		if(l>1&&l*f<=mxc&&!a1[make_pair(da+1,l*f)])
		{
			int new_f=l*f;
			q[++tail]=make_pair(da+1,make_pair(l,new_f));
			a1[make_pair(da+1,new_f)]=1;
			s1[++cnt]=make_pair(da+1,new_f);
		}
	}
}

算法主体

显然，可以怼没大佬自信值的情况有三种：

1. 一次都不怼，仅用 1 操作消磨他并且 \(C_i\le D\) 。
2. 只怼一次大佬，剩下的拿 1 来凑，这是需要有一个二元组 \((d,f)\) 满足 \(f\le C_i\) ,并且 \(f+D-d\ge C_i\)
3. 怼两次大佬，两次分别为 \((d_1,f_1)\) 和 \((d_2,f_2)\) 并且满足\(f_1+f_2 \le C_i\) 和 \(f_1+f_2-d_1-d_2+D \ge C_i\)。
   
   诚然，对于同一个 \(f\) 只有最小的 \(d\) 是最优的，因此我们只需要对于每一个 \(f\) 保存最小的 \(d\) 就好了， map 有一次正好的满足了这个条件（那还用Hash干嘛）,然后我们双向指针扫一下，再判断一小下就可以过掉此题了。

题目对于各项要求比较严格，具体实现细节见代码。

code

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e2+10,M=3e6+10,INF=1e9;//注意数组大小
int n,m,mc,mxc,a[N],w[N],c[25];
int tot,cnt,day,dp[N][N];
pair<int,int> s1[M],s2[M];
pair<int,pair<int,int> > q[M];//day l f
map<pair<int,int>,int> a1;
map<int,bool> a2;
void get_Day()//求出最大的day
{
	for(int i=1;i<=n;i++)//类似于背包dp
		for(int j=a[i];j<=mc;j++)
		{
			dp[i][j-a[i]]=max(dp[i][j-a[i]],dp[i-1][j]+1);
			int temp=min(mc,j-a[i]+w[i]);
			dp[i][temp]=max(dp[i][temp],dp[i-1][j]);
		}
	for(int i=1;i<=n;i++)//取最值
		for(int j=1;j<=mc;j++)
			day=max(day,dp[i][j]);
}
void get_Dui()//求二元组(d,f)
{
	int head=1,tail=0;
	q[++tail]=make_pair(1,make_pair(0,1));
	a1[make_pair(1,1)]=1;
	while(head<=tail)
	{
		pair<int,pair<int,int> > temp;
		temp=q[head++];
		if(temp.first>=day)
			continue;
		int da=temp.first,l=temp.second.first,f=temp.second.second;
		q[++tail]=make_pair(da+1,make_pair(l+1,f));
		a1[make_pair(da+1,f)]=1;
		if(l>1&&l*f<=mxc&&!a1[make_pair(da+1,l*f)])
		{
			int new_f=l*f;
			q[++tail]=make_pair(da+1,make_pair(l,new_f));
			a1[make_pair(da+1,new_f)]=1;
			s1[++cnt]=make_pair(da+1,new_f);
		}
	}
}
bool comp(pair<int ,int > x,pair<int ,int > y)//重新定义sort排序规则
{
	if(x.second==y.second)
		return x.first<y.first;
	return x.second<y.second;
}
#undef int
int main()
{
	#define int register long long
	#define ll long long
	scanf("%lld%lld%lld",&n,&m,&mc);
	for(int i=1;i<=n;i++)
		scanf("%lld",&a[i]);
	for(int i=1;i<=n;i++)
		scanf("%lld",&w[i]);
	for(int i=1;i<=m;i++)
	{
		scanf("%lld",&c[i]);
		mxc=max(mxc,c[i]);
	}
	get_Day();
	get_Dui();
	sort(s1+1,s1+cnt+1,comp);
	for(int i=1;i<=cnt;i++)
		if(!a2[s1[i].second])
		{
			a2[s1[i].second]=true;
			s2[++tot]=s1[i];
		}
	for(int k=1;k<=m;k++)
	{
		if(c[k]<=day)//一次也不怼
		{
			printf("1\n");
			continue;
		}
		bool vis=false;
		int pos=1;
		for(int i=tot;i>=1;i--)
		{
			int da=s2[i].first,f=s2[i].second;
			if(f<=c[k]&&day-da+f>=c[k])
			{
				vis=true;
				break;
			}
			int maxn=-INF;
			while(pos<=tot&&f+s2[pos].second<=c[k])
			{
				maxn=max(maxn,s2[pos].second-s2[pos].first);//如果是int，应该把+f卸载循环里不然会爆掉
				pos++;
			}
			if(f-da+maxn>=c[k]-day)//判断符合条件
			{
				vis=true;
				break;
			}
		}
		printf("%d\n",vis?1:0);
	}
	return 0;
}