Flink Exactly-once 实现原理解析

关注公众号：大数据技术派，回复"资料"，领取1024G资料。

这一课时我们将讲解 Flink “精确一次”的语义实现原理，同时这也是面试的必考点。

Flink 的“精确一次”处理语义是，Flink 提供了一个强大的语义保证，也就是说在任何情况下都能保证数据对应用产生的效果只有一次，不会多也不会少。

那么 Flink 是如何实现“端到端的精确一次处理”语义的呢？

背景

通常情况下，流式计算系统都会为用户提供指定数据处理的可靠模式功能，用来表明在实际生产运行中会对数据处理做哪些保障。一般来说，流处理引擎通常为用户的应用程序提供三种数据处理语义：最多一次、至少一次和精确一次。

最多一次（At-most-Once）：这种语义理解起来很简单，用户的数据只会被处理一次，不管成功还是失败，不会重试也不会重发。

至少一次（At-least-Once）：这种语义下，系统会保证数据或事件至少被处理一次。如果中间发生错误或者丢失，那么会从源头重新发送一条然后进入处理系统，所以同一个事件或者消息会被处理多次。

精确一次（Exactly-Once）：表示每一条数据只会被精确地处理一次，不多也不少。

Exactly-Once 是 Flink、Spark 等流处理系统的核心特性之一，这种语义会保证每一条消息只被流处理系统处理一次。“精确一次” 语义是 Flink 1.4.0 版本引入的一个重要特性，而且，Flink 号称支持“端到端的精确一次”语义。

在这里我们解释一下“端到端（End to End）的精确一次”，它指的是 Flink 应用从 Source 端开始到 Sink 端结束，数据必须经过的起始点和结束点。Flink 自身是无法保证外部系统“精确一次”语义的，所以 Flink 若要实现所谓“端到端（End to End）的精确一次”的要求，那么外部系统必须支持“精确一次”语义；然后借助 Flink 提供的分布式快照和两阶段提交才能实现。

分布式快照机制

我们在之前的课程中讲解过 Flink 的容错机制，Flink 提供了失败恢复的容错机制，而这个容错机制的核心就是持续创建分布式数据流的快照来实现。

同 Spark 相比，Spark 仅仅是针对 Driver 的故障恢复 Checkpoint。而 Flink 的快照可以到算子级别，并且对全局数据也可以做快照。Flink 的分布式快照受到 Chandy-Lamport 分布式快照算法启发，同时进行了量身定做，有兴趣的同学可以搜一下。

Barrier

Flink 分布式快照的核心元素之一是 Barrier（数据栅栏），我们也可以把 Barrier 简单地理解成一个标记，该标记是严格有序的，并且随着数据流往下流动。每个 Barrier 都带有自己的 ID，Barrier 极其轻量，并不会干扰正常的数据处理。

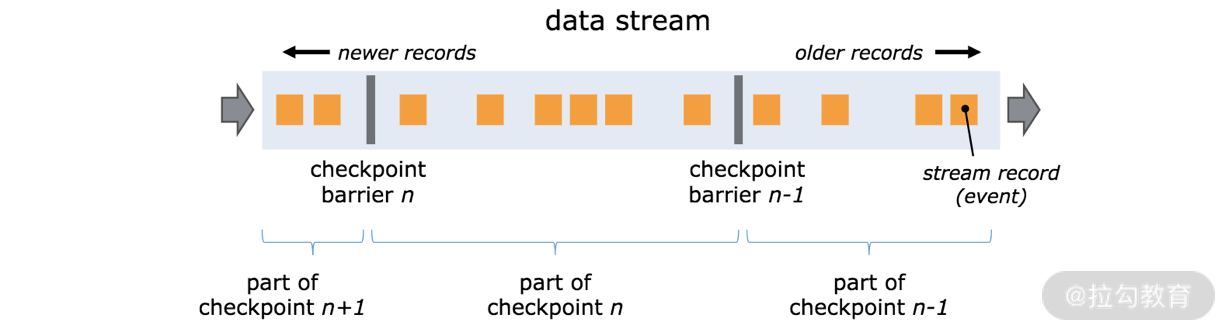
如上图所示，假如我们有一个从左向右流动的数据流，Flink 会依次生成 snapshot 1、 snapshot 2、snapshot 3……Flink 中有一个专门的“协调者”负责收集每个 snapshot 的位置信息，这个“协调者”也是高可用的。

Barrier 会随着正常数据继续往下流动，每当遇到一个算子，算子会插入一个标识，这个标识的插入时间是上游所有的输入流都接收到 snapshot n。与此同时，当我们的 sink 算子接收到所有上游流发送的 Barrier 时，那么就表明这一批数据处理完毕，Flink 会向“协调者”发送确认消息，表明当前的 snapshot n 完成了。当所有的 sink 算子都确认这批数据成功处理后，那么本次的 snapshot 被标识为完成。

这里就会有一个问题，因为 Flink 运行在分布式环境中，一个 operator 的上游会有很多流，每个流的 barrier n 到达的时间不一致怎么办？这里 Flink 采取的措施是：快流等慢流。

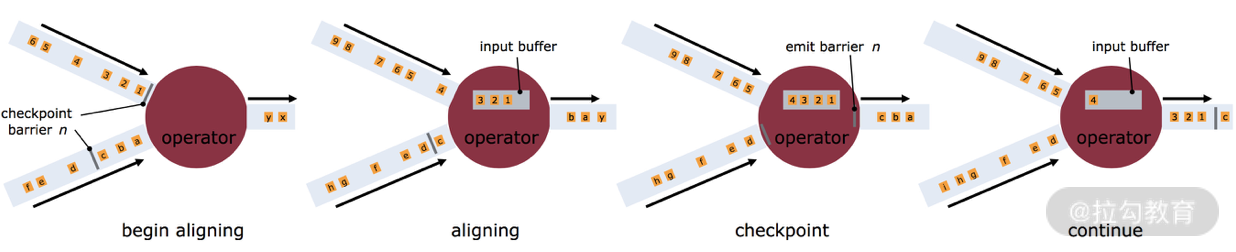
拿上图的 barrier n 来说，其中一个流到的早，其他的流到的比较晚。当第一个 barrier n到来后，当前的 operator 会继续等待其他流的 barrier n。直到所有的barrier n 到来后，operator 才会把所有的数据向下发送。

异步和增量

按照上面我们介绍的机制，每次在把快照存储到我们的状态后端时，如果是同步进行就会阻塞正常任务，从而引入延迟。因此 Flink 在做快照存储时，可采用异步方式。

此外，由于 checkpoint 是一个全局状态，用户保存的状态可能非常大，多数达 G 或者 T 级别。在这种情况下，checkpoint 的创建会非常慢，而且执行时占用的资源也比较多，因此 Flink 提出了增量快照的概念。也就是说，每次都是进行的全量 checkpoint，是基于上次进行更新的。

两阶段提交

上面我们讲解了基于 checkpoint 的快照操作，快照机制能够保证作业出现 fail-over 后可以从最新的快照进行恢复，即分布式快照机制可以保证 Flink 系统内部的“精确一次”处理。但是我们在实际生产系统中，Flink 会对接各种各样的外部系统，比如 Kafka、HDFS 等，一旦 Flink 作业出现失败，作业会重新消费旧数据，这时候就会出现重新消费的情况，也就是重复消费。

针对这种情况，Flink 1.4 版本引入了一个很重要的功能：两阶段提交，也就是 TwoPhaseCommitSinkFunction。两阶段搭配特定的 source 和 sink（特别是 0.11 版本 Kafka）使得“精确一次处理语义”成为可能。

在 Flink 中两阶段提交的实现方法被封装到了 TwoPhaseCommitSinkFunction 这个抽象类中，我们只需要实现其中的beginTransaction、preCommit、commit、abort 四个方法就可以实现“精确一次”的处理语义，实现的方式我们可以在官网中查到：

beginTransaction，在开启事务之前，我们在目标文件系统的临时目录中创建一个临时文件，后面在处理数据时将数据写入此文件；
preCommit，在预提交阶段，刷写（flush）文件，然后关闭文件，之后就不能写入到文件了，我们还将为属于下一个检查点的任何后续写入启动新事务；
commit，在提交阶段，我们将预提交的文件原子性移动到真正的目标目录中，请注意，这会增加输出数据可见性的延迟；

abort，在中止阶段，我们删除临时文件。

Flink-Kafka Exactly-once

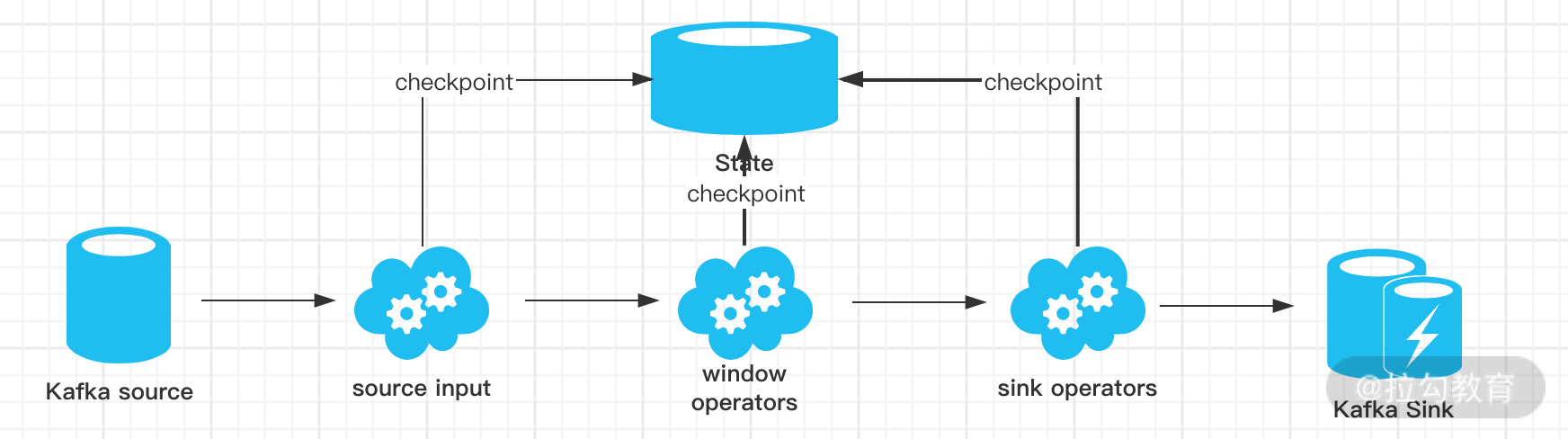
如上图所示，我们用 Kafka-Flink-Kafka 这个案例来介绍一下实现“端到端精确一次”语义的过程，整个过程包括：

从 Kafka 读取数据
窗口聚合操作
将数据写回 Kafka

整个过程可以总结为下面四个阶段：

一旦 Flink 开始做 checkpoint 操作，那么就会进入 pre-commit 阶段，同时 Flink JobManager 会将检查点 Barrier 注入数据流中；
当所有的 barrier 在算子中成功进行一遍传递，并完成快照后，则 pre-commit 阶段完成；
等所有的算子完成“预提交”，就会发起一个“提交”动作，但是任何一个“预提交”失败都会导致 Flink 回滚到最近的 checkpoint；
pre-commit 完成，必须要确保 commit 也要成功，上图中的 Sink Operators 和 Kafka Sink 会共同来保证。

现状

目前 Flink 支持的精确一次 Source 列表如下表所示，你可以使用对应的 connector 来实现对应的语义要求：

数据源	语义保证	备注
Apache Kafka	exactly once	需要对应的 Kafka 版本
AWS Kinesis Streams	exactly once
RabbitMQ	at most once (v 0.10) / exactly once (v 1.0)
Twitter Streaming API	at most once
Collections	exactly once
Files	exactly once
Sockets	at most once

如果你需要实现真正的“端到端精确一次语义”，则需要 sink 的配合。目前 Flink 支持的列表如下表所示：

写入目标	语义保证	备注
HDFS rolling sink	exactly once	依赖 Hadoop 版本
Elasticsearch	at least once
Kafka producer	at least once / exactly once	需要 Kafka 0.11 及以上
Cassandra sink	at least once / exactly once	幂等更新
AWS Kinesis Streams	at least once
File sinks	at least once
Socket sinks	at least once
Standard output	at least once
Redis sink	at least once

总结

由于强大的异步快照机制和两阶段提交，Flink 实现了“端到端的精确一次语义”，在特定的业务场景下十分重要，我们在进行业务开发需要语义保证时，要十分熟悉目前 Flink 支持的语义特性。

这一课时的内容较为晦涩，建议你从源码中去看一下具体的实现。