Ng第二课：单变量线性回归(Linear Regression with One Variable)

二、单变量线性回归(Linear Regression with One Variable)

2.1 模型表示

2.2 代价函数

2.3 代价函数的直观理解

2.4 梯度下降

2.5 梯度下降的直观理解

2.6 梯度下降的线性回归

2.7 接下来的内容

2.1 模型表示

之前的房屋交易问题为例，假使我们回归问题的训练集（Training Set）如下表所示：

我们将要用来描述这个回归问题的标记如下:

m 代表训练集中实例的数量

x 代表特征/输入变量

y 代表目标变量/输出变量

(x,y) 代表训练集中的实例

(x(i),y(i)) 代表第 i 个观察实例

h 代表学习算法的解决方案或函数也称为假设（hypothesis）

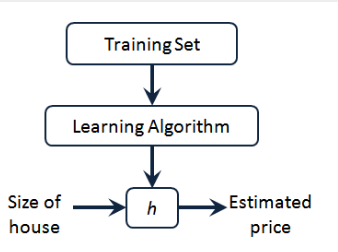
因而，要解决房价预测问题，我们实际上是要将训练集“喂”给我们的学习算法，进而学习得到一个假设 h，然后把我们要预测的房屋的尺寸作为输入变量输入给 h，预测出该房屋的交易价格作为输出变量输出为结果。对于这个房价预测问题，一种可能的表达方式为：

，因为只含有一个特征/输入变量，因此这样的问题叫作单变量线性回归问题。

2.2 代价函数

我们现在要做的便是为我们的模型选择合适的参数（parameters）θ0 和 θ1，在房价问题这个例子中便是直线的斜率和在 y 轴上的截距。

我们选择的参数决定了我们得到的直线相对于我们的训练集的准确程度，模型所预测的值与训练集中实际值之间的差距（下图中蓝线所指部分）就是建模误差（modeling error）。

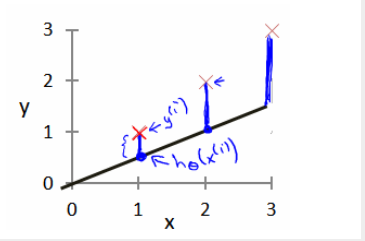
我们的目标便是选择出可以使得建模误差的平方和能够最小的模型参数。即使得代价函数

我们绘制一个等高线图，三个坐标分别为 θ0 和 θ1 和 J(θ0,θ1)：

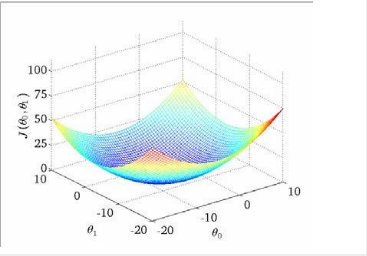
则可以看出在三维空间中存在一个使得 J(θ0,θ1)最小的点。

2.3 代价函数的直观理解

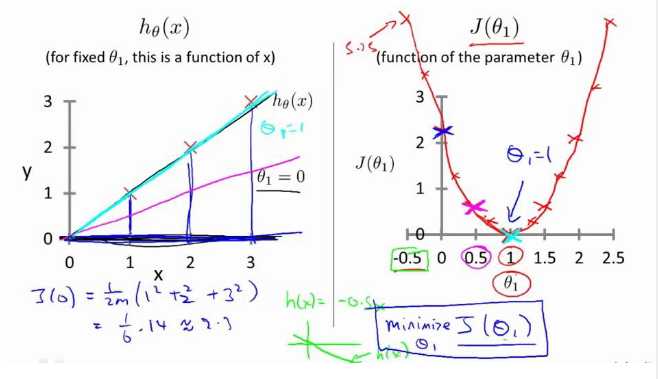
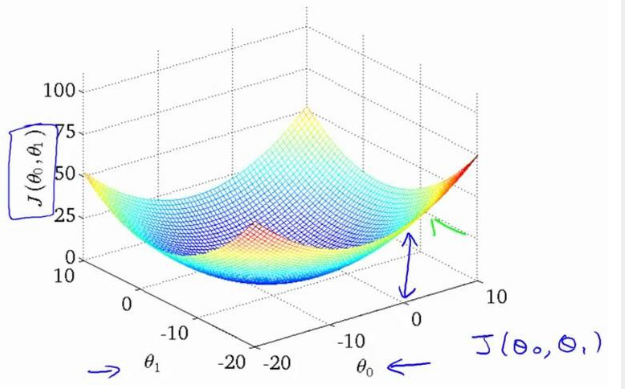
图1是不考虑θ_0、θ₁时J(0)为常数，图2是当只考虑θ₁时代价函数J(θ₁)的情况，图3是θ_0、θ₁都考虑时J(θ_0，θ₁)的情况。

代价函数的样子:

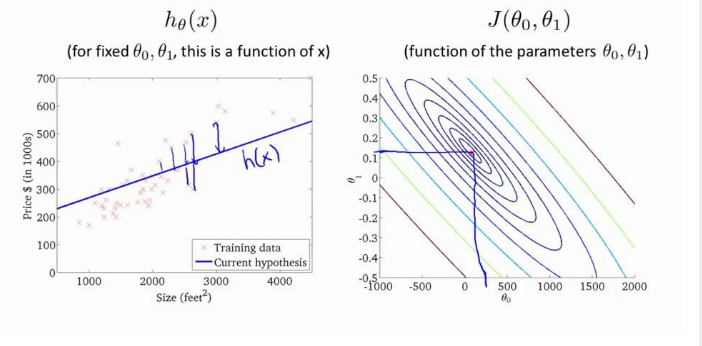
图1是固定的θ_0、θ_1，图2是参数的θ_0、θ₁

2.4 梯度下降的直观理解

梯度下降算法如下：

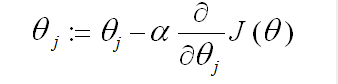
梯度下降的原理描述：首先对随机赋初值，减后值改变再带进去，使得按梯度下降最快的方向进行，一直迭代下去最终会得到局部最小值，即上式

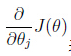表示最陡的那个方向，α 是学习率（learning rate）(步长)也就是说每次向下降最快的方向走多远。α过大时，有可能越过最小值，当α过小时，容易造成迭代次数较多收敛速度较慢。

2.5 梯度下降的线性回归

梯度下降算法和线性回归算法比较如图：

对之前的线性回归问题运用梯度下降法，关键在于求出代价函数的导数，即：

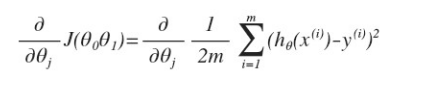
j=0 时：

j=1 时：

则算法改写成：

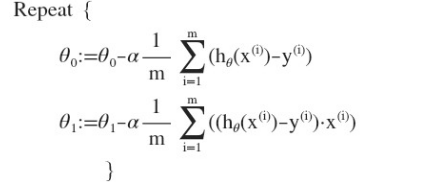
2.6 接下来的内容

在接下来的一组视频中，我会对将用到的线性代数进行一个快速的复习回顾。

通过它们，你可以实现和使用更强大的线性回归模型。事实上，线性代数不仅仅在线性回归中应用广泛，它其中的矩阵和向量将有助于帮助我们实现之后更多的机器学习模型，并在计算上更有效率。正是因为这些矩阵和向量提供了一种有效的方式来组织大量的数据，特别是当我们处理巨大的训练集时。

事实上，为了实现机器学习算法，我们只需要一些非常非常基础的线性代数知识。具体来说，为了帮助你判断是否有需要学习接下来的一组视频，我会讨论什么是矩阵和向量，谈谈如何加、减、乘矩阵和向量，讨论逆矩阵和转置矩阵的概念。