p1 批梯度下降算法

（蓝色字体：批注；绿色背景：需要注意的地方；橙色背景是问题）

一，机器学习分类

二，梯度下降算法：2.1模型   2.2代价函数   2.3 梯度下降算法

一，机器学习分类

无监督学习和监督学习

无监督学习主要有聚类算法（例题：鸡尾酒会算法）根据数据中的变量关系来将数据进行分类

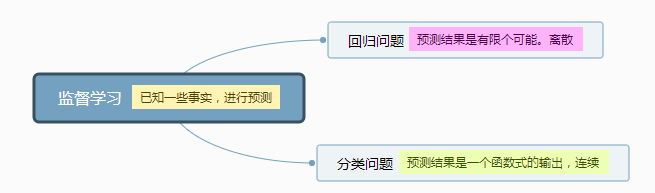
其中分类算法，可以根据一个特征来分类，多个特征分类更加准确

二，多元回归问题

2.1 模型定义：

　　

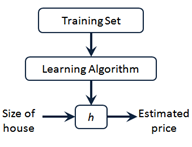
m代表训练集中实例的数量

x  代表特征或者输入变量 （x是一个向量，可以有很多特征）

y  代表目标变量/输出变量（y也有可能是一个特征）

（x,y）代表训练集中的实例（训练样本）

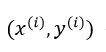代表第 i个观察实例（训练样本）

h :假设。

2.2 　　代价函数

　　定义：衡量  模型预测出来的值h(θ)与真实值y之间的差异  的函数。（如果有多个样本，则可以将所有代价函数的取值求均值，记做J(θ)。）

　　用处：我们用代价函数是为了训练参数θ，利用代价函数衡量θ的好坏。从而得到最符合训练集的模型

　　性质：

• 对于每种算法来说，代价函数不是唯一的；
• 代价函数的自变量是θ，而假设函数h的自变量是x。
• 总的代价函数J(θ)可以用来评价模型的好坏，代价函数越小说明模型和参数越符合训练样本(x, y)；
• J(θ)是一个标量；
• 选择代价函数时，最好挑选对参数θ可微的函数

　　理想情况下，当我们取到代价函数J的最小值时，就得到了最优的参数θ，记为：minθJ(θ)。例如，J(θ) = 0，表示我们的模型完美的拟合了观察的数据，没有任何误差。

　　参考：https://www.cnblogs.com/Belter/p/6653773.html?utm_source=itdadao&utm_medium=referral

　　（在训练过程中：选取模型，这个过程只是一个模型比如是多元多次函数，指数函数等，确定参数个数；给参数一个初始值；然后利用训练集训练；使代价函数收敛于最小值，即确定参数）

　　代价函数有均方误差函数，交叉熵函数等

2.3 批梯度下降算法

对于二元线性问题：

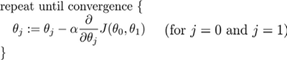
实现梯度下降算法的微妙之处是，在这个表达式中，需要同时更新 和Θ1，Θ0：

• 这里的Θ是一个标量，减法并不能代表矢量运算，梯度下降里面的偏导数现在只是一个正负的区别，并不表示一个方向。因为梯度的定义是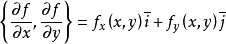：。梯度是一个向量。这这里只是梯度的一个坐标。所以每一次参数更新都是同时更新两个
• 这里的同步更新是很重要的，因为不同步，两个参数会前后影响
• 这里的参数更新用相减的形式是为了更靠近J最低点的地方，就是让J更快速靠近最低点。而且此时的更新不再沿着函数变化，而是沿着每一个地方的切线。

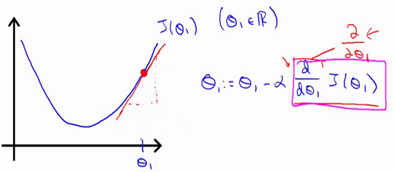
对于二元问题，这里的 α 是我们切线上纵坐标变化值Δy。这里我们不用改变α ，最终由偏导数来控制大小然后实现收敛。

梯度下降算法是根据当前点找偏导数最小的方向然后更改点的位置，所以算法看不见最小值，只能找到这个方向进行参数的训练，所以要注意当学习率比较大时，如果代价函数不是凸函数就很有可能迭代到离我们的最小值很远的局部最小值点。而且对于多维函数，偏导的方向并不向一维一样只能在正负方向，偏导方向可能是四面八方。

 对于多元线性问题：

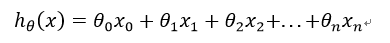其中x0=1（为了方便运算添加了x0）

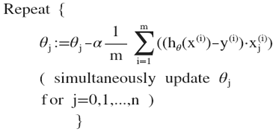
计算所有的预测结果后，再给所有的参数一个新的值，如此循环直到收敛。这里注意也是同时更新