LCT做题笔记
最近几天打算认真复习LCT，毕竟以前只会板子。正好也可以学点新的用法，这里就用来写做题笔记吧。这个分类比较混乱，主要看感觉，不一定对；
维护森林的LCT
就是最普通，最一般那种的LCT啦。这类题目往往就是用LCT维护森林，从而快速的实现一些链上操作；其中，某些题只是维护一棵形态固定的树，用树剖也可以做，复杂度 $n\log^2n$，如果使用LCT则变成了 $n\log n$；有的题目涉及断边连边，就必须使用LCT了。这次复习做的前几道题都属于这种，这几道题的难点其实不在LCT上，只要会敲模板就OK了，可以稍微练习码力。正好这次就顺便把以前做过的题一起整理一下吧~一个可能会一时糊涂理解不了的地方：当我说“每个点记录某某信息时”，指的是维护Splay上的子树信息，但是由于Splay本质上是在维护树链，所以split一段路径后，splay的根节点记录的就是树链信息了。
[模板]Link Cut Tree
题意概述：断边加边，修改点权，询问路径异或和；
是一道小清新的模板题呢，只用到了一些基础的操作，没有区间修改这类稍微复杂的东西。
# include <cstdio>
# include <iostream>
# include <cstring>
# include <string>
# define R register int
# define getchar() (S==T&&(T=(S=BB)+fread(BB,,<<,stdin),S==T)?EOF:*S++) using namespace std; const int maxn=;
int n,m,opt,x,y;
int v[maxn],ch[maxn][],f[maxn],sta[maxn],Tp,s[maxn],rev[maxn];
char BB[ << ], *S = BB, *T = BB; int read()
{
R x=;
char c=getchar();
while (!isdigit(c)) c=getchar();
while (isdigit(c)) x=(x<<)+(x<<)+(c^),c=getchar();
return x;
} bool rt (int x) { return (ch[ f[x] ][]==x||ch[ f[x] ][]==x); } //x是所在splay的根吗？
void update (int x) { s[x]=v[x]^s[ ch[x][] ]^s[ ch[x][] ]; }
void swp (int x) { rev[x]^=; swap(ch[x][],ch[x][]); }
void pushdown (int x)
{
if(rev[x]==) return ;
if(ch[x][]) swp(ch[x][]);
if(ch[x][]) swp(ch[x][]);
rev[x]=;
} void rotate (int x)
{
int fx=f[x],ff=f[fx],k=(ch[fx][]==x),t=ch[x][k^];
if(rt(fx)) ch[ff][ ch[ff][]==fx ]=x;
ch[fx][k]=t,ch[x][k^]=fx,f[fx]=x,f[x]=ff;
if(t) f[t]=fx;
update(fx);
} void splay (int x) //把x转到自己所在splay的根上去
{
Tp=,sta[++Tp]=x;
int y=x;
while(rt(y)) sta[++Tp]=(y=f[y]);
for (R i=Tp;i>=;--i) pushdown(sta[i]);
int fx,ff;
while(rt(x))
{
fx=f[x],ff=f[fx];
if(rt(fx)) rotate(((ch[fx][]==x)!=(ch[ff][]==fx))?x:fx);
rotate(x);
}
update(x);
} int ws (int x) { return (ch[ f[x] ][]==x); } //x是父亲的哪个孩子？
void access (int x)
{
for (R y=;x;y=x,x=f[x])
splay(x),ch[x][]=y,update(x);
} void change_root (int x) { access(x); splay(x); swp(x); }
int find (int x)
{
access(x),splay(x);
while(ch[x][]) pushdown(x),x=ch[x][];
return x;
} void link (int x,int y)
{
change_root(x);
if(find(y)!=x) f[x]=y;
} void cut (int x,int y)
{
change_root(x);
if(find(y)!=x||f[x]!=y||ch[x][]) return ;
f[x]=ch[y][]=;
update(y);
} void split (int x,int y)
{
change_root(x);
access(y),splay(y);
} void write (int x)
{
if(x>=) write(x/);
putchar(x%+'');
} int main()
{
n=read(),m=read();
for (R i=;i<=n;++i) v[i]=read();
for (R i=;i<=m;++i)
{
opt=read(),x=read(),y=read();
if(opt==) split(x,y),write(s[y]),putchar('\n');
else if(opt==) link(x,y);
else if(opt==) cut(x,y);
else if(opt==) splay(x),v[x]=y;
}
return ;
}
Link Cut Tree
洞穴勘探
题意概述：断边加边，询问连通性；
这道题用到了findroot来判断连通性。不过这是2008年的题，那时候LCT还没有特别普及吧，不知道当年的标算是什么？
# include <cstdio>
# include <iostream>
# include <cstring>
# include <string>
# define R register int using namespace std; const int maxn=;
int n,m,x,y,F[maxn],ch[maxn][],t[maxn],st[maxn],Tp;
char c[]; inline bool isnt_rt (int x) { return ch[ F[x] ][]==x||ch[ F[x] ][]==x; }
inline void rev (int x) { swap(ch[x][],ch[x][]); t[x]^=; }
inline void pushdown (int x) { if(t[x]) rev(ch[x][]),rev(ch[x][]),t[x]=; }
inline int D (int x) { return ch[ F[x] ][]==x; } inline void rotate (int x)
{
int f=F[x],g=F[f],dx=D(x),df=D(F[x]);
int k=ch[x][dx^];
if(isnt_rt(f)) ch[g][df]=x;
ch[f][dx]=k;
ch[x][dx^]=f;
if(k) F[k]=f;
F[f]=x; F[x]=g;
} inline void splay (int x)
{
// printf("splay(%d)\n",x);
int t=x,f,g;
st[++Tp]=t;
while (isnt_rt(t)) st[++Tp]=F[t],t=F[t];
while (Tp) pushdown(st[Tp]),Tp--;
while (isnt_rt(x))
{
f=F[x],g=F[f];
if(isnt_rt(f))
{
if(D(x)==D(f)) rotate(f);
else rotate(x);
}
rotate(x);
}
} inline void access (int x)
{
// printf("access(%d)\n",x);
for (int y=;x;y=x,x=F[x])
splay(x),ch[x][]=y;
} inline void makeroot (int x)
{
// printf("makeroot(%d)\n",x);
access(x);
splay(x);
rev(x);
} inline int findroot (int x)
{
// printf("findroot(%d)\n",x);
access(x),splay(x);
while(ch[x][]) pushdown(x),x=ch[x][];
splay(x);
return x;
} inline void link (int x,int y)
{
// printf("link(%d %d)\n",x,y);
makeroot(x);
if(findroot(y)!=x) F[x]=y;
access(y);
} inline void cut (int x,int y)
{
// printf("cut(%d %d)\n",x,y);
makeroot(x);
access(y);
splay(y);
F[x]=,ch[y][]=;
} int main()
{
scanf("%d%d",&n,&m);
for (R i=;i<=m;++i)
{
scanf("%s",c+);
scanf("%d%d",&x,&y);
if (c[]=='Q')
{
if(findroot(x)==findroot(y)) printf("Yes\n");
else printf("No\n");
}
else if (c[]=='C')
link(x,y);
else if (c[]=='D')
cut(x,y);
}
return ;
}
洞穴勘测
Tree II
题意概述：需要支持路径乘，路径加，断边加边，询问路径和；$n<=10^5$
其实还是...比较简单的吧...就是在普通的LCT上打打标记（乘法，翻转，加法），维护一些信息（子树和，子树大小），稍微有点难写。不要忘了Splay时标记要从上往下放！一个小坑：模数虽小，乘法时也要开longlong。
# include <cstdio>
# include <iostream>
# include <cstring>
# include <string>
# define R register int
# define ll unsigned int using namespace std; const int maxn=;
const int mod=;
int n,q,x,y,db;
int ch[maxn][],f[maxn],r[maxn],st[maxn];
ll da[maxn],dm[maxn],s[maxn],siz[maxn],v[maxn];
char opt[]; int read()
{
R x=;
char c=getchar();
while (!isdigit(c)) c=getchar();
while (isdigit(c)) x=(x<<)+(x<<)+(c^),c=getchar();
return x;
} bool isntroot (int x) { return ch[ f[x] ][]==x||ch[ f[x] ][]==x; } int D (int x) { return ch[ f[x] ][]==x; } void update (int x)
{
int l=ch[x][],r=ch[x][];
siz[x]=(siz[l]+siz[r]+)%mod;
s[x]=(s[l]+s[r]+v[x])%mod;
} inline void turn (int x)
{
r[x]^=;
swap(ch[x][],ch[x][]);
} inline void rev (int x)
{
r[x]=;
if(ch[x][]) turn(ch[x][]);
if(ch[x][]) turn(ch[x][]);
} inline void pushdown (int x)
{
if(dm[x]==&&da[x]==&&r[x]==) return;
if(r[x]) rev(x);
int l=ch[x][],r=ch[x][];
if(l)
{
v[l]=(v[l]*dm[x]+da[x])%mod;
s[l]=(s[l]*dm[x]+siz[l]*da[x])%mod;
dm[l]=dm[l]*dm[x]%mod;
da[l]=(da[l]*dm[x]+da[x])%mod;
}
if(r)
{
v[r]=(v[r]*dm[x]+da[x])%mod;
s[r]=(s[r]*dm[x]+siz[r]*da[x])%mod;
dm[r]=dm[r]*dm[x]%mod;
da[r]=(da[r]*dm[x]+da[x])%mod;
}
dm[x]=; da[x]=;
} void rotate (int x)
{
if(db) printf("rotate(%d)\n",x);
int F=f[x],g=f[F],d=D(x),df=D(F);
pushdown(F); pushdown(x);
int k=ch[x][d^];
ch[F][d]=k;
ch[x][d^]=F;
if(isntroot(F)) ch[g][df]=x;
if(k)f[k]=F; f[F]=x; f[x]=g;
update(F); update(x);
} void splay (int x)
{
if(db) printf("splay(%d)\n",x);
int y=x,tp=;
st[++tp]=x;
while(isntroot(y)) st[++tp]=f[y],y=f[y];
while(tp) pushdown(st[tp]),tp--;
while(isntroot(x))
{
int F=f[x],g=f[g];
if(!isntroot(F)) rotate(x);
else if(D(x)==D(F)) rotate(F),rotate(x);
else rotate(x),rotate(x);
}
} void access (int x)
{
if(db) printf("access(%d)\n",x);
int y=;
while(x)
{
splay(x);
ch[x][]=y;
update(x);
y=x; x=f[x];
}
} void make_root (int x)
{
if(db) printf("make_root(%d)\n",x);
access(x);
splay(x);
turn(x);
} void spilt (int x,int y)
{
if(db) printf("spilt(%d,%d)\n",x,y);
make_root(x);
access(y);
splay(y);
} void link (int x,int y)
{
if(db) printf("link(%d,%d)\n",x,y);
make_root(x);
f[x]=y;
} void cut (int x,int y)
{
if(db) printf("cut(%d,%d)\n",x,y);
spilt(x,y);
f[x]=; ch[y][]=;
update(y);
} void mul (int x,int y,int c)
{
c%=mod;
spilt(x,y);
v[y]=v[y]*c%mod; s[y]=s[y]*c%mod;
da[y]=da[y]*c%mod; dm[y]=dm[y]*c%mod;
} void add (int x,int y,int c)
{
c%=mod;
spilt(x,y);
v[y]=(v[y]+c)%mod; s[y]=(s[y]+siz[y]*c)%mod;
da[y]=(da[y]+c)%mod;
} int main()
{
scanf("%d%d",&n,&q);
for (R i=;i<=n;++i)
v[i]=siz[i]=s[i]=dm[i]=;
for (R i=;i<n;++i)
{
x=read(),y=read();
link(x,y);
}
for (R i=;i<=q;++i)
{
int c;
scanf("%s",opt);
if(opt[]=='+')
{
x=read(),y=read(),c=read();
add(x,y,c);
}
else if(opt[]=='-')
{
x=read(),y=read();
cut(x,y);
x=read(),y=read();
link(x,y);
}
else if(opt[]=='*')
{
x=read(),y=read(),c=read();
mul(x,y,c);
}
else if(opt[]=='/')
{
x=read(),y=read();
spilt(x,y);
printf("%u\n",s[y]);
}
}
return ;
}
Tree II
弹飞绵羊
这道题概述题意后就没啥好做的啦。其实就是每个点向被弹到的点连边，构成一个森林结构，询问时就查一下这个点的深度，是不是很简单呢。
# include <cstdio>
# include <iostream>
# define R register int using namespace std; const int maxn=;
int n,m,t[maxn],opt,F[maxn],ch[maxn][],siz[maxn],x,y; inline int D (int x) { return ch[ F[x] ][]==x; }
inline bool isnt_root (int x) { return ch[ F[x] ][]==x||ch[ F[x] ][]==x; }
inline void update (int x) { siz[x]=siz[ ch[x][] ]+siz[ ch[x][] ]+; }
inline void rotate (int x)
{
int f=F[x],g=F[f],dx=D(x),df=D(f);
int k=ch[x][dx^];
ch[f][dx]=k;
if(isnt_root(f)) ch[g][df]=x;
F[f]=x,F[k]=f;
ch[x][dx^]=f;
F[x]=g;
update(f),update(x);
} inline void splay (int x)
{
while(isnt_root(x))
{
if(isnt_root(F[x]))
rotate((D(x)==D(F[x]))?F[x]:x);
rotate(x);
}
update(x);
}
inline void access (int x) { for (int y=;x;y=x,x=F[x]) splay(x),ch[x][]=y,update(x); } inline int read ()
{
R x=;
char c=getchar();
while (!isdigit(c)) c=getchar();
while (isdigit(c)) x=(x<<)+(x<<)+(c^),c=getchar();
return x;
} int main()
{
scanf("%d",&n);
for (R i=;i<=n;++i)
{
siz[i]=;
x=read();
if(i+x<=n) F[i]=i+x;
}
scanf("%d",&m);
for (R i=;i<=m;++i)
{
opt=read(),x=read();
x++;
if(opt==)
{
access(x),splay(x);
printf("%d\n",siz[x]);
}
else
{
scanf("%d",&y);
access(x),splay(x);
ch[x][]=F[ ch[x][] ]=;
if(x+y<=n) F[x]=x+y;
update(x);
}
}
return ;
}
弹飞绵羊
在美妙的数学王国中畅游
从这里开始难度开始加大了，然而似乎难度不在LCT上...
题意概述：给出一个动态加边删边的森林，每个点上有一个函数，是以下三种函数中的一种 $ax+b,sin(ax+b),e^{ax+b}$ ，$a,b$ 对于每个点不同。同时，也会有单点修改点上函数的操作；给出一些询问，询问对于某个 $x$ ，将它分别带入 $u$ 到 $v$ 的路径上所有函数所得函数值的和。
乍一看这道题很难，其实也确实不算简单。动态加边删边，明示LCT，现在的问题就是怎样快速的计算这些函数；经过观察，可以发现形如 $ax+b$ 的函数显然是很好合并的，这就启示我们把所有函数都变成多项式，因为多项式相加是可以把值相加的。往下翻题面，发现他给出了一个泰勒展开的式子，这证实了上面的猜想：对每个函数进行泰勒展开，用多项式来近似求这些函数值的和。由于多项式是可以合并的，这道题也就迎刃而解了；
在这里，我先把泰勒展开的式子写出来：
$\rm \sum_{i=0}^n\frac{f^{(i)}(x_0)(x-x_0)^i}{i!}$
显然，$ax+b$就不用泰勒展开了...$e^x,sin(x)$求导不算特别简单，但是基本上知道求导的同学也都知道这些公式吧...
$\rm (sin(x))'=cos(x),(cos(x))'=-sin(x)$ $\rm(e^x)'=e^x$
那么，$x_0$ 取多少比较合适呢？当然是0啦~，取0多方便啊，首先,$ax+b=b$ 这一点就方便很多，$ax+b-ax_0-b=ax$就更妙了，把 $a^i$ 直接乘进系数里，就可以得到关于 $x$ 的多项式啦；因为分母增长很快，而分子缩小得也很快，所以取前15项就可以完成要求咯。
三叉神经树
这题挺妙的，要稍微观察一下性质；
首先，改变一个输入，可能会被影响的只有从它到根这条路径上的点；如果路径上的某个点没有被影响，那么从它往上就更不会被影响了；再次观察，可以发现，一个输入从0->1，只会将从这里往上连续的一串1变成2，再往上一个数+1，其它的都不变；1->0，只会将从这里往上连续的一串2变成1，再往上一个数-1，其它的都不变；所以说，我们只需要在LCT的每个点上维护从这个点到根的路径上深度最小的非1点位置和非2点位置。区间+1/-1后，所有不是1的都变得不是2了，所有不是2的都变得不是1了，所以只需要交换这两个信息就可以维护了。这道题重在观察，只要这些性质都能看出来，写代码反而变得挺简单了。
# include <cstdio>
# include <iostream>
# include <queue>
# define R register int using namespace std; const int N=;
int n,q,x,x1,x2,x3;
int lk[N*],tf[N],d[N];
int ch[N][],f[N],sta[N];
int s[][N],a[N*];
int v[N],delta[N],rev[N]; int read()
{
int x=;
char c=getchar();
while (!isdigit(c)) c=getchar();
while (isdigit(c)) x=(x<<)+(x<<)+(c^),c=getchar();
return x;
} void update (int x)
{
for (R i=;i<=;++i)
{
s[i][x]=s[i][ ch[x][] ];
if(s[i][x]==&&v[x]!=i) s[i][x]=x;
if(s[i][x]==) s[i][x]=s[i][ ch[x][] ];
}
} void add (int x,int opt)
{
delta[x]+=opt; v[x]+=opt;
swap(s[][x],s[][x]);
} void pushdown (int x)
{
if(rev[x])
{
rev[x]=;
swap(ch[x][],ch[x][]);
if(ch[x][]) rev[ ch[x][] ]^=;
if(ch[x][]) rev[ ch[x][] ]^=;
}
if(delta[x])
{
int t=delta[x];
if(ch[x][]) add(ch[x][],t);
if(ch[x][]) add(ch[x][],t);
delta[x]=;
}
} bool isntroot (int x) { return (ch[ f[x] ][]==x||ch[ f[x] ][]==x); } int D (int x) { return ch[ f[x] ][]==x; } void rotate (int x)
{
int F=f[x],g=f[F];
int dx=D(x),df=D(F);
int k=ch[x][dx^];
ch[F][dx]=k;
ch[x][dx^]=F;
if(ch[g][df]==F) ch[g][df]=x;
if(k) f[k]=F; f[F]=x; f[x]=g;
update(F);
update(x);
} void splay (int x)
{
int y=x,tp=; sta[++tp]=x;
while(isntroot(y)) sta[++tp]=f[y],y=f[y];
for (R i=tp;i>=;--i) pushdown(sta[i]);
while(isntroot(x))
{
int t=f[x];
if(!isntroot(t)) rotate(x);
else if(D(t)==D(x)) rotate(t),rotate(x);
else rotate(x),rotate(x);
}
} void access (int x)
{
int y=;
while()
{
splay(x);
ch[x][]=y;
update(x);
y=x; x=f[x];
if(!x) return;
}
} void makeroot (int x)
{
access(x); splay(x);
rev[x]^=;
} void link (int x,int y) { makeroot(x); f[x]=y; } void split (int x,int y)
{
makeroot(x);
access(y);
splay(y);
} void topu()
{
queue<int> q;
for (R i=;i<=n;++i)
if(d[i]==) q.push(i);
int beg;
while(q.size())
{
beg=q.front(); q.pop();
if(beg==) return;
v[ tf[beg] ]+=(v[beg]>=);
d[ tf[beg] ]--;
if(d[ tf[beg] ]==) q.push(tf[ beg ]);
}
} int main()
{
n=read();
for (R i=;i<=n;++i)
{
x1=read(); x2=read(); x3=read(); d[i]=;
if(x1<=n) tf[x1]=i; else lk[x1-n]=i;
if(x2<=n) tf[x2]=i; else lk[x2-n]=i;
if(x3<=n) tf[x3]=i; else lk[x3-n]=i;
}
for (R i=;i<=*n+;++i)
{
a[i]=read();
v[ lk[i] ]+=a[i];
d[ lk[i] ]--;
}
topu();
for (R i=;i<=n;++i)
{
if(v[i]!=) s[][i]=i;
if(v[i]!=) s[][i]=i;
}
for (R i=;i<=n;++i)
link(i,tf[i]);
q=read();
for (R i=;i<=q;++i)
{
x=read(); x-=n; a[x]^=;
if(!a[x])
{
x=lk[x]; split(,x);
if(!s[][x])
{
splay(x);
add(x,-);
}
else
{
x=s[][x]; splay(x);
if(ch[x][]) add(ch[x][],-);
v[x]--; update(x);
}
}
else
{
x=lk[x]; split(,x);
if(!s[][x])
{
splay(x);
add(x,);
}
else
{
x=s[][x]; splay(x);
if(ch[x][]) add(ch[x][],);
v[x]++; update(x);
}
}
access(); splay();
if(v[]<=) printf("0\n");
else printf("1\n");
}
return ;
}
三叉神经树
由乃的OJ
起床困难综合症上树。这就是一道典型的树剖也可做，只是LCT少一个log的那种题（其实三叉神经树也是）。
起床困难综合症有两种做法，一种是按位贪心，对于每一位跑一遍所有门判断答案；另一种比较技巧，是把111..11,000...00放进去跑一遍，反正每一位是独立的，这样就得到了答案；显然，这道题多组询问，要是对于每一位跑一遍就太太太太太慢了，我们采用第二种方案。LCT上每个点维护111...11,000...00跑一遍后得到的结果，然后用一样的方法按位贪心就好啦！然而，换根的时候，链要进行反转，这些信息不就废了吗？所以，不仅要记录正着跑一遍的信息，也要记录反着跑一遍的信息。这个信息怎么合并呢？假设左儿子+$x$本身跑完后得到的结果是110001001，设为 $a$，那么对于11___1__1这几位，就要取右边全1得到的答案，对于__000_00_，就要取右边全0得到的答案，即$f(x)=(~a\&f_1(r)~)|(~(!a)\&f_0(r)~)$。这里要格外注意左右儿子的顺序问题，在update的时候，必须保证两个儿子的信息是对的。这很好处理，只要在update以前先pushdown两个儿子就好了。这题在luogu上比较容易通过，但是在bzoj上几乎是必TLE，据说树剖反而可以通过，但是我懒得再写一遍了(毕竟我是在练习LCT)，所以还是放一份LCT的代码吧。
# include <cstdio>
# include <iostream>
# define R register int
# define ULL unsigned long long
# define getchar() (S==T&&(T=(S=BB)+fread(BB,,<<,stdin),S==T)?EOF:*S++)
char BB[ << ], *S = BB, *T = BB; using namespace std; const int N=;
int n,m,k,x,y;
int opt[N],f[N],ch[N][],rev[N],sta[N];
ULL q,t,v[N],f1[N],f2[N],f3[N],f4[N]; void pushdown (int x)
{
if(!rev[x]) return ;
rev[x]=; swap(ch[x][],ch[x][]);
if(ch[x][]) rev[ ch[x][] ]^=;
if(ch[x][]) rev[ ch[x][] ]^=;
swap(f1[x],f3[x]); swap(f2[x],f4[x]);
} void update (int x)
{
if(ch[x][]) pushdown(ch[x][]);
if(ch[x][]) pushdown(ch[x][]);
int l=ch[x][],r=ch[x][];
if(opt[x]==)
{
f1[x]=f1[l]&v[x]; f1[x]=(f1[x]&f1[r])|((~f1[x])&f2[r]);
f2[x]=f2[l]&v[x]; f2[x]=(f2[x]&f1[r])|((~f2[x])&f2[r]);
f3[x]=f3[r]&v[x]; f3[x]=(f3[x]&f3[l])|((~f3[x])&f4[l]);
f4[x]=f4[r]&v[x]; f4[x]=(f4[x]&f3[l])|((~f4[x])&f4[l]);
}
else if(opt[x]==)
{
f1[x]=f1[l]|v[x]; f1[x]=(f1[x]&f1[r])|((~f1[x])&f2[r]);
f2[x]=f2[l]|v[x]; f2[x]=(f2[x]&f1[r])|((~f2[x])&f2[r]);
f3[x]=f3[r]|v[x]; f3[x]=(f3[x]&f3[l])|((~f3[x])&f4[l]);
f4[x]=f4[r]|v[x]; f4[x]=(f4[x]&f3[l])|((~f4[x])&f4[l]);
}
else
{
f1[x]=f1[l]^v[x]; f1[x]=(f1[x]&f1[r])|((~f1[x])&f2[r]);
f2[x]=f2[l]^v[x]; f2[x]=(f2[x]&f1[r])|((~f2[x])&f2[r]);
f3[x]=f3[r]^v[x]; f3[x]=(f3[x]&f3[l])|((~f3[x])&f4[l]);
f4[x]=f4[r]^v[x]; f4[x]=(f4[x]&f3[l])|((~f4[x])&f4[l]);
}
} inline bool isntroot (int x) { return (ch[ f[x] ][]==x||ch[ f[x] ][]==x); } inline int D (int x) { return ch[ f[x] ][]==x; } inline void rotate (int x)
{
int F=f[x],g=f[F];
int dx=D(x),df=D(F);
int k=ch[x][dx^];
ch[F][dx]=k; ch[x][dx^]=F;
if(ch[g][df]==F) ch[g][df]=x;
if(k) f[k]=F; f[F]=x; f[x]=g;
update(F); update(x);
} inline void splay (int x)
{
int y=x,tp=; sta[++tp]=x;
while(isntroot(y)) sta[++tp]=f[y],y=f[y];
for (R i=tp;i>=;--i) pushdown(sta[i]);
while(isntroot(x))
{
int t=f[x];
if(!isntroot(t)) rotate(x);
else if(D(t)==D(x)) rotate(t),rotate(x);
else rotate(x),rotate(x);
}
} inline ULL solve (int x,ULL v)
{
ULL ans=,s=;
for (R i=k-;i>=;--i)
{
ULL ans1=(1ull<<i)&f1[x],ans2=(1ull<<i)&f2[x];
if(s+(1ull<<i)>v) { ans+=ans2; continue; }
if(ans1>ans2) ans+=ans1,s+=(1ull<<i);
else ans+=ans2;
}
return ans;
} void access (int x)
{
int y=;
while()
{
splay(x); ch[x][]=y;
update(x);
y=x; x=f[x];
if(!x) return;
}
} void makeroot (int x) { access(x); splay(x); rev[x]^=; } void split (int x,int y) { makeroot(x); access(y); splay(x); } void link (int x,int y) { makeroot(x); f[x]=y; } int read1()
{
int x=;
char c=getchar();
while (!isdigit(c)) c=getchar();
while (isdigit(c)) x=(x<<)+(x<<)+(c^),c=getchar();
return x;
} ULL read2()
{
ULL x=;
char c=getchar();
while (!isdigit(c)) c=getchar();
while (isdigit(c)) x=(x<<)+(x<<)+(c^),c=getchar();
return x;
} int firs[N],h,dep[N];
struct edge { int too,nex; }g[N<<]; void add (int x,int y)
{
g[++h].nex=firs[x];
firs[x]=h;
g[h].too=y;
} void dfs (int x)
{
int j;
for (R i=firs[x];i;i=g[i].nex)
{
j=g[i].too;
if(dep[j]) continue;
dep[j]=; f[j]=x;
dfs(j);
}
} int main()
{
n=read1(); m=read1(); k=read1();
for (R i=;i<=n;++i)
opt[i]=read1(),v[i]=read2();
for (R i=;i<k;++i) q+=(1ull<<i);
f1[]=q; f3[]=q;
for (R i=;i<=n;++i)
{
if(opt[i]==) f1[i]=q&v[i],f2[i]=,f3[i]=q&v[i],f4[i]=;
else if(opt[i]==) f1[i]=q,f2[i]=v[i],f3[i]=q,f4[i]=v[i];
else f1[i]=q^v[i],f2[i]=v[i],f3[i]=q^v[i],f4[i]=v[i];
}
for (R i=;i<=n;++i)
{
x=read1(); y=read1();
add(x,y); add(y,x);
}
dep[]=; dfs();
for (R i=;i<=m;++i)
{
int o;
o=read1(); x=read1(); y=read1(); t=read2();
if(o==)
{
split(x,y);
printf("%llu\n",solve(x,t));
}
else
{
access(x); splay(x);
opt[x]=y; v[x]=t;
update(x);
}
}
return ;
}
由乃的OJ
维护生成树的LCT
大多数维护生成树的题首先都是以维护边权为基础的。LCT还可以维护边权嘛？化边为点就好啦。要么支持加边，要么支持删边（时间倒流），总之不能两者都支持，因为删边时可能会引起一系列以前加边时删掉的边重新被选中，那就根本没法做了。
魔法森林
题意概述：一张无向图中，每条边有两个属性$(a,b)$，要求找到一条 $1$ 到 $n$ 的路径，使得 $max(a)+max(b)$ 最小；$n<=50000,m<=100000$；
看上去有点难？两个参数互相影响，怎么处理才好呢？对于这种题目，我们常常采用固定一维信息的方法；
考虑枚举 $max(a)$，将 $\leq max(a)$ 的边加进去，求一个关于 $b$ 的最小生成树，就可以得到答案了。这样的复杂度是 $m^2\log m$ 的，过于不科学；
显然，随着枚举的那个 $max(a)$ 的增加，能用来构建最小生成树的边是越来越多的，也就是说...只有加边，没有删边？明示LCT维护关于b的最小生成树，这道题就做完了；
一点小细节：LCT的点数应为n+m，真·点的点权设为-inf，以防止被错误的当成路径最大值删掉。
# include <cstdio>
# include <iostream>
# include <algorithm>
# define R register int using namespace std; const int M=;
const int inf=;
int n,m,f[M],ch[M][],rev[M],v[M],id[M],sta[M],s[M];
struct edge { int x,y,a,b; }e[M]; bool cmp (edge a,edge b) { return a.a<b.a; } void update (int x)
{
v[x]=s[x]; id[x]=x;
if(v[ ch[x][] ]>v[x]) v[x]=v[ ch[x][] ],id[x]=id[ ch[x][] ];
if(v[ ch[x][] ]>v[x]) v[x]=v[ ch[x][] ],id[x]=id[ ch[x][] ];
} bool isntroot (int x) { return (ch[ f[x] ][]==x||ch[ f[x] ][]==x); } int D (int x) { return (ch[ f[x] ][]==x); } void rotate (int x)
{
int F=f[x],g=f[F];
int dx=D(x),df=D(F);
int k=ch[x][dx^];
ch[F][dx]=k; ch[x][dx^]=F;
if(ch[g][df]==F) ch[g][df]=x;
if(k) f[k]=F; f[F]=x; f[x]=g;
update(F); update(x);
} void pushdown (int x)
{
if(!rev[x]) return;
rev[x]=; swap(ch[x][],ch[x][]);
if(ch[x][]) rev[ ch[x][] ]^=;
if(ch[x][]) rev[ ch[x][] ]^=;
} void splay (int x)
{
int y=x,tp=; sta[++tp]=x;
while(isntroot(y)) sta[++tp]=f[y],y=f[y];
for (R i=tp;i>=;--i) pushdown(sta[i]);
while(isntroot(x))
{
int t=f[x];
if(!isntroot(t)) rotate(x);
else if(D(t)==D(x)) rotate(t),rotate(x);
else rotate(x),rotate(x);
}
} void access (int x)
{
int y=;
while()
{
splay(x); ch[x][]=y;
update(x);
y=x; x=f[x];
if(!x) return;
}
} void makeroot (int x)
{
access(x); splay(x);
rev[x]^=;
} void split (int x,int y) { makeroot(x); access(y); splay(y); } void link (int x,int y) { makeroot(x); f[x]=y; } void cut (int x,int y)
{
split(x,y);
ch[y][]=f[x]=;
update(y);
} int findroot (int x)
{
access(x); splay(x); pushdown(x);
while(ch[x][]) x=ch[x][],pushdown(x);
splay(x);
return x;
} int main()
{
scanf("%d%d",&n,&m);
for (R i=;i<=m;++i)
scanf("%d%d%d%d",&e[i].x,&e[i].y,&e[i].a,&e[i].b);
sort(e+,e++m,cmp);
int ans=inf;
for (R i=;i<=n;++i) v[i]=-inf,id[i]=i,s[i]=-inf;
for (R i=;i<=m;++i) v[i+n]=e[i].b,id[i+n]=i+n,s[i+n]=e[i].b;
for (R i=;i<=m;++i)
{
int x=e[i].x,y=e[i].y;
if(findroot(x)==findroot(y))
{
split(x,y);
if(v[y]>e[i].b)
{
int t=id[y];
cut(t,e[ t-n ].x),cut(t,e[ t-n ].y),link(x,i+n),link(i+n,y);
}
}else link(x,i+n),link(i+n,y);
if(findroot()==findroot(n))
{
split(,n);
ans=min(ans,e[i].a+v[n]);
}
}
if(ans==inf) printf("-1");
else printf("%d",ans);
return ;
}
魔法森林
水管局长
这道题就是删边啦，把它倒过来，转变为加边就好了；这里有一个小细节（指bzoj加强版）：整个过程中删去的边并不多，所以最后留下的边很多，用LCT来处理这部分很容易就TLE了。那怎么办呢？Kruscal求最小生成树，求完后再用LCT把它建出来就好啦！虽然LCT的理论复杂度是 $n\log n$，但实际上1e6跑起来就很费劲了，所以，还是多想想有没有哪些部分是可以优化的吧。
# include <cstdio>
# include <iostream>
# include <map>
# include <algorithm>
# define R register int
# define getchar() (S==T&&(T=(S=BB)+fread(BB,,<<,stdin),S==T)?EOF:*S++)
char BB[ << ], *S = BB, *T = BB; using namespace std; const int N=;
const int Q=;
const int inf=;
int n,m,q,x[N],y[N],t[N],vis[N],opt[Q],a[Q],b[Q];
int f[N],ch[N][],s[N],v[N],id[N],rev[N],sta[N];
int ans[Q];
map < pair<int,int>,int > M; void update (int x)
{
v[x]=s[x]; id[x]=x;
if(v[ ch[x][] ]>v[x]) v[x]=v[ ch[x][] ],id[x]=id[ ch[x][] ];
if(v[ ch[x][] ]>v[x]) v[x]=v[ ch[x][] ],id[x]=id[ ch[x][] ];
} bool isntroot (int x) { return (ch[ f[x] ][]==x||ch[ f[x] ][]==x); } int D (int x) { return (ch[ f[x] ][]==x); } void rotate (int x)
{
int F=f[x],g=f[F];
int dx=D(x),df=D(F);
int k=ch[x][dx^];
ch[F][dx]=k; ch[x][dx^]=F;
if(ch[g][df]==F) ch[g][df]=x;
if(k) f[k]=F; f[F]=x; f[x]=g;
update(F); update(x);
} void pushdown (int x)
{
if(!rev[x]) return;
rev[x]=; swap(ch[x][],ch[x][]);
if(ch[x][]) rev[ ch[x][] ]^=;
if(ch[x][]) rev[ ch[x][] ]^=;
} void splay (int x)
{
int y=x,tp=; sta[++tp]=x;
while(isntroot(y)) sta[++tp]=f[y],y=f[y];
for (R i=tp;i>=;--i) pushdown(sta[i]);
while(isntroot(x))
{
int t=f[x];
if(!isntroot(t)) rotate(x);
else if(D(t)==D(x)) rotate(t),rotate(x);
else rotate(x),rotate(x);
}
} void access (int x)
{
int y=;
while()
{
splay(x); ch[x][]=y;
update(x);
y=x; x=f[x];
if(!x) return;
}
} void makeroot (int x)
{
access(x); splay(x);
rev[x]^=;
} void split (int x,int y) { makeroot(x); access(y); splay(y); } void link (int x,int y) { makeroot(x); f[x]=y; } void cut (int x,int y)
{
split(x,y);
ch[y][]=f[x]=;
update(y);
} int findroot (int x)
{
access(x); splay(x); pushdown(x);
while(ch[x][]) x=ch[x][],pushdown(x);
splay(x);
return x;
} void ins (int i)
{
split(x[i],y[i]);
if(v[ y[i] ]<=t[i]) return;
int pos=id[ y[i] ];
cut(pos,x[pos-n]); cut(pos,y[pos-n]);
link(i+n,x[i]); link(i+n,y[i]);
} int read()
{
int x=;
char c=getchar();
while (!isdigit(c)) c=getchar();
while (isdigit(c)) x=(x<<)+(x<<)+(c^),c=getchar();
return x;
} struct edge { int x,y,z,id; }e[N];
int tf[N],eh; int fa (int x)
{
if(tf[x]==x) return x;
return tf[x]=fa(tf[x]);
} bool cmp (edge a,edge b) { return a.z<b.z; } void kruscal()
{
for (R i=;i<=n+m;++i) tf[i]=i;
sort(e+,e++eh,cmp);
for (R i=;i<=eh;++i)
{
int x=e[i].x,y=e[i].y;
x=fa(x); y=fa(y);
if(x==y) continue;
tf[x]=y;
link(e[i].id+n,e[i].x);
link(e[i].id+n,e[i].y);
}
} int main()
{
n=read(),m=read(),q=read();
v[]=s[]=-inf;
for (R i=;i<=n;++i)
v[i]=-inf,s[i]=-inf,id[i]=i;
for (R i=;i<=m;++i)
{
x[i]=read(); y[i]=read(); t[i]=read();
v[i+n]=t[i]; s[i+n]=t[i]; id[i+n]=i+n;
if(x[i]>y[i]) swap(x[i],y[i]);
M[ make_pair(x[i],y[i]) ]=i;
}
for (R i=;i<=q;++i)
{
opt[i]=read(); a[i]=read(); b[i]=read();
if(a[i]>b[i]) swap(a[i],b[i]);
if(opt[i]==) continue;
vis[ M[ make_pair(a[i],b[i]) ] ]=;
}
for (R i=;i<=m;++i)
if(!vis[i])
{
eh++;
e[eh].x=x[i]; e[eh].y=y[i]; e[eh].z=t[i];
e[eh].id=i;
}
kruscal();
for (R i=q;i>=;--i)
{
if(opt[i]==)
{
split(a[i],b[i]);
ans[i]=v[ b[i] ];
}
else
ins(M[ make_pair(a[i],b[i]) ]);
}
for (R i=;i<=q;++i)
if(opt[i]==) printf("%d\n",ans[i]);
return ;
}
水管局长
最小差值生成树
好了好了，我知道我很水，几乎一样的题做三遍，但是这回我是用虚拟机里的emacs写的这道题，所以也有一定意义啦~
没什么好说的，枚举最大值，成环的时候删最小值就好了。
一点小细节：如何求当前LCT中最小边的编号？开一个桶，记录每条边是否存在，因为随着边的增加，最小边的编号单调不减，可以用一个指针维护；
# include <cstdio>
# include <iostream>
# include <algorithm>
# define R register int using namespace std; const int N=;
const int inf=;
int n,m,it[N],ed;
int f[N],ch[N][],v[N],s[N],id[N],rev[N],tf[N];
int sta[N];
struct edge { int x,y,z; }e[N]; bool isntroot (int x) { return (ch[ f[x] ][]==x||ch[ f[x] ][]==x); } int D (int x) { return ch[ f[x] ][]==x; } void update (int x)
{
id[x]=x; s[x]=v[x];
if(s[ ch[x][] ]<s[x])
s[x]=s[ ch[x][] ],id[x]=id[ ch[x][] ];
if(s[ ch[x][] ]<s[x])
s[x]=s[ ch[x][] ],id[x]=id[ ch[x][] ];
} void pushdown (int x)
{
if(!rev[x]) return; rev[x]=;
if(ch[x][]) rev[ ch[x][] ]^=;
if(ch[x][]) rev[ ch[x][] ]^=;
swap(ch[x][],ch[x][]);
} void rotate (int x)
{
int F=f[x],g=f[F];
int dx=D(x),df=D(F);
int k=ch[x][dx^];
ch[x][dx^]=F; ch[F][dx]=k;
if(ch[g][df]==F) ch[g][df]=x;
if(k) f[k]=F; f[F]=x; f[x]=g;
update(F); update(x);
} void splay (int x)
{
int y=x,tp=; sta[++tp]=x;
while(isntroot(y)) sta[++tp]=f[y],y=f[y];
for (R i=tp;i>=;--i) pushdown(sta[i]);
while(isntroot(x))
{
int t=f[x];
if(!isntroot(t)) rotate(x);
else if(D(x)==D(t)) rotate(t),rotate(x);
else rotate(x),rotate(x);
}
} void access (int x)
{
int y=;
while()
{
splay(x); ch[x][]=y;
update(x);
y=x; x=f[x];
if(!x) return;
}
} void makeroot (int x)
{
access(x); splay(x);
rev[x]^=;
} void split (int x,int y)
{
makeroot(x); access(y); splay(y);
} void link (int x,int y)
{
makeroot(x); f[x]=y;
} void cut (int x,int y)
{
split(x,y);
ch[y][]=f[x]=;
update(y);
} bool cmp (edge a,edge b) { return a.z<b.z; } int fa (int x)
{
if(x==tf[x]) return x;
return tf[x]=fa(tf[x]);
} int main()
{
scanf("%d%d",&n,&m);
v[]=s[]=inf;
for (R i=;i<=n;++i)
v[i]=inf,id[i]=i,s[i]=inf;
for (R i=;i<=m;++i)
scanf("%d%d%d",&e[i].x,&e[i].y,&e[i].z);
sort(e+,e++m,cmp);
for (R i=;i<=m;++i) v[i+n]=s[i+n]=e[i].z,id[i+n]=i+n;
int mp=n+,ans=inf;
for (R i=;i<=n;++i) tf[i]=i;
for (R i=;i<=m;++i)
{
int x=e[i].x,y=e[i].y;
if(x==y) continue;
if(fa(x)==fa(y))
{
split(x,y);
int pos=id[y]; it[pos]=;
cut(pos,e[pos-n].x); cut(pos,e[pos-n].y);
link(i+n,x); link(i+n,y);
it[i+n]=;
}
else link(i+n,x),link(i+n,y),it[i+n]=,ed++,tf[ fa(x) ]=fa(y);
while(it[mp]==) mp++;
if(ed==n-) ans=min(ans,e[i].z-e[mp-n].z);
}
printf("%d",ans);
return ;
}
最小差值生成树
维护子树信息的LCT
LCT更擅长做一些关于树链的问题，但是呢...毒瘤出题人总能想办法将数据结构的功能扩展再扩展，所以就有了维护子树信息的LCT。
其实，LCT维护子树听起来奥妙重重，写起来却没多难；首先，子树=实子树+虚子树；是否可以考虑对于每个点维护它的虚子树信息呢？其实是可以哒。下面将以维护子树大小为例讲讲这种LCT，$si[x]$ 表示的是x所有虚子树的大小的和；
首先是update：
access:
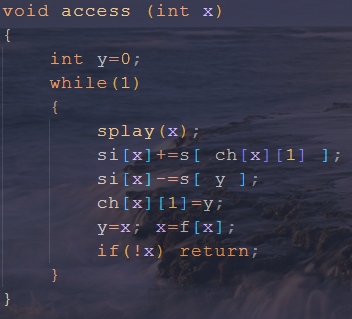
link:
然后就没了...因为子树信息只有在新加儿子或者切换虚实儿子的时候才会有影响，在别的时候根本不用改动；
大融合
掌握了LCT维护子树信息的方法，这道题就很简单啦。
首先我们都知道，这个边的“负载”指的就是(n-x到y方向的子树大小)*(n-y到x方向的子树大小)；不过这样有一点点麻烦，可以考虑转化，先 $split(x,y)$，然后答案就是(y的虚子树和+1)*(x的虚子树和+1)啦；画个图方便理解：
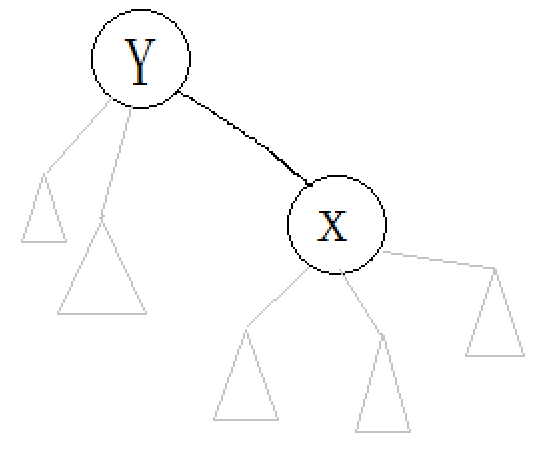
# include <cstdio>
# include <iostream>
# include <cstring>
# define ll long long
# define R register int using namespace std; const int N=;
int n,q,x,y;
int f[N],ch[N][],s[N],si[N],rev[N],sta[N];
char st[]; bool isntroot (int x)
{
return (ch[ f[x] ][]==x||ch[ f[x] ][]==x);
} void pushdown (int x)
{
if(!rev[x]) return; rev[x]=;
if(ch[x][]) rev[ ch[x][] ]^=;
if(ch[x][]) rev[ ch[x][] ]^=;
swap(ch[x][],ch[x][]);
} int D (int x)
{
return ch[ f[x] ][]==x;
} void update (int x)
{
s[x]=si[x]+s[ ch[x][] ]+s[ ch[x][] ]+;
} void rotate (int x)
{
int F=f[x],g=f[F];
int dx=D(x),df=D(F);
int k=ch[x][dx^];
ch[x][dx^]=F; ch[F][dx]=k;
if(ch[g][df]==F) ch[g][df]=x;
if(k) f[k]=F; f[F]=x; f[x]=g;
update(F); update(x);
} void splay (int x)
{
int tp=,y=x; sta[++tp]=x;
while(isntroot(y)) sta[++tp]=f[y],y=f[y];
for (R i=tp;i>=;--i) pushdown(sta[i]);
while(isntroot(x))
{
int t=f[x];
if(!isntroot(t)) rotate(x);
else if(D(t)==D(x)) rotate(t),rotate(x);
else rotate(x),rotate(x);
}
} void access (int x)
{
int y=;
while()
{
splay(x);
si[x]+=s[ ch[x][] ];
si[x]-=s[ y ];
ch[x][]=y;
y=x; x=f[x];
if(!x) return;
}
} void makeroot (int x)
{
access(x); splay(x);
rev[x]^=;
} void link (int x,int y)
{
makeroot(x); access(y); splay(y);
f[x]=y; si[y]+=s[x]; s[y]+=s[x];
} ll ask (int x,int y)
{
makeroot(x); access(y); splay(y);
return 1LL*(si[y]+)*s[x];
} int main()
{
scanf("%d%d",&n,&q);
for (R i=;i<=n;++i) s[i]=;
for (R i=;i<=q;++i)
{
scanf("%s",st+);
scanf("%d%d",&x,&y);
if(st[]=='A')
link(x,y);
else
printf("%lld\n",ask(x,y));
}
return ;
}
大融合
首都
一道很神神神神神神的题！
题意概述：维护一个森林，要求支持动态加边，问某个点目前所在联通块的重心，
具有技巧性的LCT
树点涂色
LCT做题笔记的更多相关文章
- C语言程序设计做题笔记之C语言基础知识(下)
C 语言是一种功能强大.简洁的计算机语言,通过它可以编写程序,指挥计算机完成指定的任务.我们可以利用C语言创建程序(即一组指令),并让计算机依指令行 事.并且C是相当灵活的,用于执行计算机程序能完成的 ...
- C语言程序设计做题笔记之C语言基础知识（上）
C语言是一种功能强大.简洁的计算机语言,通过它可以编写程序,指挥计算机完成指定的任务.我们可以利用C语言创建程序(即一组指令),并让计算机依指令行事.并且C是相当灵活的,用于执行计算机程序能完成的几乎 ...
- SDOI2017 R1做题笔记
SDOI2017 R1做题笔记 梦想还是要有的,万一哪天就做完了呢? 也就是说现在还没做完. 哈哈哈我竟然做完了-2019.3.29 20:30
- SDOI2014 R1做题笔记
SDOI2014 R1做题笔记 经过很久很久的时间,shzr又做完了SDOI2014一轮的题目. 但是我不想写做题笔记(
- SDOI2016 R1做题笔记
SDOI2016 R1做题笔记 经过很久很久的时间,shzr终于做完了SDOI2016一轮的题目. 其实没想到竟然是2016年的题目先做完,因为14年的六个题很早就做了四个了,但是后两个有点开不动.. ...
- java做题笔记
java做题笔记 1. 初始化过程是这样的: 1.首先,初始化父类中的静态成员变量和静态代码块,按照在程序中出现的顺序初始化: 2.然后,初始化子类中的静态成员变量和静态代码块,按照在程序中出现的顺序 ...
- SAM 做题笔记（各种技巧，持续更新，SA）
SAM 感性瞎扯. 这里是 SAM 做题笔记. 本来是在一篇随笔里面,然后 Latex 太多加载不过来就分成了两篇. 标 * 的是推荐一做的题目. trick 是我总结的技巧. I. P3804 [模 ...
- PKUWC/SC 做题笔记
去年不知道干了些啥,什么省选/营题都没做. 现在赶应该还来得及(?) 「PKUWC2018」Minimax Done 2019.12.04 9:38:55 线段树合并船新玩法??? \(O(n^2)\ ...
- POI做题笔记
POI2011 Conspiracy (2-SAT) Description \(n\leq 5000\) Solution 发现可拆点然后使用2-SAT做,由于特殊的关系,可以证明每次只能交换两个集 ...
随机推荐
- MySQL_(Java)使用preparestatement解决SQL注入的问题
MySQL_(Java)使用JDBC向数据库发起查询请求 传送门 MySQL_(Java)使用JDBC创建用户名和密码校验查询方法 传送门 MySQL数据库中的数据,数据库名garysql,表名gar ...
- 系统芯片 SoC
SoC的定义多种多样,由于其内涵丰富.应用范围广,很难给出准确定义.一般说来, SoC称为系统级芯片,也有称片上系统,意指它是一个产品,是一个有专用目标的集成电路,其中包含完整系统并有嵌入软件的全部内 ...
- DB 分库分表（4）：多数据源的事务处理
系统经sharding改造之后,原来单一的数据库会演变成多个数据库,如何确保多数据源同时操作的原子性和一致性是不得不考虑的一个问题.总体上看,目前对于一个分布式系统的事务处理有三种方式:分布式事务.基 ...
- Angular5.0之 安装指定版本Angular CLI
我们可能会发现按照网上的方式下载安装后,使用Angular CLI生成的项目并不是我们想要的Angular的版本,因为在我们没有指定安装版本的前提下,默认会下载最新的版本安装,然而不同的Angular ...
- Oracle 11g的日志路径
Oracle数据库的最常用问题定位日志是alert日志,Oracle数据库的日志文件alert_$ORACLE_SID.log记录了重作日志的转换,数据库启动和关闭,数据库结构的改变,回退段的修改,死 ...
- If表达式 kotlin(8)
If表达式 在 Kotlin 中, if 是一个表达式,即它会返回一个值. 因此就不需要三元运算符(条件 ? 然 后 : 否则) ,因为普通的 if 就能胜任这个角色. // 传统用法 var max ...
- windows上配置pytorch
操作系统:win10 已安装程序:Python 3.6 + Anaconda 5.1.0 + CUDA 9 pytorch官网:https://pytorch.org/ 1.进入官网,从Get Sta ...
- 删除github上的一个repository
在学github之初,我们免不了会建立一些简单的repository,那么,如何删掉它们呢? 第一步,打开所要删除的repository,比如:meilin.github.io 第二步,点击setti ...
- When Database Sharding is Appropriate DATABASE SHARDING
w横切 http://www.agildata.com/database-sharding/ When Database Sharding is Appropriate Database Shardi ...
- CoordinatorLayout使用全解析
版权声明:本文为博主原创文章,未经博主允许不得转载. https://blog.csdn.net/u012124438/article/details/56701641 CoordinatorLayo ...