P2822 组合数问题——巧用前缀和

P2822 组合数问题

求的是C（i,j）有多少个是k的倍数；

首先，求组合数是有技巧的，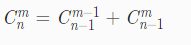

用杨辉三角求组合数，爽的一批；

但是，这样只能得90分，两个点T了；

因为k是不变的，我们可以用前缀和的思想求出每个点的答案；

注意ans[i][i+1]=ans[i][i];因为下一个点是比上一个点多一个的；

为了不超过整数范围，我们可以%k；

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int maxn=;
int c[maxn][maxn];
int n,k;
int ans[maxn][maxn];
void build()
{
    c[][]=;
    c[][]=c[][]=;
    for(int i=;i<=;i++)
    {
        c[i][]=;
        for(int j=;j<=i;j++)
        {
            c[i][j]=c[i-][j]%k+c[i-][j-]%k;
            ans[i][j]=ans[i-][j]+ans[i][j-]-ans[i-][j-];
            if(c[i][j]%k==) ans[i][j]++;
        }
        ans[i][i+]=ans[i][i];
    }
}
int T,m;
int x;
int main()
{
 
    scanf("%d%d",&T,&k);
    build();
    while(T--)
    {
        scanf("%d%d",&n,&m);
        x=min(n,m);
        printf("%d\n",ans[n][x]);
    }
    return ;
}