【java多线程】队列系统之PriorityBlockingQueue源码

一、二叉堆

如题，二叉堆是一种基础数据结构

事实上支持的操作也是挺有限的（相对于其他数据结构而言），也就插入，查询，删除这一类

对了这篇文章中讲到的堆都是二叉堆，而不是斜堆，左偏树，斐波那契堆什么的 我都不会啊

二叉堆的表现形式：我们可以使用数组的索引来表示元素在二叉堆中的位置。

从二叉堆中，我们可以得出：

· 元素k的父节点所在的位置为 ：k的位置/2]

· 元素k的子节点所在的位置为：2*k的位置和2*k的位置+1

跟据以上规则，我们可以使用二维数组的索引来表示二叉堆。通过二叉堆，我们可以实现插入和删除最大值都达到O(nlogn)的时间复杂度。

对于堆来说，最大元素已经位于根节点，那么删除操作就是移除并返回根节点元素，这时候二叉堆就需要重新排列；当插入新的元素的时候，也需要重新排列二叉堆以满足二叉堆的定义。现在就来看这两种操作。

实现优先级队列的思路及算法复杂度的考量

• 如果使用无序数组，那么每一次插入的时候，直接在数组末尾插入即可，时间复杂度为O(1)，但是如果要获取最大值，或者最小值返回的话，则需要进行查找，这时时间复杂度为O(n)。
• 如果使用有序数组，那么每一次插入的时候，通过插入排序将元素放到正确的位置，时间复杂度为O(n)，但是如果要获取最大值的话，由于元阿苏已经有序，直接返回数组末尾的 元素即可，所以时间复杂度为O(1).所以采用普通的数组或者链表实现，无法使得插入和排序都达到比较好的时间复杂度。所以我们需要采用新的数据结构来实现。下面就开始介绍如何采用二叉堆(binary heap)来实现优先级队列
• 跟据以上规则，我们可以使用二维数组的索引来表示二叉堆。通过二叉堆，我们可以实现插入和删除最大值都达到O(nlogn)的时间复杂度。

二、二叉堆

由于堆是一棵形态规则的二叉树，因此堆的父节点和孩子节点存在如下关系：

设父节点的编号为 i, 则其左孩子节点的编号为2*i+1, 右孩子节点的编号为2*i+2
设孩子节点的编号为i, 则其父节点的编号为(i-1)/2

什么是二叉堆？

二叉堆本质上是一种完全二叉树，它分为两个类型：

1.最大堆

2.最小堆

什么是最大堆呢？最大堆任何一个父节点的值，都大于等于它左右孩子节点的值。

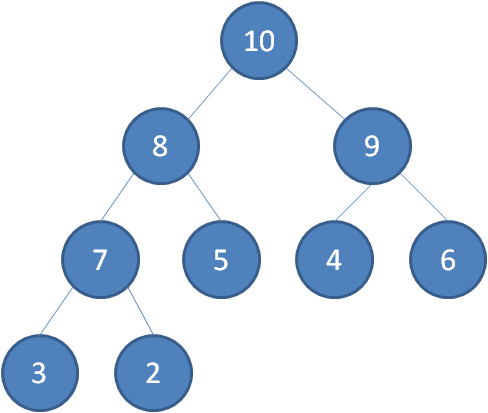
什么是最小堆呢？最小堆任何一个父节点的值，都小于等于它左右孩子节点的值。

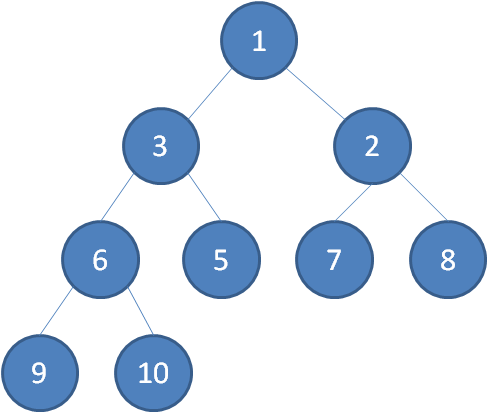
二叉堆的根节点叫做堆顶。

最大堆和最小堆的特点，决定了在最大堆的堆顶是整个堆中的最大元素；最小堆的堆顶是整个堆中的最小元素。

堆的自我调整

对于二叉堆，如下有几种操作：

插入节点

删除节点

构建二叉堆

这几种操作都是基于堆的自我调整。

下面让我们以最小堆为例，看一看二叉堆是如何进行自我调整的。

1.插入节点

二叉堆的节点插入，插入位置是完全二叉树的最后一个位置。比如我们插入一个新节点，值是 0。

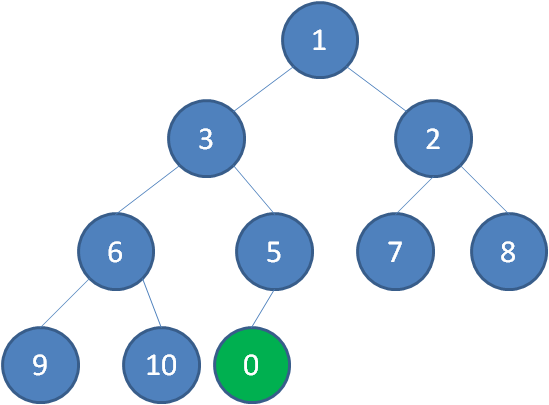
这时候，我们让节点0的它的父节点5做比较，如果0小于5，则让新节点“上浮”，和父节点交换位置。

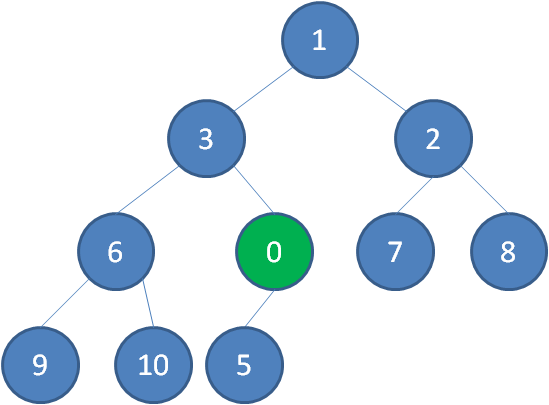
继续用节点0和父节点3做比较，如果0小于3，则让新节点继续“上浮”。

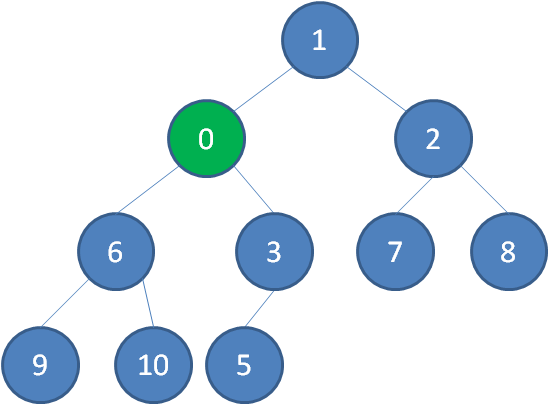
继续比较，最终让新节点0上浮到了堆顶位置。

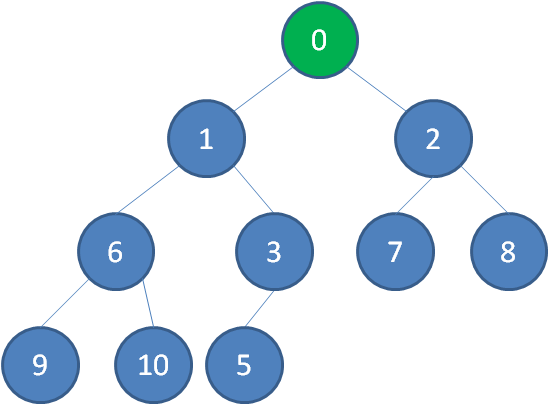
2.删除节点

二叉堆的节点删除过程和插入过程正好相反，所删除的是处于堆顶的节点。比如我们删除最小堆的堆顶节点1。

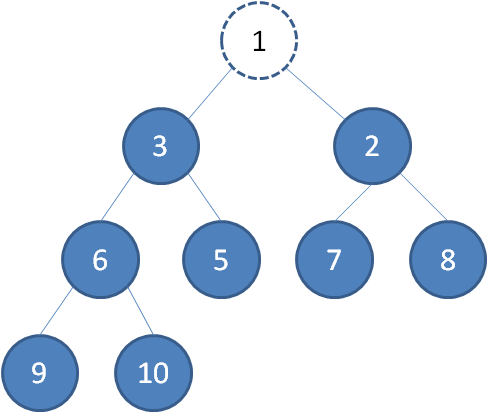
这时候，为了维持完全二叉树的结构，我们把堆的最后一个节点10补到原本堆顶的位置。

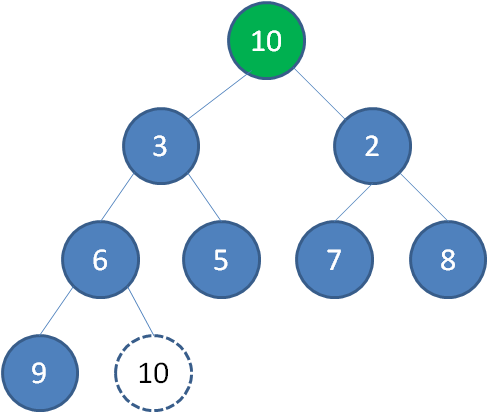
接下来我们让移动到堆顶的节点10和它的左右孩子进行比较，如果左右孩子中最小的一个（显然是节点2）比节点10小，那么让节点10“下沉”。

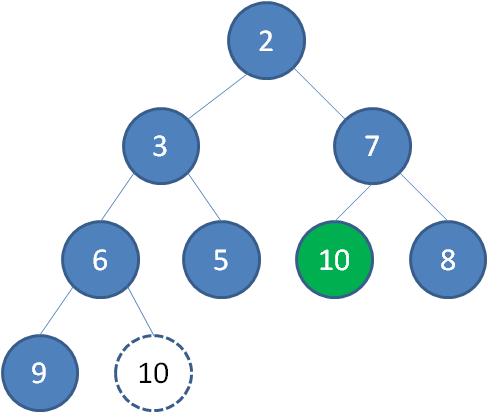
这样一来，二叉堆重新得到了调整。

3.构建二叉堆

构建二叉堆，也就是把一个无序的完全二叉树调整为二叉堆，本质上就是让所有非叶子节点依次下沉。

我们举一个无序完全二叉树的例子：

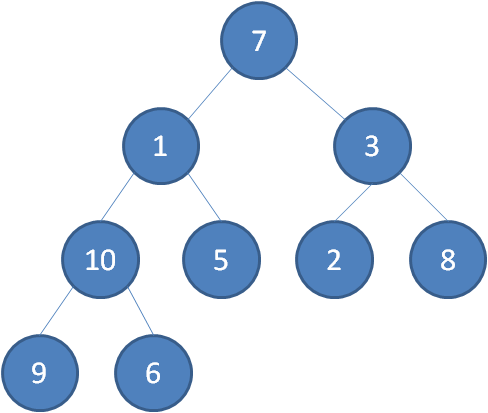
首先，我们从最后一个非叶子节点开始，也就是从节点10开始。如果节点10大于它左右孩子中最小的一个，则节点10下沉。

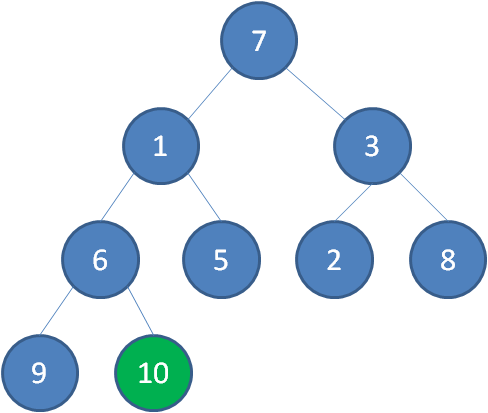
接下来轮到节点3，如果节点3大于它左右孩子中最小的一个，则节点3下沉。

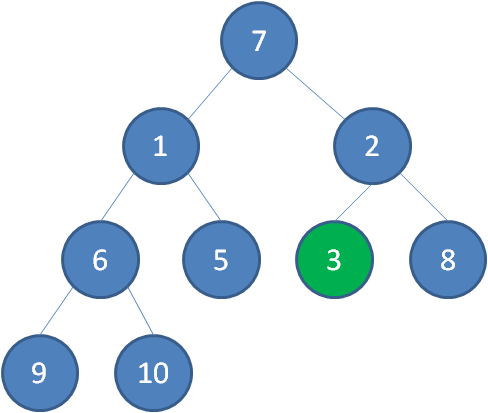
接下来轮到节点1，如果节点1大于它左右孩子中最小的一个，则节点1下沉。事实上节点1小于它的左右孩子，所以不用改变。

接下来轮到节点7，如果节点7大于它左右孩子中最小的一个，则节点7下沉。

节点7继续比较，继续下沉。

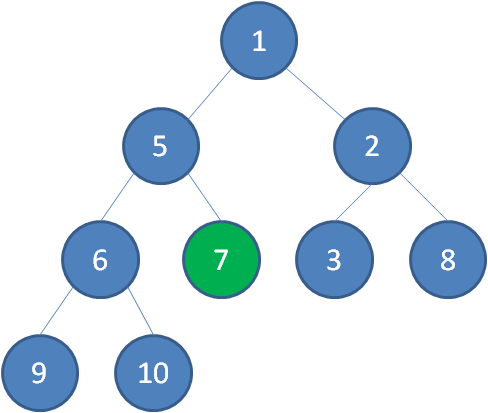
这样一来，一颗无序的完全二叉树就构建成了一个最小堆。

堆的代码实现

在撸代码之前，我们还需要明确一点：

二叉堆虽然是一颗完全二叉树，但它的存储方式并不是链式存储，而是顺序存储。换句话说，二叉堆的所有节点都存储在数组当中。

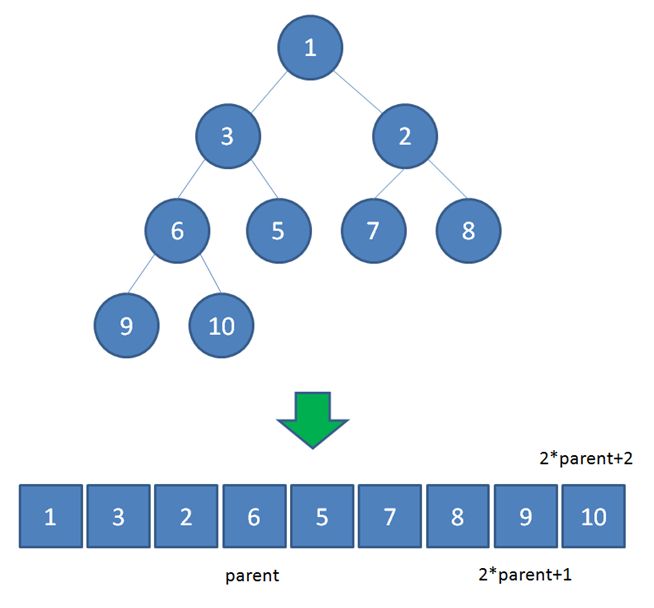
数组中，在没有左右指针的情况下，如何定位到一个父节点的左孩子和右孩子呢？

像图中那样，我们可以依靠数组下标来计算

假设父节点的下标是parent，那么它的左孩子下标就是 2*parent+1；它的右孩子下标就是  2*parent+2 。

比如上面例子中，节点6包含9和10两个孩子，节点6在数组中的下标是3，节点9在数组中的下标是7，节点10在数组中的下标是8。

7 = 3*2+1

8 = 3*2+2

刚好符合规律。

有了这个前提，下面的代码就更好理解了：

参考：

https://www.cnblogs.com/yangecnu/p/Introduce-Priority-Queue-And-Heap-Sort.html

https://www.cnblogs.com/henry-1202/p/9307927.html

http://www.ijiandao.com/2b/baijia/168869.html

http://blog.jobbole.com/113552/