luogu1856

P1856 [USACO5.5]矩形周长Picture

题目背景

墙上贴着许多形状相同的海报、照片。它们的边都是水平和垂直的。每个矩形图片可能部分或全部的覆盖了其他图片。所有矩形合并后的边长称为周长。

题目描述

编写一个程序计算周长。

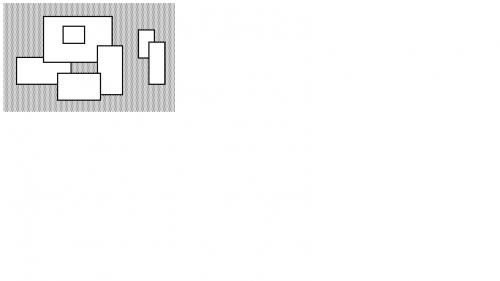
如图1所示7个矩形。

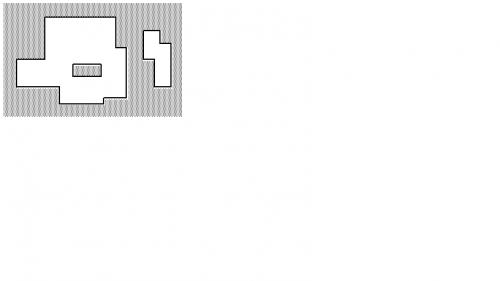
如图2所示，所有矩形的边界。所有矩形顶点的坐标都是整数。

输入输出格式

输入格式：

输入文件的第一行是一个整数N（0<=N<5000），表示有多少个矩形。接下来N行给出了每一个矩形左下角坐标和右上角坐标（所有坐标的数值范围都在-10000到10000之间）。

输出格式：

输出文件只有一个正整数，表示所有矩形的周长。

输入输出样例

输入样例#1：

7
-15 0 5 10
-5 8 20 25
15 -4 24 14
0 -6 16 4
2 15 10 22
30 10 36 20
34 0 40 16

输出样例#1：

228

求周长和，不用离散的方法

记录最小值和最小值出现的个数

#include <cstdio>
#include <algorithm>
using namespace std;
#define N 10005
int n,x1[N],y1[N],x2[N],y2[N];
struct node{int x1,x2,y,op;}line[N];
inline bool cmp(node a,node b){return a.y!=b.y?a.y<b.y:a.op>b.op;}
struct SegmentTree{int l,r,mi,sum,lazy;}Tree[N<<];
inline void pushup(int x)
{
    if(Tree[x<<].mi==Tree[x<<|].mi)Tree[x].sum=Tree[x<<].sum+Tree[x<<|].sum, Tree[x].mi=Tree[x<<].mi;
    else if(Tree[x<<].mi<Tree[x<<|].mi)Tree[x].sum=Tree[x<<].sum, Tree[x].mi=Tree[x<<].mi;
    else Tree[x].sum=Tree[x<<|].sum, Tree[x].mi=Tree[x<<|].mi;
}
inline void ADD(int x,int v){Tree[x].lazy+=v;Tree[x].mi+=v;}
inline void pushdown(int x){ADD(x<<,Tree[x].lazy); ADD(x<<|,Tree[x].lazy); Tree[x].lazy=;}
inline void build(int l,int r,int x)
{
    Tree[x].l=l; Tree[x].r=r; Tree[x].lazy=;
    if(l==r){Tree[x].sum=;Tree[x].mi=;return;}
    int mid=(l+r)>>;build(l,mid,x<<);build(mid+,r,x<<|);pushup(x);
}
inline void updata(int l,int r,int x,int v)
{
    if(l==Tree[x].l&&Tree[x].r==r){Tree[x].lazy+=v;Tree[x].mi+=v;return;}
    if(Tree[x].lazy!=) pushdown(x); int mid=(Tree[x].l+Tree[x].r)>>;
    if(r<=mid)updata(l,r,x<<,v); else if(l>mid) updata(l,r,x<<|,v);
    else updata(l,mid,x<<,v), updata(mid+,r,x<<|,v); pushup(x);
}
int main()
{
    int i,ans=; scanf("%d",&n);
    for(i=;i<=n;i++)
    {
        scanf("%d%d%d%d",&x1[i],&y1[i],&x2[i],&y2[i]);
        line[i*-].x1=line[i*].x1=x1[i]; line[i*-].x2=line[i*].x2=x2[i]-;
        line[i*-].y=y1[i]; line[i*].y=y2[i]; line[i*-].op=; line[i*].op=-;
    }n*=;
    sort(line+,line+n+,cmp); build(-N,N,);
    for(i=;i<=n;i++)
    {
        int oo=Tree[].sum*(Tree[].mi==); updata(line[i].x1,line[i].x2,,line[i].op); ans+=abs(oo-Tree[].sum*(Tree[].mi==));
    }
    for(i=;i<=n;i++)
    {
        line[i*-].x1=line[i*].x1=y1[i]; line[i*-].x2=line[i*].x2=y2[i]-;
        line[i*-].y=x1[i]; line[i*].y=x2[i]; line[i*-].op=; line[i*].op=-;
    }
    sort(line+,line+n+,cmp); build(-N,N,);
    for(i=;i<=n;i++)
    {
        int oo=Tree[].sum*(Tree[].mi==); updata(line[i].x1,line[i].x2,,line[i].op); ans+=abs(oo-Tree[].sum*(Tree[].mi==));
    }
    printf("%d\n",ans);
}