cordic
cordic里向量旋转得到新向量,利用的是旋转矩阵
摘自百度百科维基百科
旋转矩阵(Rotation matrix)是在乘以一个向量的时候改变向量的方向但不改变大小的效果的矩阵。旋转矩阵不包括反演,它不可以把右手坐标系改变成左手坐标系或反之。所有旋转加上反演形成了正交矩阵的集合。对于3D坐标系,任意两个坐标系却不能等价。实际上,存在两种完全不同的3D坐标系:左手坐标系和右手坐标系。如果同属于左手坐标系或者右手坐标系,则可以通过旋转来重合,否则不可以

参考文献:
基于CORDIC 改进算法的反正切函数
在FPGA 中的实现
刘小会1,许蕾2,刘海颖2,王惠南1
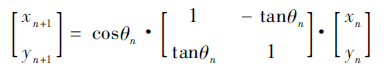
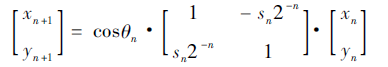

cordic的更多相关文章
- CORDIC原理与FPGA实现(2)
CORDIC算法实现极坐标(polar)到直角坐标系(Cartesian)的变换. 1: function [horizonal,vertical]=polar2car(mag, pha); 2: x ...
- CORDIC原理与FPGA实现(1)
CORDIC算法的来历与用途大家网上随处可以见到,这里写 一下自己的理解. 将P(x,y)旋转角度a得到新的坐标P’(x’,y’).这里的坐标变换为: x’= x cos(a) – y sin(a) ...
- 三角函数计算,Cordic 算法入门
[-] 三角函数计算Cordic 算法入门 从二分查找法说起 减少乘法运算 消除乘法运算 三角函数计算,Cordic 算法入门 三角函数的计算是个复杂的主题,有计算机之前,人们通常通过查找三角函数表来 ...
- (转)三角函数计算,Cordic 算法入门
由于最近要使用atan2函数,但是时间上消耗比较多,因而网上搜了一下简化的算法. 原帖地址:http://blog.csdn.net/liyuanbhu/article/details/8458769 ...
- 基于FPGA的cordic算法的verilog初步实现
最近在看cordic算法,由于还不会使用matlab,真是痛苦,一系列的笔算才大概明白了这个算法是怎么回事.于是尝试用verilog来实现.用verilog实现之前先参考软件的程序,于是先看了此博文h ...
- Cordic 算法之 反正切
在通信的算法中,常采用Cordic算法之一,知道角度产生正交的的正弦余弦, 或者知道正弦和余弦求角度,求反正切. 1. 求正弦和余弦值. 方法:旋转角度,得到正弦余弦值: 再旋转角度,到达下一个正弦余 ...
- Cordic 算法的原理介绍
cordic 算法知道正弦和余弦值,求反正切,即角度. 采用用不断的旋转求出对应的正弦余弦值,是一种近似求解发. 旋转的角度很讲求,每次旋转的角度必须使得 正切值近似等于 1/(2^N).旋转的目的是 ...
- Cordic算法——verilog实现
上两篇博文Cordic算法--圆周系统之旋转模式.Cordic算法--圆周系统之向量模式做了理论分析和实现,但是所用到的变量依然是浮点型,而cordic真正的用处是基于FPGA等只能处理定点的平台.只 ...
- Cordic算法——圆周系统之向量模式
旋转模式用来解决三角函数,实现极坐标到直角坐标的转换,基础理论请参考Cordic算法--圆周系统之旋转模式.那么,向量模式则用来解决反三角函数的问题,体现的应用主要是直角坐标向极坐标转换,即已知一点的 ...
- Cordic算法——圆周系统之旋转模式
三角函数的计算是个复杂的主题,有计算机之前,人们通常通过查找三角函数表来计算任意角度的三角函数的值.这种表格在人们刚刚产生三角函数的概念的时候就已经有了,它们通常是通过从已知值(比如sin(π/2)= ...
随机推荐
- PAT A1123 Is It a Complete AVL Tree (30 分)——AVL平衡二叉树,完全二叉树
An AVL tree is a self-balancing binary search tree. In an AVL tree, the heights of the two child sub ...
- 利用 ProtoThreads实现Arduino多线程处理(2)
转载请注明:@小五义http://www.cnblogs.com/xiaowuyiQQ群:64770604 感谢小V分享给大家的博文. 我在做产品设计的课题的时候,小五义推荐我使用Protothrea ...
- 学习CSS布局 - 没有布局
如果你只想把所有内容都塞进一栏里,那么不用设置任何布局也是OK的. 然而,如果用户把浏览器窗口调整的很大,这时阅读网页会非常难受: 读完每一行之后,你的视觉焦点要从右到左移动一大段距离. 试着调整下浏 ...
- (转)vim中多行注释
1.多行注释: 1. 首先按esc进入命令行模式下,按下Ctrl + v,进入列(也叫区块)模式; 2. 在行首使用上下键选择需要注释的多行; 3. 按下键盘(大写)“I”键,进入插入模式: ...
- 17-(基础入门篇)GPRS(Air202)串口
https://www.cnblogs.com/yangfengwu/p/9968716.html 现在看一下官方给的demo 其实只要有两个就好说了 module(...,package.seeal ...
- 二、java三大特性--继承
在讲解之前我们先看一个例子 Husband.java public class Husband { private String name; private String sex; privatein ...
- 使用Windows API进行串口编程
使用Windows API进行串口编程 串口通信一般分为四大步:打开串口->配置串口->读写串口->关闭串口,还可以在串口上监听读写等事件.1.打开和关闭串口Windows中串口 ...
- Luogu2612 ZJOI2012 波浪 DP
传送门 花掉了自己用来搞学科的时间做了这道题-- 一道类似的题:Here 考虑拆开绝对值计算贡献.那么我们对于\(1\)到\(N\)的排列,从小到大地将插入它们插入排列中. 假设我们现在计算到了数\( ...
- 生成线上用https证书,支持通配符和多域名,初学Let’s Encrypt用于IIS,纯本地手动
自简书发布的上篇<生成本地测试用https证书,支持通配符和多域名,初学OpenSSL>以来,本地测试用https用的妥妥的. 线上一直用的腾讯云的免费证书(每个域名都要一个证书(滑稽), ...
- dxteam团队项目终审报告
一. 团队成员的简介和个人博客地址 M1阶段 http://www.cnblogs.com/dxteam/p/3991514.html M2阶段 新成员 邓亚梅 http://www.cnblogs. ...
