BigDecimal常被忽略的问题

一：相除精度丢失的问题

　　BigDecimal的api除法相对加减乘要实现的复杂多了，只介绍常用的我遇到的问题：

　　问题：两数相除，如果9/3=3整除没问题，但是10/3=0.33333333......除不尽，这里不能让电脑一直除不尽，所以BigDecimal做出一些限制；

　　　必须按照（数，保留小数位（最好要合理限制最大精度），舍入方式）来操作

　

　　　否则就会抛出异常，例如：

 public static void main(String[] args) {

        BigDecimal a = new BigDecimal(10);
        BigDecimal b = new BigDecimal(3);
        BigDecimal c = a.divide(b);
    }

　　　执行：抛出

Exception in thread "main" java.lang.ArithmeticException: Non-terminating decimal expansion; no exact representable decimal result.
at java.math.BigDecimal.divide(BigDecimal.java:1616)

二：舍入方式精度丢失的问题

　　多数相乘时，请勿先进行四舍五入或者其他的方式，以最终计算结果为基础进行取舍精度，虽然一说就明白，但是这一个编码的习惯问题，特别是在金融行业。

　　舍入方式需要弄明白自己的业务才用，别为了用而随便选一个用

　　1.ROUND_UP：四舍五入模式从零四舍五入。

public static void main(String[] args) {

        BigDecimal a = new BigDecimal(0.31);
        BigDecimal b = new BigDecimal(3);
        BigDecimal c = a.divide(b,1,BigDecimal.ROUND_UP);
        LOGGER.error("原值：0.1033333...///"+c.toString()+"=0.2");

        //结论：0-9都是向前进一位（且当0后还有小数位为前提）

}

　　2.ROUND_DOWN 四舍五入模式到四舍五入接近零。

public static void main(String[] args) {
　　　　　
        BigDecimal a = new BigDecimal(0.39);
        BigDecimal b = new BigDecimal(1);
        BigDecimal c = a.divide(b,1,BigDecimal.ROUND_DOWN);
        LOGGER.error("原值：0.39///"+c.toString()+"=0.3");
　　　　　　//结论：1-9都是向前进一位
    }

　　3.ROUND_CEILING 四舍五入到正无穷。

public static void main(String[] args) {

        BigDecimal a = new BigDecimal(0.301);
        BigDecimal b = new BigDecimal(1);
        BigDecimal c = a.divide(b,1,BigDecimal.ROUND_CEILING);
        LOGGER.error("原值：0.301///"+c.toString()+"=0.4");
　　　　//结论：与第一种类似，区别就是舍入到正无穷的范围大，当值为负数时舍入失效，当用第四种解决
    }

　　4.ROUND_FLOOR 四舍五入到负无穷

public static void main(String[] args) {

        BigDecimal a = new BigDecimal(-0.301);
        BigDecimal b = new BigDecimal(1);
        BigDecimal c = a.divide(b,1,BigDecimal.ROUND_FLOOR);
        LOGGER.error("原值：0.301///"+c.toString()+"=0.4");
　　　　　//结论：与上面的正无穷舍入的方式相反，可以互补
    }

　　5.ROUND_HALF_UP 四舍五入方式四舍五入，除非两个邻边距离相等，则四舍五入。

public static void main(String[] args) {

        BigDecimal a = new BigDecimal(-0.36);
        BigDecimal b = new BigDecimal(1);
        BigDecimal c = a.divide(b,1,BigDecimal.ROUND_HALF_UP);
        LOGGER.error("原值：-0.36///"+c.toString()+"=-0.4");
        //结论：正负数相同，以5为分界，<=5舍掉，>5的进1
    }

　　6.ROUND_HALF_DOWN 四舍五入模式四舍五入，除非两个邻边距离相等

public static void main(String[] args) {
        BigDecimal a = new BigDecimal(-0.35);
        BigDecimal b = new BigDecimal(1);
        BigDecimal c = a.divide(b,1,BigDecimal.ROUND_HALF_DOWN );
        LOGGER.error("原值：-0.35///"+c.toString()+"=-0.3");
        //结论：正负数相同，以5为分界，<=5舍掉，>5的进1
    }

　　7.ROUND_HALF_EVEN 四舍五入的方式是四舍五入，除非两个邻边是等距的，在这种情况下，四舍五入对甚至邻居。

public static void main(String[] args) {
        BigDecimal a = new BigDecimal(-0.35);
        BigDecimal b = new BigDecimal(1);
        BigDecimal c = a.divide(b,1,BigDecimal.ROUND_HALF_EVEN );
        LOGGER.error("原值：-0.35///"+c.toString()+"=-0.3");
        //结论：正负数相同，以5为分界，<=5舍掉，>5的进1
    }

　　8.ROUND_UNNECESSARY 舍入模式，以断言所请求的操作具有精确值结果，因此不需要舍入。

public static void main(String[] args) {
        BigDecimal a = new BigDecimal(-0.36);
        BigDecimal b = new BigDecimal(1);
        BigDecimal c = a.divide(b,1,BigDecimal.ROUND_HALF_EVEN );
        LOGGER.error("原值：-0.36///"+c.toString()+"=-0.4");
        //结论：正负数相同，以5为分界，<=5舍掉，>5的进1
        // 断言中使用的，实际开发过程中最好不用
    }

三：BigDecimal取值范围的 validation 校验问题总结

　　常常在与客户端交互时需要做很多校验，在javax.validation下面有很多不错的校验规则

　　

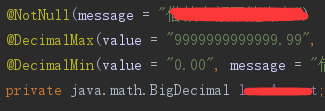
　　@NotNull ：不为空，适用任何地方（@NotBlank只是用字符类型）

　　@DecimalMax：取得最大值范围

　  @DecimalMin(value = "0.00", message = "") 取值最小值

三：BigDecimal精度科学计数法问题总结

　　BigDecimal有一种方法是：stripTrailingZeros()，它提供了去掉小数点后面的多余的0，但是问题是：

　　

    public static void main(String[] args) {
        BigDecimal A = BigDecimal.valueOf(0.36000).stripTrailingZeros();
        BigDecimal B = new BigDecimal(0.36000).stripTrailingZeros();
        BigDecimal zeroDecimal = new BigDecimal(0.000).stripTrailingZeros();
        System.out.println("原值0.36000//////"+A.toPlainString()+"===0.36");
        System.out.println("原值0.36000//////"+B.toPlainString()+"===35999999999999998667732370449812151491641998291015625");
        System.out.println("原值0.00000//////"+zeroDecimal+"==0.0000////"+zeroDecimal.toPlainString()+"==0");
    }

　　①：导出是excel会以科学计数法展示数据，如120 -》1.2+E2；

　　②：如果0.000然后用stripTrailingZeros()是无效的,导出时toPlainString（）加上之后就可以了；

　　③：慎用new BigDecimal();源代码如下；

/**这个构造函数的结果可能有些不可预测。
*可能会假设编写{@code new BigDecimal(0.1)}
* Java创建一个完全等于的{@code BigDecimal}
* 0.1(未缩放值为1，刻度为1)，但它是
*实际上等于 *0.1000000000000000055511151231257827021181583404541015*625.
**/

public BigDecimal(double val) {
        this(val,MathContext.UNLIMITED);
    }