Merkle Patricia Tree (MPT) 树详解

1.    介绍

　　

　　Merkle Patricia Tree(简称MPT树，实际上是一种trie前缀树)是以太坊中的一种加密认证的数据结构，可以用来存储所有的(key，value)对。以太坊区块的头部包括一个区块头，一个交易的列表和一个uncle区块的列表。在区块头部包括了交易的hash树根，用来校验交易的列表。在p2p网络上传输的交易是一个简单的列表，它们被组装成一个叫做trie树的特殊数据结构，来计算根hash。值得注意的是，除了校验区块外，这个数据结构并不是必须的，一旦区块被验证正确，那么它在技术上是可以忽略的。但是，这意味着交易列表在本地以trie树的形式存储，发送给客户端的时候序列化成列表。客户端接收到交易列表后重新构建交易列表trie树来验证根hash。RLP(Recursive length prefix encoding,递归长度前缀编码)，用来对trie树种所有的条目进行编码(参考：http://www.cnblogs.com/fengzhiwu/p/5565559.html)。

　　Trie树也叫作Radix树，为了提高效率，以太坊在实现上对其做了一些改进。在一般的radix树中，key是从树根到对应value得真实的路径。即从根节点开始，key中的每个字符会标识走那个子节点从而到达相应value。Value被存储在叶子节点，是每条路径的终止。假如key来自一个包含N个字符的字母表，那么树中的每个节点都可能会有多达N个孩子，树的最大深度是key的最大长度。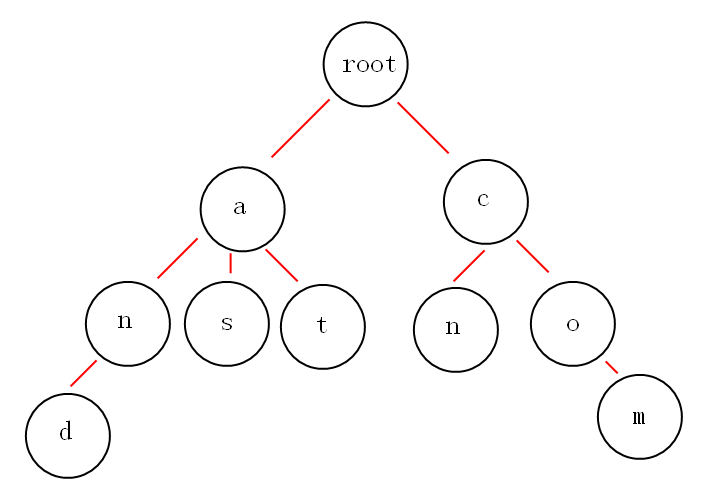

　　Radix的好处是具有相同前缀的key所对应的value在树中是非常靠近的，并且trie中不会有像hash-table一样的冲突。但是它也有缺陷，假如有一个很长的key，没有其他的key和它有公共的前缀，那么在遍历或存储它对应的值得时候，你就会遍历或存储相当多的节点，因为这棵树是非常不平衡的。

2.    特性

　　以太坊对Radix树的实现做了很多改进。

　　首先，为了保证树的加密安全，每个节点通过他的hash被引用，而非32bit或64bit的内存地址，即树的Merkle部分是一个节点的确定性加密的hash。一个非叶节点存储在leveldb关系型数据库中，数据库中的key是节点的RLP编码的sha3哈希，value是节点的RLP编码。代码中的实现如图：

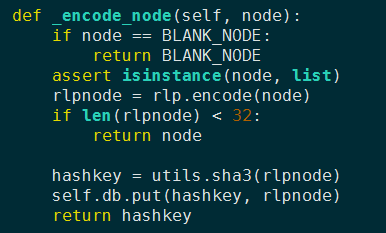
　　想要获得一个非叶节点的子节点，只需要根据子节点的hash访问数据库获得节点的RLP编码，然后解码就行了。如图所示：

　　

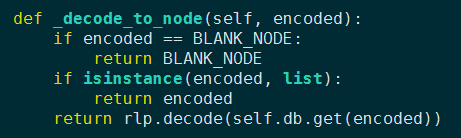
　　通过这种模式，根节点就成为了整个树的加密签名，如果一颗给定trie的跟hash是公开的，那么所有人都可以提供一种证明，通过提供每步向上的路径证明特定的key是否含有给定的值。

　　第二，引入了很多节点类型来提高效率。MPT树中的节点包括空节点、叶子节点、扩展节点和分支节点。

　　其中有空节点，简单的表示空，在代码中是一个空串。

　　标准的叶子节点，表示为[key,value]的一个list，其中key是key的一种特殊十六进制编码，value是value的RLP编码。

　　扩展节点，也是[key，value]的列表，但是这里的value是其他节点的hash，这个hash可以被用来查询数据库中的节点。也就是说通过hash链接到其他节点。

　　最后分支节点，因为MPT树中的key被编码成一种特殊的16进制的表示，再加上最后的value，所以分支节点是一个长度为17的list，前16个元素对应着key中的16个可能的十六进制字符，如果有一个[key,value]对在这个分支节点终止，最后一个元素代表一个值，即分支节点既可以搜索路径的终止也可以是路径的中间节点。

　　除了四种节点，MPT树中另外一个重要的概念是一个特殊的十六进制前缀(hex-prefix, HP)编码，用来对key进行编码。因为字母表是16进制的，所以每个节点可能有16个孩子。因为有两种[key,value]节点(叶节点和扩展节点)，引进一种特殊的终止符标识来标识key所对应的是值是真实的值，还是其他节点的hash。如果终止符标记被打开，那么key对应的是叶节点，对应的值是真实的value。如果终止符标记被关闭，那么值就是用于在数据块中查询对应的节点的hash。无论key奇数长度还是偶数长度，HP多可以对其进行编码。最后我们注意到一个单独的hex字符或者4bit二进制数字，即一个nibble。

　　HP编码很简单。一个nibble被加到key前，对终止符的状态和奇偶性进行编码。最低位表示奇偶性，第二低位编码终止符状态。如果key是偶数长度，那么加上另外一个nubble，值为0来保持整体的偶特性。

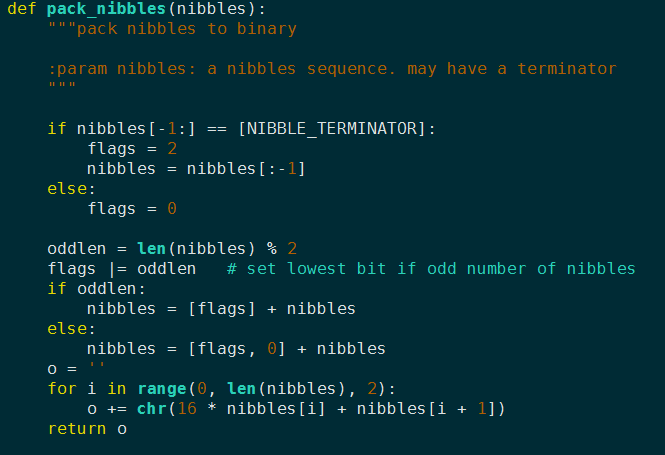
3.　　操作

　　下面从MPT树的更新，删除和查找过程来说明MPT树的操作。

• 更新

　　函数_update_and_delete_storage(self, node, key, value)

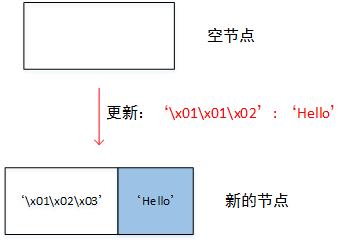
　　i. 如果node是空节点，直接返回[pack_nibbles(with_terminator(key)), value]，即对key加上终止符，然后进行HP编码。

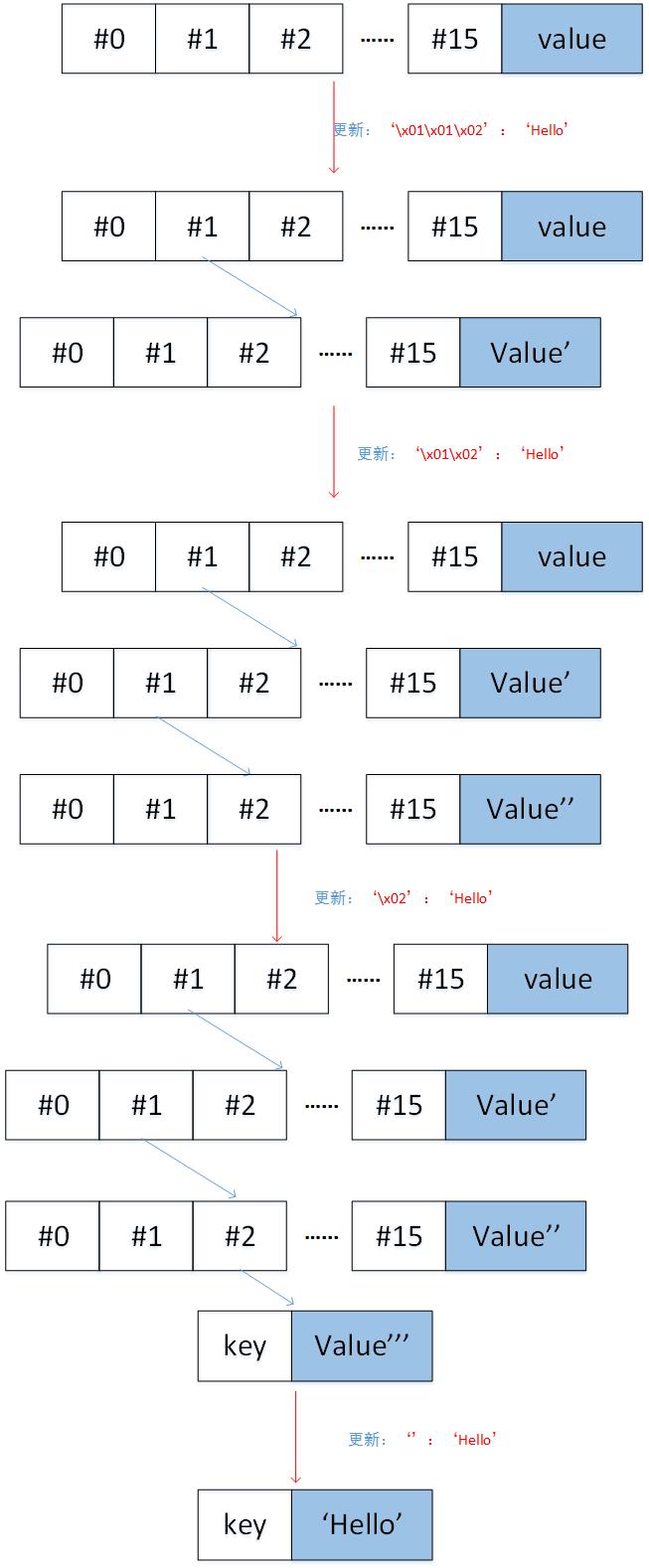
　　ii. 如果node是分支节点，如果key为空，则说明更新的是分支节点的value，直接将node[-1]设置成value就行了。如果key不为空，则递归更新以key[0]位置为根的子树，即沿着key往下找，即调用_update_and_delete_storage(self._decode_to_node(node[key[0]]), key[1:], value)。

　　iii. 如果node是kv节点（叶子节点或者扩展节点），调用_update_kv_node(self, node, key, value)，见步骤iv

　　iv. curr_key是node的key，找到curr_key和key的最长公共前缀，长度为prefix_length。Key剩余的部分为remain_key，curr_key剩余的部分为remain_curr_key。

　　　　a)    如果remain_key==[]== remain_curr_key，即key和curr_key相等，那么如果node是叶子节点，直接返回[node[0], value]。如果node是扩展节点，那么递归更新node所链接的子节点，即调用_update_and_delete_storage(self._decode_to_node(node[1]), remain_key, value)

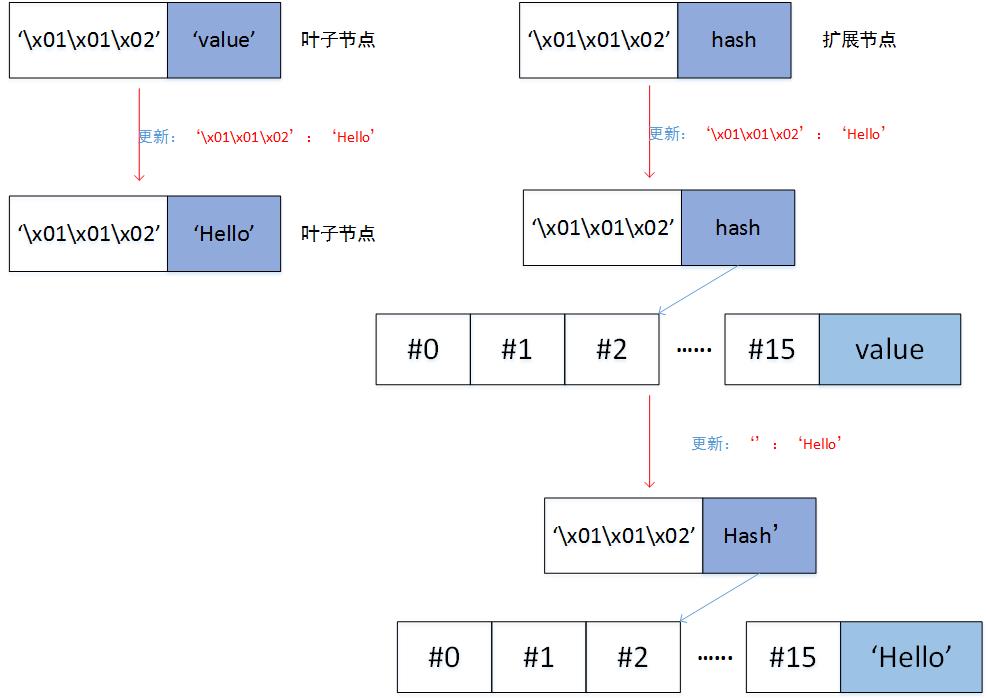
　　　　b)    如果remain_curr_key == []，即curr_key是key的一部分。如果node是扩展节点，递归更新node所链接的子节点，即调用_update_and_delete_storage(self._decode_to_node(node[1]), remain_key, value)；如果node是叶子节点，那么创建一个分支节点，分支节点的value是当前node的value，分支节点的remain_key[0]位置指向一个叶子节点，这个叶子节点是[pack_nibbles(with_terminator(remain_key[1:])), value]

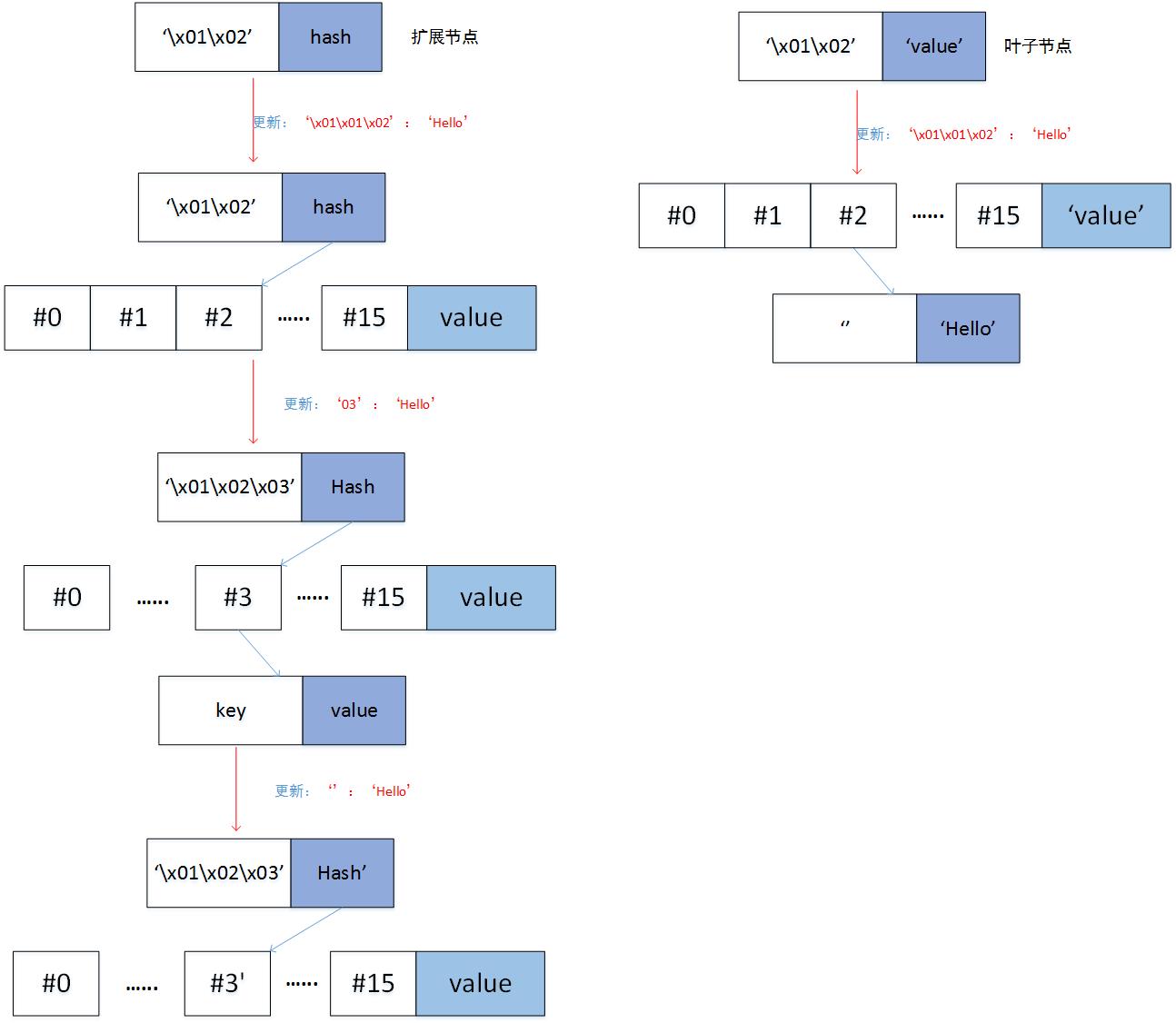
　　　　c)    否则，创建一个分支节点。如果curr_key只剩下了一个字符，并且node是扩展节点，那么这个分支节点的remain_curr_key[0]的分支是node[1]，即存储node的value。否则，这个分支节点的remain_curr_key[0]的分支指向一个新的节点，这个新的节点的key是remain_curr_key[1:]的HP编码，value是node[1]。如果remain_key为空，那么新的分支节点的value是要参数中的value，否则，新的分支节点的remain_key[0]的分支指向一个新的节点，这个新的节点是[pack_nibbles(with_terminator(remain_key[1:])), value]

　　　　d)    如果key和curr_key有公共部分，为公共部分创建一个扩展节点，此扩展节点的value链接到上面步骤创建的新节点，返回这个扩展节点；否则直接返回上面步骤创建的新节点

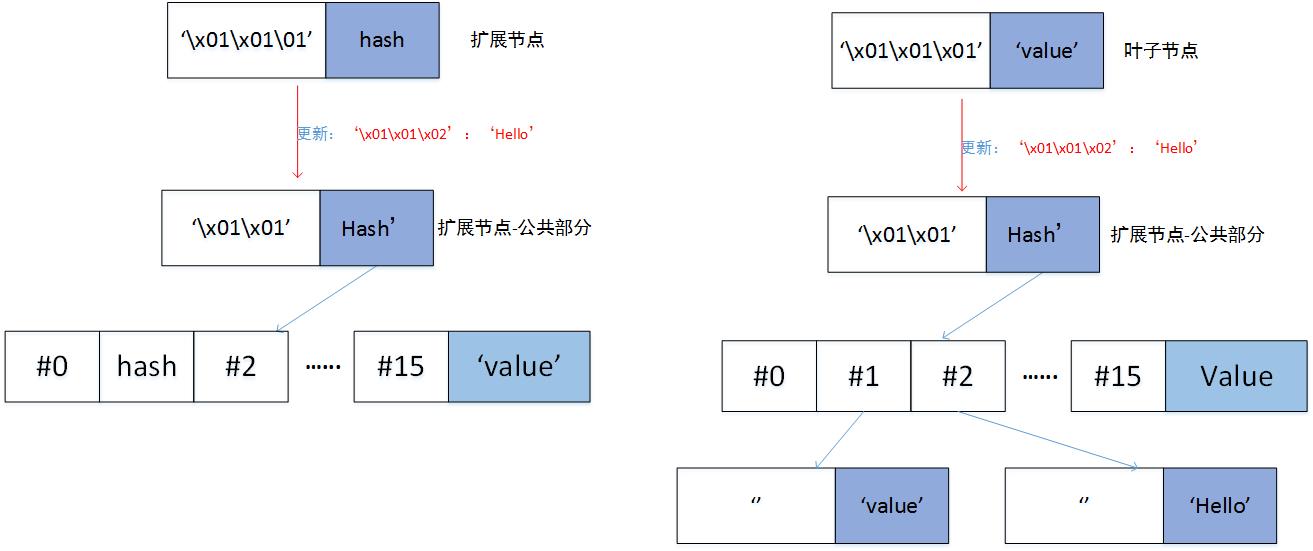
　　v. 删除老的node，返回新的node

• 删除

　　删除的过程和更新的过程类似，而且很简单，函数名：_delete_and_delete_storage(self, key)

　　i. 如果node为空节点，直接返回空节点

　　ii. 如果node为分支节点。如果key为空，表示删除分支节点的值，直接另node[-1]=‘’, 返回node的正规化的结果。如果key不为空，递归查找node的子节点，然后删除对应的value，即调用self._delete_and_delete_storage(self._decode_to_node(node[key[0]]), key[1:])。返回新节点

　　iii. 如果node为kv节点，curr_key是当前node的key。

　　　　a) 如果key不是以curr_key开头，说明key不在node为根的子树内，直接返回node。

　　　　b) 否则，如果node是叶节点，返回BLANK_NODE if key == curr_key else node。

　　　　c)如果node是扩展节点，递归删除node的子节点，即调用_delete_and_delete_storage(self._decode_to_node(node[1]), key[len(curr_key):])。如果新的子节点和node[-1]相等直接返回node。否则，如果新的子节点是kv节点，将curr_key与新子节点的可以串联当做key，新子节点的value当做vlaue，返回。如果新子节点是branch节点，node的value指向这个新子节点，返回。

• 查找

　　查找操作更简单，是一个递归查找的过程函数名为：_get(self, node, key)

　　i. 如果node是空节点，返回空节点

　　ii. 如果node是分支节点，如果key为空，返回分支节点的value；否则递归查找node的子节点，即调用_get(self._decode_to_node(node[key[0]]), key[1:])

　　iii. 如果node是叶子节点，返回node[1] if key == curr_key else ‘’

　　iv. 如果node是扩展节点，如果key以curr_key开头，递归查找node的子节点，即调用_get(self._decode_to_node(node[1]), key[len(curr_key):])；否则，说明key不在以node为根的子树里，返回空

4.    总结

　　相对于普通的前缀树，MPT树能有效减少Trie树的深度，增加Trie树的平衡性。而且通过节点的hash值进行树的节点的链接，有助于提高树的安全性和可验证性。所以说MPT树是Trie和Merkle树混合加上平衡操作后的产物。

参考：

https://easythereentropy.wordpress.com/2014/06/04/understanding-the-ethereum-trie/

https://github.com/ethereum/wiki/wiki/Patricia-Tree

https://github.com/ebuchman/understanding_ethereum_trie

https://github.com/ethereum/pyethereum