傅立叶级数是基于周期函数的，如果我们把周期推广到\infty

两者的频谱图对比，可以看到傅立叶变换的频谱图是连续的（上面是周期函数的傅立叶级数分解，下面是非周期函数的傅立叶变换）：

马同学高等数学

功率谱是信号自相关函数的傅里叶变换，能量谱是信号本身傅立叶变换幅度的平方

对于功率信号，常用功率谱来描述。所谓的功率谱，也称为功率谱密度。

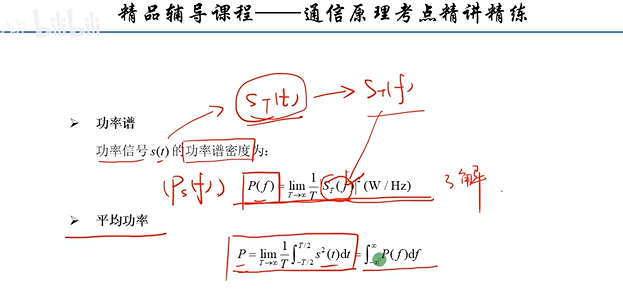
所以求功率谱就有了两种方法：1.(傅立叶变换的平方)/(区间长度)；2.自相关函数的傅里叶变换。这两种方法分别叫做直接法和相关函数法。

Ref：

如何通俗地理解傅立叶变换？

傅里叶级数和傅里叶变换是什么关系？

如果看了这篇文章你还不懂傅里叶变换，那就过来掐死我吧

【时间序列】PSD功率谱密度简介, PSD 功率谱密度 就是看每个频率上能量的大小

功率谱密度如何理解？

https://www.bilibili.com/video/BV1t54y1n7Lm?from=search&seid=12533754556719956566&spm_id_from=333.337.0.0

https://zhuanlan.zhihu.com/p/34989414

https://blog.csdn.net/u013457167/article/details/85805019

https://www.zhihu.com/question/39592966

https://www.researchgate.net/post/What-formula-should-I-use-to-calculate-the-power-spectrum-density-of-a-FFT, PSD 计算公式

 

傅里叶级数 傅里叶变换 FFT 时域 频域 功率谱 能量谱 功率谱密度PSD的更多相关文章

  1. 快速傅里叶变换FFT& 数论变换NTT

    相关知识 时间域上的函数f(t)经过傅里叶变换(Fourier Transform)变成频率域上的F(w),也就是用一些不同频率正弦曲线的加 权叠加得到时间域上的信号. \[ F(\omega)=\m ...

  2. 基于python的快速傅里叶变换FFT（二）

    基于python的快速傅里叶变换FFT(二)本文在上一篇博客的基础上进一步探究正弦函数及其FFT变换. 知识点  FFT变换,其实就是快速离散傅里叶变换,傅立叶变换是数字信号处理领域一种很重要的算法. ...

  3. 快速傅里叶变换FFT

    多项式乘法 #include <cstdio> #include <cmath> #include <algorithm> #include <cstdlib ...

  4. [学习笔记] 多项式与快速傅里叶变换(FFT)基础

    引入 可能有不少OIer都知道FFT这个神奇的算法, 通过一系列玄学的变化就可以在 $O(nlog(n))$ 的总时间复杂度内计算出两个向量的卷积, 而代码量却非常小. 博主一年半前曾经因COGS的一 ...

  5. 多项式 之 快速傅里叶变换(FFT)/数论变换(NTT)/常用套路【入门】

    原文链接https://www.cnblogs.com/zhouzhendong/p/Fast-Fourier-Transform.html 多项式 之 快速傅里叶变换(FFT)/数论变换(NTT)/ ...

  6. 快速傅里叶变换(FFT)

    扯 去北京学习的时候才系统的学习了一下卷积,当时整理了这个笔记的大部分.后来就一直放着忘了写完.直到今天都腊月二十八了,才想起来还有个FFT的笔记没整完呢.整理完这个我就假装今年的任务全都over了吧 ...

  7. 快速傅里叶变换(FFT)_转载

    FFTFFT·Fast  Fourier  TransformationFast  Fourier  Transformation快速傅立叶变换 P3803 [模板]多项式乘法(FFT) 参考上文 首 ...

  8. 浅谈范德蒙德(Vandermonde)方阵的逆矩阵的求法以及快速傅里叶变换(FFT)中IDFT的原理

    浅谈范德蒙德(Vandermonde)方阵的逆矩阵与拉格朗日(Lagrange)插值的关系以及快速傅里叶变换(FFT)中IDFT的原理 标签: 行列式 矩阵 线性代数 FFT 拉格朗日插值 只要稍微看 ...

  9. 快速傅里叶变换FFT / NTT

    目录 FFT 系数表示法 点值表示法 复数 DFT(离散傅里叶变换) 单位根的性质 FFT(快速傅里叶变换) IFFT(快速傅里叶逆变换) NTT 阶 原根 扩展知识 FFT 参考blog: 十分简明 ...

  10. 【学习笔记】快速傅里叶变换(FFT)

    [学习笔记]快速傅里叶变换 学习之前先看懂这个 浅谈范德蒙德(Vandermonde)方阵的逆矩阵的求法以及快速傅里叶变换(FFT)中IDFT的原理--gzy hhh开个玩笑. 讲一下\(FFT\) ...

随机推荐

  1. BootStrap Table 添加序列号

    js $('#table').bootstrapTable({ striped: true,//隔行换色 columns: [ { field: '', title: '序号', sortable: ...

  2. mybatis log4j打印sql语句

    依赖 <dependency> <groupId>org.slf4j</groupId> <artifactId>slf4j-log4j12</a ...

  3. Java Redis多限流

    Java Redis多限流 在Java中实现Redis多限流通常涉及使用Redis的某些特性,如INCR.EXPIRE.Lua脚本或者更高级的Redis数据结构如Redis Bitmaps.Redis ...

  4. 【VMware VCF】VMware Cloud Foundation Part 02：部署 Cloud Builder。

    VMware Cloud Builder 是用于构建 VMware Cloud Foundation 第一个管理域的自动化部署工具,通过将一个预定义信息的 Excel 参数表导入到 Cloud Bui ...

  5. CF30D King's Problem? 题解

    CF30D 题意 有 \(n+1\) 个点,其中的 \(n\) 个点在数轴上.求以点 \(k\) 为起点走过所有点的最短距离,允许重复. 思路 有两种情况: \(k\) 在数轴上(如图1). \(k\ ...

  6. OpenGL之ShadowMap

    流程:先创建一个RenderTexture,然后用灯光的视口渲染. 然后切换到正常相机,进行渲染,使用RenderTexture中的深度或者颜色纹理,然后还原当前顶点在灯光中的深度,两者对比,比缓存中 ...

  7. app专项测试：app弱网测试（测试工具）

    app专项测试:app弱网测试(测试工具) 除了常用的 fiddler,charles 可以模拟弱网,还有硬件工具弱网仪 HoloWAN也可以模拟弱网 使用弱网仪有以下优点:1.即插即用,无需调试和复 ...

  8. 【MySQL】主从配置

    一主一从(或二从)部署: 参考博客: https://www.cnblogs.com/lelehellow/p/9633315.html 正好借着3台机器,可以做一个 1主 2从的分配 192.168 ...

  9. 【Maxwell】01 安装及入门

    官网地址: https://maxwells-daemon.io/ 下载地址(版本发行): https://github.com/zendesk/maxwell/releases 参考教程自尚硅谷视频 ...

  10. “refer to”和“refer to as”在英语中的用法有所不同

    "refer to"和"refer to as"在英语中的用法有所不同,具体区别如下: Refer to "Refer to"意为" ...