系数矩阵为Hessian矩阵时使用“Pearlmutter trick”或“有限差分法”近似的共轭梯度解法 —— Hession-free的共轭梯度法

共轭梯度法已经在前文中给出介绍：

python版本的“共轭梯度法”算法代码

共轭梯度法用来求解方程A*x=b，且A为正定矩阵。

在机器学习领域很多优化模型的求解最终可以写为A*x=b的形式，且A为正定矩阵或A为近似矩阵。在凸优化问题中A为正定矩阵是比较好满足的，在神经网络这类非线性问题中一般常用近似的技术方法来获得近似正定矩阵的A，相关见：https://www.zhihu.com/question/268719846/answer/351360155

而很多时候A*x=b中的A为Hession矩阵，即函数 f 对向量 w 的二次求导，如果w的size比较大，比如为1000000，那么这个Hession矩阵A的维度为1000000*1000000，然而这个大小的A矩阵是难以存储在内存中的。但是通过对共轭梯度法具体步骤的了解可以知道，在共轭梯度法的具体求解过程中我们其实并不是直接需要这个矩阵A进行参与计算的，我们需要直接参与计算的是A*p，由于A为Hession矩阵，因此我们有两种近似的方法来计算A*p，一种叫做“Pearlmutter trick”，一种叫做“有限差分法”。

利用“Pearlmutter trick”或“有限差分法”  近似的共轭梯度法又被称作Hession-free的共轭梯度法。

=======================================

使用共轭梯度法时，如果系数矩阵为Hessian矩阵，那么我们可以使用Pearlmutter trick技术或“有限差分法”来减少计算过程中的内存消耗，加速计算。

使用Pearlmutter trick和“有限差分法”的共轭梯度解法可以参考论文：

Fast Exact Multiplication by the Hessian

论文地址：

https://www.bcl.hamilton.ie/~barak/papers/nc-hessian.pdf

由于原论文中内容较多，所以我们介绍Pearlmutter trick技术和“有限差分法”的共轭梯度解法建议看的资料为其他网文blog：

https://justindomke.wordpress.com/2009/01/17/hessian-vector-products/

=======================================

 

1. 利用Pearlmutter trick的共轭梯度法

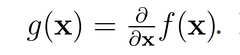
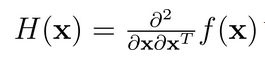
H(x)*p = ∂(g(x)*p)/∂x

=======================================

 

 

 

2. 利用有限差分法的共轭梯度法

 

 

依照上面内容解释一下：

Hession 矩阵 H(x) 为 f(x) 的二阶导数矩阵，因此有：

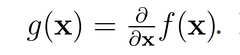
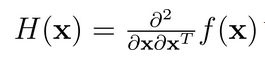
我们可以将  g(x)  按照泰勒公式展开为一阶导形式：

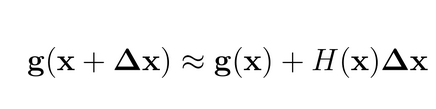
v 为一个向量vector，根据上面的公式我们可以得到：

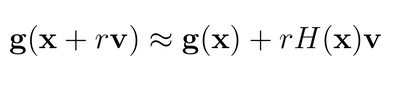
其中 γ 为标量系数，该系数极小，因此γv可以看做为Δx

因此我们可以得到下面形式的公式：

=======================================

 

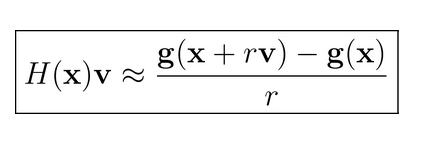
3. Pearlmutter trick技术和“有限差分法”的共轭梯度解法的 H(x)*p部分代码：

因为 H(x) 必然为正定对称矩阵，因此我们对  H(x) * y = b 形式的求解式可以使用共轭梯度法，而共轭梯度法在计算过程中需要重复的计算  H(x)*p， 其中 p 为计算过程中的迭代向量，p是在迭代过程中不断变化的，而H(x) 是系数矩阵在迭代过程中是不变的。

Pearlmutter trick 这个技术给出的是近似解，这里知道这个技术即可，实际感觉好像用处也不多，有可能是自己理解的不深。关于H(x)*b与共轭梯度的结合代码这里就省略掉了。

import torch

# 计算目标为： H*b,   H为函数s关于变量w的hessian矩阵
# 变量w
w = torch.randn(4, requires_grad=True)

# 关于变量w的函数s
data = torch.randn(1000*4).reshape((-1, 4))
label = torch.randn(1000)
s = torch.mean( torch.square(label - torch.matmul(data, w)) )

# 计算目标中的b
b = torch.randn(4)

# s对w的一阶导
first_grad = torch.autograd.grad(s, w, create_graph=True)[0]

# 使用标准公式计算 H*b
second_grad =  []
for grad in first_grad:
    second_grad.append(torch.autograd.grad(grad, w, retain_graph=True)[0][None, :])
H = torch.concatenate(second_grad, axis=0)
print("Hessian method:")
print(torch.matmul(H, b))

# 在目标函数s进行一阶导后点乘向量b, 然后再对w进行一次求导, 也就是 dot(first_grad, b)后再次求导
# 这样计算可以减少内存占用，因为该种计算方式不会在内存中对整个hessian矩阵进行展开
# 如果要重复计算 H*b，而b又每次迭代都变化的情况，此种方式的缺点是每次都需要再次求导,但是总计算量应该变化不大
tmp = torch.dot(first_grad, b)
print(torch.autograd.grad(tmp, w)[0])

# paper, Pearlmutter trick, 没太感觉出优势, 或许理解的不对
r = 0.0001
new_w = w+r*b
new_s = torch.mean( torch.square(label - torch.matmul(data, new_w)) )

new_first_grad = torch.autograd.grad(new_s, w)[0]
print( (new_first_grad - first_grad)/r )

注意：

这个代码一共输出三行，第一行是真实的 H(x)*b ，第二行是 Pearlmutter trick 技术计算的 H(x)*b，第三行是有限差分法计算的 H(x)*b 。