【单调栈 动态规划】bzoj1057: [ZJOI2007]棋盘制作

好像还有个名字叫做“极大化”？

Description

　　国际象棋是世界上最古老的博弈游戏之一，和中国的围棋、象棋以及日本的将棋同享盛名。据说国际象棋起源

于易经的思想，棋盘是一个8*8大小的黑白相间的方阵，对应八八六十四卦，黑白对应阴阳。而我们的主人公小Q，

正是国际象棋的狂热爱好者。作为一个顶尖高手，他已不满足于普通的棋盘与规则，于是他跟他的好朋友小W决定

将棋盘扩大以适应他们的新规则。小Q找到了一张由N*M个正方形的格子组成的矩形纸片，每个格子被涂有黑白两种

颜色之一。小Q想在这种纸中裁减一部分作为新棋盘，当然，他希望这个棋盘尽可能的大。不过小Q还没有决定是找

一个正方形的棋盘还是一个矩形的棋盘（当然，不管哪种，棋盘必须都黑白相间，即相邻的格子不同色），所以他

希望可以找到最大的正方形棋盘面积和最大的矩形棋盘面积，从而决定哪个更好一些。于是小Q找到了即将参加全

国信息学竞赛的你，你能帮助他么？

Input

　　第一行包含两个整数N和M，分别表示矩形纸片的长和宽。接下来的N行包含一个N * M的01矩阵，表示这张矩形

纸片的颜色（0表示白色，1表示黑色）。

Output

　　包含两行，每行包含一个整数。第一行为可以找到的最大正方形棋盘的面积，第二行为可以找到的最大矩形棋

盘的面积（注意正方形和矩形是可以相交或者包含的）。

Sample Input

3 3
1 0 1
0 1 0
1 0 0

Sample Output

4
6

HINT

N, M ≤ 2000

---

题目分析

第一步先插空把数字取反，把“黑白相间”这个条件转为求最大0/1矩形。

如果只是求最大的正方形，用dp非常容易解决。但因为这里还要求最大矩形，所以用单调栈会更加方便一些。

先预处理$s[i][j]$表示在第$i$行，以第$j$列为结束的0序列长度。

处理出这个东西以后，先固定一列$j$，再枚举每一行$i$。对于这个枚举出来的点$(i,j)$，就可以利用预处理出的$s[i][j]$来寻找它向上所能最大扩张长度。

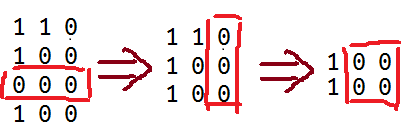
实际处理的过程如图所示。

另推荐一篇博客：https://blog.csdn.net/Tag_king/article/details/45166051

 #include<bits/stdc++.h>
 const int maxn = ;

 struct node
 {
     int x,h;
     node(int a=, int b=):x(a),h(b) {}
 }stk[maxn];
 int n,m,cnt;
 int squ,rect;
 int a[maxn][maxn],s[maxn][maxn];

 int read()
 {
     char ch = getchar();
     int num = ;
     bool fl = ;
     for (; !isdigit(ch); ch = getchar())
         if (ch=='-') fl = ;
     for (; isdigit(ch); ch = getchar())
         num = (num<<)+(num<<)+ch-;
     if (fl) num = -num;
     return num;
 }
 int sqr(int x){return x*x;}
 void push(int x, int h)
 {
     int now = x;
     while (cnt&&stk[cnt].h > h)
     {
         squ = std::max(squ, sqr(std::min(x-stk[cnt].x, stk[cnt].h)));
         rect = std::max(rect, (x-stk[cnt].x)*stk[cnt].h);
         now = stk[cnt].x;
         cnt--;
     }
     stk[++cnt] = node(now, h);
 }
 void calc()
 {
     for (int i=; i<=n; i++)
         for (int j=; j<=m; j++)
             s[i][j] = a[i][j]?:s[i][j-]+;
     for (int j=; j<=m; j++)
     {
         cnt = ;
         for (int i=; i<=n; i++) push(i, s[i][j]);
         push(n+, );
     }
 }
 int main()
 {
     n = read(), m = read();
     for (int i=; i<=n; i++)
         for (int j=; j<=m; j++)
             (i+j)%?a[i][j] = read():a[i][j] = -read();
     calc();
     for (int i=; i<=n; i++)
         for (int j=; j<=m; j++)
             a[i][j] = -a[i][j];
     calc();
     printf("%d\n%d\n",squ,rect);
     return ;
 }

END